标签:算法 == image out 说明 play com clu 三角形
参考书籍《算法设计与分析》 王晓东
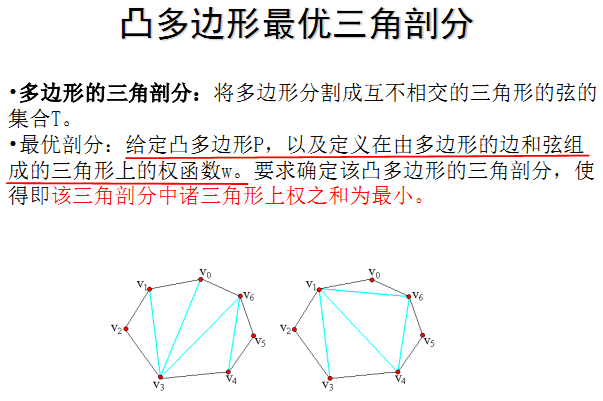
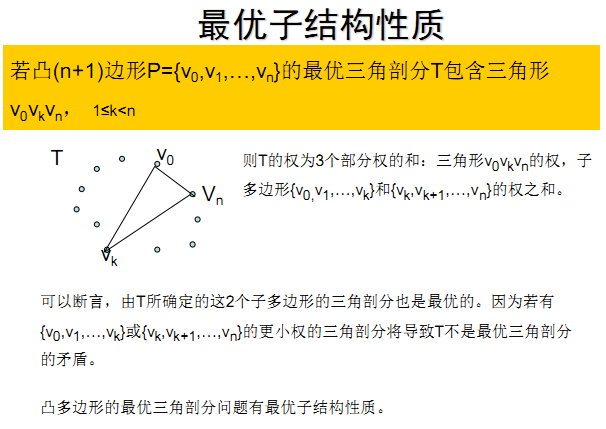
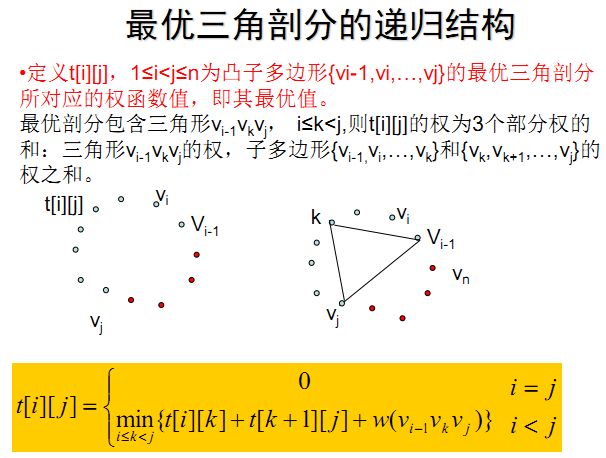

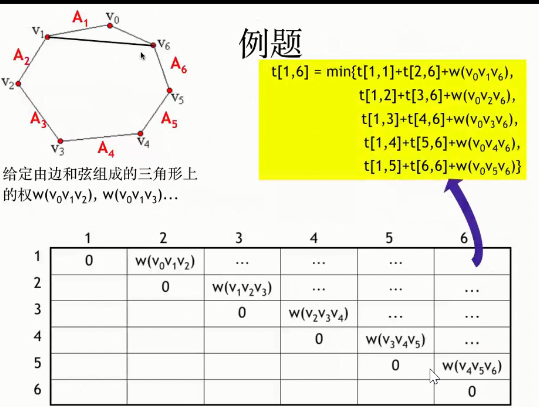
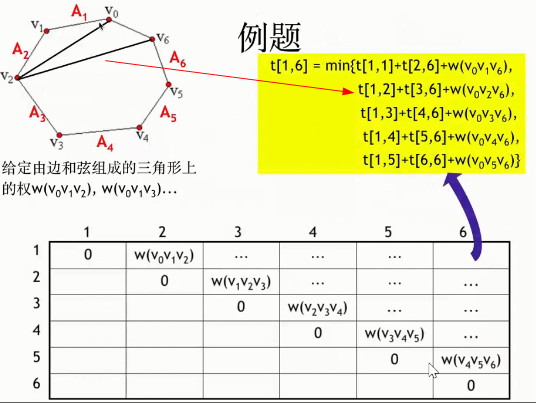
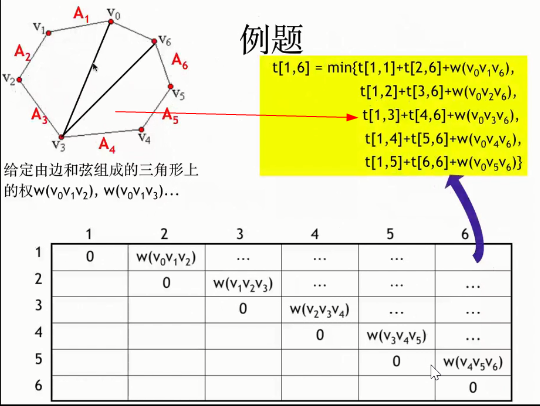
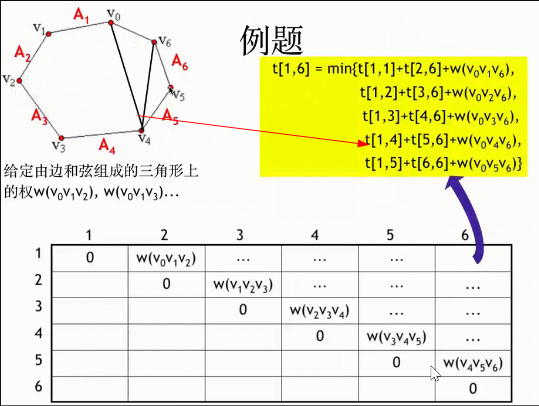
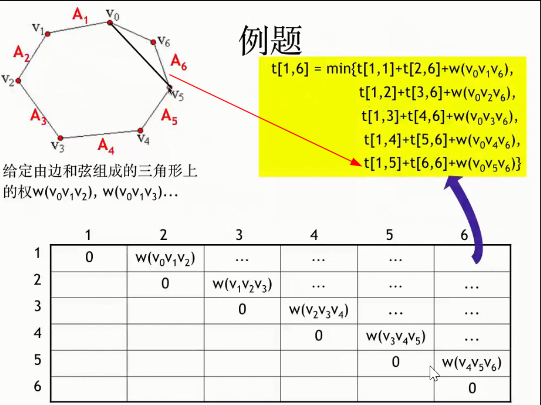
可以发现,这个过程和矩阵连乘最优计算次序问题极为相似。矩阵连乘的最优计算次序问题等价于矩阵链的最优完全加括号方式。下图为5个矩阵连乘问题求解步骤
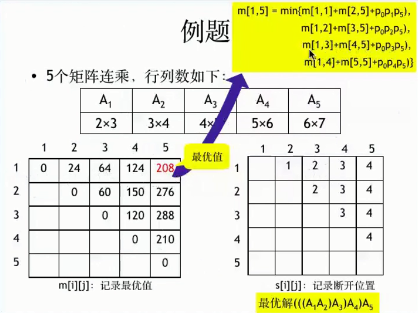
总结:

代码实现如下:

//3d5 凸多边形最优三角剖分 #include "stdafx.h" #include <iostream> using namespace std; const int N = 7;//凸多边形边数+1 int weight[][N] = {{0,2,2,3,1,4},{2,0,1,5,2,3},{2,1,0,2,1,4},{3,5,2,0,6,2},{1,2,1,6,0,1},{4,3,4,2,1,0}};//凸多边形的权 int MinWeightTriangulation(int n,int **t,int **s); void Traceback(int i,int j,int **s);//构造最优解 int Weight(int a,int b,int c);//权函数 int main() { int **s = new int *[N]; int **t = new int *[N]; for(int i=0;i<N;i++) { s[i] = new int[N]; t[i] = new int[N]; } cout<<"此多边形的最优三角剖分值为:"<<MinWeightTriangulation(N-1,t,s)<<endl; cout<<"最优三角剖分结构为:"<<endl; Traceback(1,5,s); //s[i][j]记录了Vi-1和Vj构成三角形的第3个顶点的位置 return 0; } int MinWeightTriangulation(int n,int **t,int **s) { for(int i=1; i<=n; i++) { t[i][i] = 0; } for(int r=2; r<=n; r++) //r为当前计算的链长(子问题规模) { for(int i=1; i<=n-r+1; i++)//n-r+1为最后一个r链的前边界 { int j = i+r-1;//计算前边界为r,链长为r的链的后边界 t[i][j] = t[i+1][j] + Weight(i-1,i,j);//将链ij划分为A(i) * ( A[i+1:j] )这里实际上就是k=i s[i][j] = i; for(int k=i+1; k<j; k++) { //将链ij划分为( A[i:k] )* (A[k+1:j]) int u = t[i][k] + t[k+1][j] + Weight(i-1,k,j); if(u<t[i][j]) { t[i][j] = u; s[i][j] = k; } } } } return t[1][N-2]; } void Traceback(int i,int j,int **s) { if(i==j) return; Traceback(i,s[i][j],s); Traceback(s[i][j]+1,j,s); cout<<"三角剖分顶点:V"<<i-1<<",V"<<j<<",V"<<s[i][j]<<endl; } int Weight(int a,int b,int c) { return weight[a][b] + weight[b][c] + weight[a][c]; }
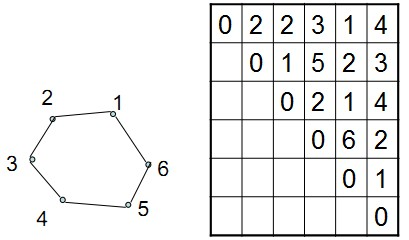
程序输入如下所示:
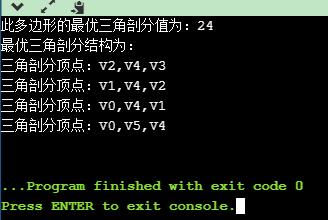
运行结果如下:
参考文献:王晓东《计算机设计与分析》
标签:算法 == image out 说明 play com clu 三角形
原文地址:https://www.cnblogs.com/cy0628/p/13944726.html