标签:lse 如何 今天 for char turn builder 解决问题 方案
漫画:如何实现大整数相乘?(下)如何用程序实现大整数相乘呢?
在上一篇文章 漫画:如何实现大整数相乘?(上) 修订版 当中,我们介绍了两种思路:
1.像列竖式一样,把两整数按位依次相乘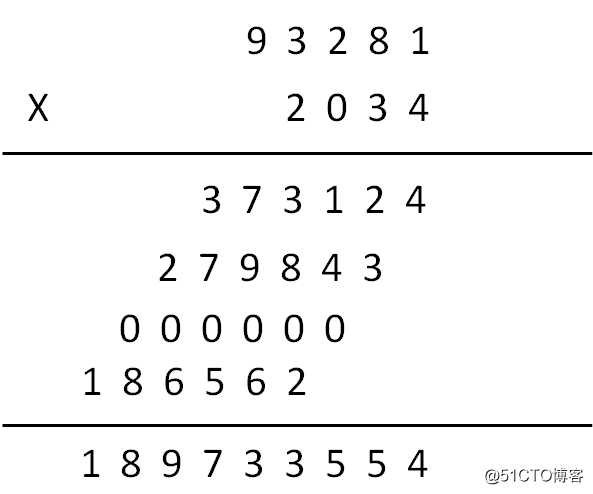
这个思路的时间复杂度是O(n^2)。
2.利用分治法,把每个大整数分成高位和低位两部分,转化成四个较小的乘积。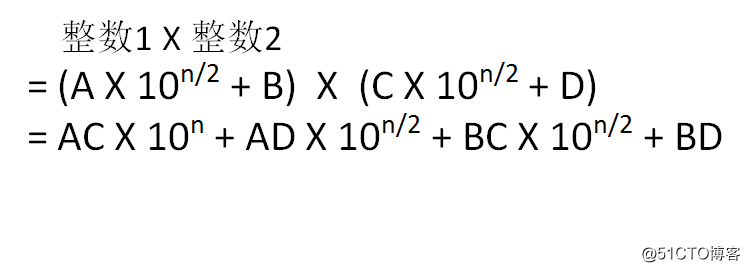
这个思路的时间复杂度同样是O(n^2)。
那么,有什么样的优化方案,可以使时间复杂度优于O(n^2)呢?我们今天一起来研究下。



如何做调整呢?其实很简单,连小学生都会:
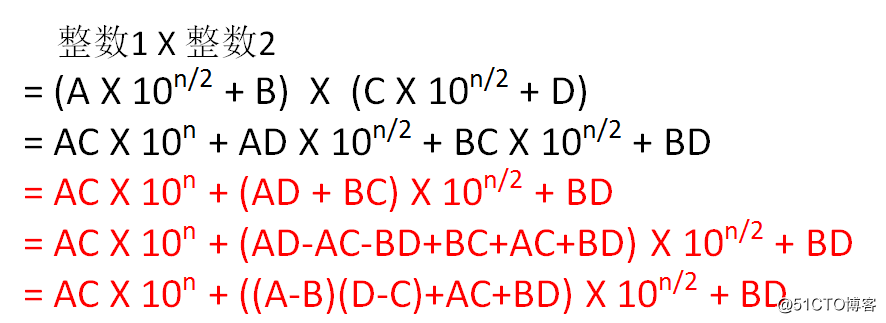
这样一来,原本的4次乘法和3次加法,转变成了3次乘法和6次加法。

这样一来,时间复杂度是多少呢?
假设两个长度为n的大整数相乘,整体运算规模是T(n) 。
刚才我们说过,两个大整数相乘可以被拆分成三个较小的乘积,
所以在第一次分治时,T(n)和T(n/2)有如下关系:
T(n) = 3T(n/2) + f(n)
其中f(n)是6次加法的运算规模,f(n)的渐进时间复杂度很明显是O(n)。
此时让我们回顾一下master定理:
设常数a >= 1,b > 1,如果一个算法的整体计算规模 T(n) = a T(n / b) + f(n),那么则有如下规律:
对于T(n) = 3T(n/2) + f(n)这个关系式来说, a=3, b=2。
把a和b的值,以及f(n)的时间复杂度带入到master定理的第一个规律,也就是下面的规律:
发现正好符合条件。
怎么符合条件呢?推导过程如下: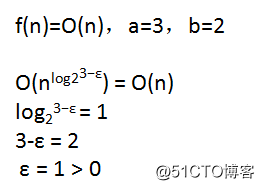
所以我们的平均时间复杂度是: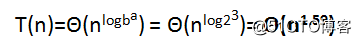
2 和 1.59 之间的差距看似不大,但是当整数长度非常大的时候,两种方法的性能将是天壤之别。


下面展示一下实现代码。我们的代码非常复杂,在这里只作为参考,最重要的还是解决问题的思路:
· · * 大整数乘法
· · * @param bigNumberA ?大整数A
· · * @param bigNumberB ?大整数B
· · */
· · public static String bigNumberMultiply(String bigNumberA, String bigNumberB) {
· · ? ?boolean isNegative = false;
· · ? ?if ((bigNumberA.startsWith("-") && bigNumberB.startsWith("-"))
· · ? ? ? ? ? ?|| (!bigNumberA.startsWith("-") && !bigNumberB.startsWith("-"))) {
· · ? ? ? ?// 两数同符号的情况
· · ? ? ? ?bigNumberA = bigNumberA.replaceAll("-", "");
· · ? ? ? ?bigNumberB = bigNumberB.replaceAll("-", "");
· · ? ?} else if ((bigNumberA.startsWith("-") && !bigNumberB.startsWith("-"))
· · ? ? ? ? ? ?|| (!bigNumberA.startsWith("-") && bigNumberB.startsWith("-"))) {
· · ? ? ? ?// 两数不同符号的情况
· · ? ? ? ?bigNumberA = bigNumberA.replace("-", "");
· · ? ? ? ?bigNumberB = bigNumberB.replace("-", "");
· · ? ? ? ?isNegative = true;
· · ? ?}
· · ? ?// 如果两数长度之和小于10,直接相乘返回
· · ? ?if (bigNumberA.length() + bigNumberB.length() < 10) {
· · ? ? ? ?// 计算乘积
· · ? ? ? ?int tmp = (Integer.parseInt(bigNumberA) * Integer.parseInt(bigNumberB));
· · ? ? ? ?if (tmp == 0) {
· · ? ? ? ? ? ?return "0";
· · ? ? ? ?}
· · ? ? ? ?String value = String.valueOf(tmp);
· · ? ? ? ?if(isNegative){
· · ? ? ? ? ? ?value = "-" + value;
· · ? ? ? ?}
· · ? ? ? ?return value;
· · ? ?}
· · ? ?// 公式 AC * 10^n+((A-B)(D-C)+AC+BD) * 10^(n/2)+BD当中的a,b,c,d
?String a, b, c, d;
· · ? ?if (bigNumberA.length() == 1) {
· · ? ? ? ?a = "0";
· · ? ? ? ?b = bigNumberA;
· · ? ?} else {
· · ? ? ? ?if (bigNumberA.length() % 2 != 0) {
· · ? ? ? ? ? ?bigNumberA = "0" + bigNumberA;
· · ? ? ? ?}
· · ? ? ? ?a = bigNumberA.substring(0, bigNumberA.length() / 2);
· · ? ? ? ?b = bigNumberA.substring(bigNumberA.length() / 2);
· · ? ?}
· · ? ?if (bigNumberB.length() == 1) {
· · ? ? ? ?c = "0";
· · ? ? ? ?d = bigNumberB;
· · ? ?} else {
· · ? ? ? ?if (bigNumberB.length() % 2 != 0) {
· · ? ? ? ? ? ?bigNumberB = "0" + bigNumberB;
· · ? ? ? ?}
· · ? ? ? ?c = bigNumberB.substring(0, bigNumberB.length() / 2);
· · ? ? ? ?d = bigNumberB.substring(bigNumberB.length() / 2);
· · ? ?}
· · ? ?// 按最大位数取值,以确定补零数目
· · ? ?int n = bigNumberA.length() >= bigNumberB.length() ? bigNumberA.length() : bigNumberB.length();
· ·
· · ? ?//t1,t2为中间运算结果,t3为乘法运算完毕的结果
· · ? ?String t1, t2, t3;
· · ? ?String ac = bigNumberMultiply(a, c);
· · ? ?String bd = bigNumberMultiply(b, d);
· ·
· · ? ?//t1=(A-B)(D-C)
· · ? ?t1 = bigNumberMultiply(bigNumberSubtract(a, b), bigNumberSubtract(d, c));
· · ? ?//t2=(A-B)(D-C)+AC+BD
· · ? ?t2 = bigNumberSum(bigNumberSum(t1, ac), bd);
· · ? ?//t3= AC * 10^n+((A-B)(D-C)+AC+BD) * 10^(n/2)+BD
· · ? ?t3 = bigNumberSum(bigNumberSum(Power10(ac, n), Power10(t2, n/2)), bd).replaceAll("^0+", "");
· · ? ?if (t3 == "")
· · ? ? ? ?return "0";
· · ? ?if(isNegative){
· · ? ? ? ?return "-" + t3;
· · ? ?}
· · ? ?return t3;
}
· ·
· ·
· ·
· · /**
· · * 大整数加法
· · * @param bigNumberA ?大整数A
· · * @param bigNumberB ?大整数B
· · */
· · public static String bigNumberSum(String bigNumberA, String bigNumberB) {
· ·
· · ? ?if (bigNumberA.startsWith("-") && !bigNumberB.startsWith("-")) {
· · ? ? ? ?return bigNumberSubtract(bigNumberB, bigNumberA.replaceAll("^-", ""));
· · ? ?} else if (!bigNumberA.startsWith("-") && bigNumberB.startsWith("-")) {
· · ? ? ? ?return bigNumberSubtract(bigNumberA, bigNumberB.replaceAll("^-", ""));
· · ? ?} else if (bigNumberA.startsWith("-") && bigNumberB.startsWith("-")) {
· · ? ? ? ?return "-" + bigNumberSum(bigNumberA.replaceAll("^-", ""), bigNumberB.replaceAll("^-", ""));
· · ? ?}
· ·
· · ? ?//1.把两个大整数用数组逆序存储,数组长度等于较大整数位数+1
· · ? ?int maxLength = bigNumberA.length() > bigNumberB.length() ? bigNumberA.length() : bigNumberB.length();
· · ? ?int[] arrayA = new int[maxLength+1];
· · ? ?for(int i=0; i< bigNumberA.length(); i++){
· · ? ? ? ?arrayA[i] = bigNumberA.charAt(bigNumberA.length()-1-i) - ‘0‘;
· · ? ?}
· · ? ?int[] arrayB = new int[maxLength+1];
· · ? ?for(int i=0; i< bigNumberB.length(); i++){
· · ? ? ? ?arrayB[i] = bigNumberB.charAt(bigNumberB.length()-1-i) - ‘0‘;
? ?}
? ?//2.构建result数组,数组长度等于较大整数位数+1
int[] result = new int[maxLength+1];
? ?//3.遍历数组,按位相加
?for(int i=0; i<result.length; i++){
? ? ? ?int temp = result[i];
? ? ?temp += arrayA[i];
? ? ? ?temp += arrayB[i];
? ? ? ?//判断是否进位
? ? ? ?if(temp >= 10){
? ? ? ? ? ?temp -= 10;
? ? ? ? ? ?result[i+1] = 1;
? ? ? ?}
? ? ? ?result[i] = temp;
? ?}
? ?//4.把result数组再次逆序并转成String
? ?StringBuilder sb = new StringBuilder();
? ?//是否找到大整数的最高有效位
? ?boolean findFirst = false;
? ? ? ?if(!findFirst){
? ? ? ? ? ?if(result[i] == 0){
? ? ? ? ? ? ? ?continue;
? ? ? ? ? ?findFirst = true;
? ? ? ?}
? ? ? ?sb.append(result[i]);
?}
? ?return sb.toString();
}
/**
* 大整数减法
* @param bigNumberA ?大整数A
* @param bigNumberB ?大整数B
*/
public static String bigNumberSubtract(String bigNumberA, String bigNumberB) {
?int compareResult = compare(bigNumberA, bigNumberB);
? ?if (compareResult == 0) {
? ? ? ?return "0";
? ?}
? ?boolean isNegative = false;
? ?if (compareResult == -1) {
? ? ? ?String tmp = bigNumberB;
? ? ? ?bigNumberB = bigNumberA;
? ? ? ?bigNumberA = tmp;
? ? ? ?isNegative = true;
? ?}
? ?//1.把两个大整数用数组逆序存储,数组长度等于较大整数位数+1
? ?int maxLength = bigNumberA.length() > bigNumberB.length() ? bigNumberA.length() : bigNumberB.length();
? ?int[] arrayA = new int[maxLength+1];
? ?for(int i=0; i< bigNumberA.length(); i++){
? ? ? ?arrayA[i] = bigNumberA.charAt(bigNumberA.length()-1-i) - ‘0‘;
? ?}
? ?int[] arrayB = new int[maxLength+1];
? ?for(int i=0; i< bigNumberB.length(); i++){
? ? ? ?arrayB[i] = bigNumberB.charAt(bigNumberB.length()-1-i) - ‘0‘;
? ?}
? ?//2.构建result数组,数组长度等于较大整数位数+1
? ?int[] result = new int[maxLength+1];
? ?//3.遍历数组,按位相加
? ?for(int i=0; i<result.length; i++){
? ? ? ?int temp = result[i];
? ? ? ?temp += arrayA[i];
? ? ? ?temp -= arrayB[i];
? ? ? ?//判断是否进位
? ? ? ?if(temp < 0){
? ? ? ? ? ?temp += 10;
? ? ? ? ? ?result[i+1] = -1;
? ? ? ?}
? ? ? ?result[i] = temp;
? ?}
? ?//4.把result数组再次逆序并转成String
? ?StringBuilder sb = new StringBuilder();
? ?//是否找到大整数的最高有效位
? ?boolean findFirst = false;
? ?for (int i = result.length - 1; i >= 0; i--) {
? ? ? ?if(!findFirst){
? ? ? ? ? ?if(result[i] == 0){
? ? ? ? ? ? ? ?continue;
? ? ? ? ? ?}
? ? ? ? ? ?findFirst = true;
? ? ? ?}
? ? ? ?sb.append(result[i]);
? ?}
? ?String value = sb.toString();
? ?if (isNegative) {
? ? ? ?value = "-" + value;
? ?}
? ?return value;
}
// 比较大小
private static int compare(String x, String y) {
? ?if (x.length() > y.length()) {
? ? ? ?return 1;
? ?} else if (x.length() < y.length()) {
? ? ? ?return -1;
? ?} else {
? ? ? ? ? ?if (x.charAt(i) > y.charAt(i)) {
? ? ? ? ? ? ? ?return 1;
? ? ? ? ? ?} else if (x.charAt(i) < y.charAt(i)) {
? ? ? ? ? ? ? ?return -1;
? ? ? ? ? ?}
? ? ? ?}
? ? ? ?return 0;
? ?}
}
// 扩大10的n次方倍
public static String Power10(String num, int n) {
? ?for (int i = 0; i < n; i++) {
? ? ? ?num += "0";
? ?return num;
}
public static void main(String[] args) {
? ?String x = "1513143";
? ?String y = "9345963";
? ?System.out.println(bigNumberMultiply(x, y));
}
? 需要注意的是,这段实现代码只适用于两个大整数长度相等的情况。如果想求解长度不等的整数相乘,只需要对代码做微小的改动,有兴趣的小伙伴没有试一试。



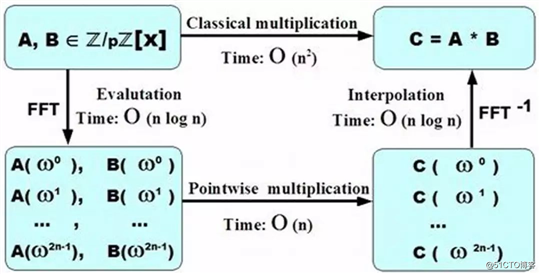

几点补充:
—————END—————
喜欢本文的朋友们,欢迎长按下图关注订阅号程序员小灰,收看更多精彩内容
标签:lse 如何 今天 for char turn builder 解决问题 方案
原文地址:https://blog.51cto.com/14982143/2550309