初中|数学题目整理

标签：如图所示   ram   绝对值   pad   log   math   图形   剖析   案例   

前言

典例剖析

已知\((x+y-3)^2+3|x-y-1|=0\)，求\(2x+y\)的值；

• 在初中阶段，常用的非负式子有二次式，二次根式，绝对值式；其实也就是分别考查\(y=x^2\geqslant 0\)，\(y=\sqrt{x}\geqslant 0\)，\(y=|x|\geqslant 0\)的非负性的应用，

分析：由于\((x+y-3)^2+3|x-y-1|=0\)，

且\((x+y-3)^2\geqslant 0\)，\(3|x-y-1|\geqslant 0\)，

则须满足条件\(\left\{\begin{array}{l}{x+y-3=0}\\{x-y-1=0}\end{array}\right.\)，

从而求得\(x=2\)，\(y=1\)，则\(2x+y=5\)；

变式1：已知\((x+y-3)^2+3(x-y-1)^2=0\)，求\(2x+y\)的值；

变式2：已知\(|x+y-3|+3|x-y-1|=0\)，求\(2x+y\)的值；

变式3：已知\((x+y-3)^2+\sqrt{x-y-1}=0\)，求\(2x+y\)的值；

变式4：已知\(\sqrt{x+y-3}+\sqrt{x-y-1}=0\)，求\(2x+y\)的值；

变式5：已知\(\sqrt{x+y-3}+3|x-y-1|=0\)，求\(2x+y\)的值；

变式6：已知\(|a-7|+\sqrt{b-24}+(c-25)^2=0\)，求以\(a,b,c\)为三边的三角形面积。

提示：\(7,24,25\)为勾股数，三角形为\(Rt\triangle\)，\(S=84\)；

说明：以上5个引申题目的求解过程和案例题目的求解过程完全相同；

[平面几何]如图，在\(Rt\triangle ABC\)中，\(\angle ACB=90^{\circ}\)，\(AC=3\)，\(BC=4\)，点\(D\)在\(AB\)上，\(AD=AC\)，\(AF\perp CD\)交\(CD\)于点\(E\)，交\(CB\)于点\(F\)，则\(CF\)的长为【】

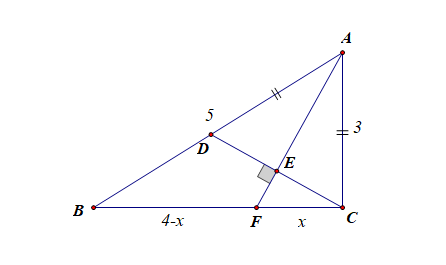
分析：容易知道，\(AB=5\)，在\(Rt\triangle ADE\)和\(Rt\triangle ACE\)中，由\(HL\)定理可知，\(\triangle ADE\cong \triangle ACE\)

故\(\angle DAE=\angle CAE\)，即\(AF\)为角\(A\)的角平分线，设\(CF=x\)，则\(FB=4-x\)

则由角平分线定理可知，\(\cfrac{AC}{AB}=\cfrac{CF}{FB}\)，即\(\cfrac{3}{5}=\cfrac{x}{4-x}\)，

解得\(x=1.5\)，故选\(A\)。

[平面几何]如图，正方形\(ABDE\)，\(CDFI\)，\(EFGH\)的面积分别为\(25\)，\(9\)，\(16\)，\(\triangle AEH\)，\(\triangle BDC\)，\(\triangle GFI\)的面积分别是\(S_1\)，\(S_2\)，\(S_3\)，则\(S_1+S_2+S_3\)的值为________。

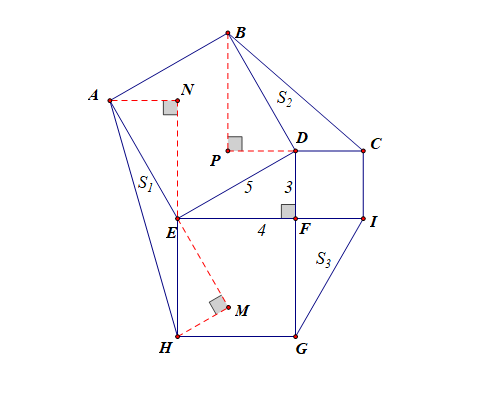
分析：做出如图所示的辅助线，由\(\angle PDE\)的两个余角分别为\(\angle EDF\)和\(\angle BDP\)，故\(\angle EDF=\angle BDP\)，

故\(\triangle EDF\sim\triangle BDP\)，又由于斜边\(BD=BE\)，故\(\triangle EDF\cong\triangle BDP\)，

同理可证，\(\triangle EDF\cong\triangle EAN\)，

或者理解为将\(Rt\triangle EDF\)绕点\(D\)顺时针旋转\(90^{\circ}\)得到\(Rt\triangle BDP\)，

将\(Rt\triangle EDF\)绕点\(E\)逆时针旋转\(90^{\circ}\)得到\(Rt\triangle EAN\)，

这样\(S_2=S_{\triangle BCP}-S_{\triangle BDP}=\cfrac{1}{2}\times 4\times(3+3)-\cfrac{1}{2}\times 4\times 3=6\)；

\(S_1=S_{\triangle AHN}-S_{\triangle EAN}=\cfrac{1}{2}\times 3\times(4+4)-\cfrac{1}{2}\times 4\times 3=6\)；

又\(S_3=\cfrac{1}{2}\times 3\times 4=6\)；故\(S_1+S_2+S_3=18\)；

已知整数\(X\)，\(Y\)满足条件\(\sqrt{X}+2\sqrt{Y}=\sqrt{72}\)，那么整数对\((X，Y)\)的个数为【】

法1：注意到题目的结构特征，\(\sqrt{X}\geqslant 0\)，则可知\(0\leqslant Y\leqslant 18\)，又\(Y\in N\)，

故可以让\(Y=0，1，\cdots ，18\)依次尝试，

\(Y=0\)时，\(X=72\)；\(Y=2\)时，\(X=32\)；\(Y=8\)时，\(X=8\)；\(Y=18\)时，\(X=0\)；

从而可以得到以下满足题意的整数对，\((0,18)\)；\((8,8)\)；\((32,2)\)；\((72,0)\)；故选\(C\)。

在\(\triangle ABC\)中，\(AB=13cm\)，\(AC=20cm\)，\(BC\)边上的高为\(12cm\)，则\(\triangle ABC\)的面积为__________。

分析：由题目的已知条件可以做出适合题意的两种图形如下所示，分别为锐角三角形和钝角三角形，

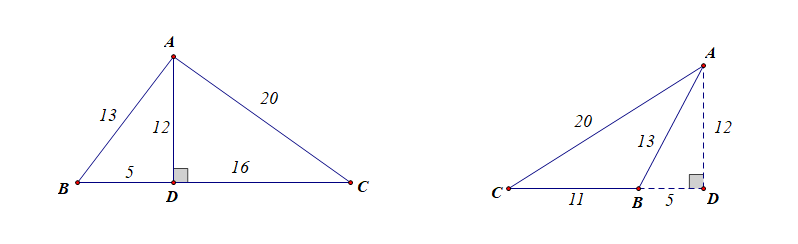
从而计算面积得到\(S_{\triangle ABC}=126cm^2\)或者\(S_{\triangle ABC}=66cm^2\)；

解后反思：本题目其实涉及到高中的三角形个数的判断，主要考查初中学生的分类讨论意识；

完全平方公式

勾股定理

初中|数学题目整理

标签：如图所示   ram   绝对值   pad   log   math   图形   剖析   案例   

原文地址：https://www.cnblogs.com/mathsonline/p/13947951.html