标签:break writer ref -o else and href 技术 pac
简单签到题。
code:
#include<bits/stdc++.h>
#define pi pair<int,int>
#define f first
#define s second
using namespace std;
const string mt[15]={"","Jan","Feb","Mar","Apr","May","Jun","Jul","Aug","Sept","Oct","Nov","Dec"};
int T,n;
pi dt[25],to;
map<string,int>mon;
void Getdate(pi&x){
string t;
char t1,t2;
cin>>t,x.f=mon[t];
scanf("%d%c%c",&x.s,&t1,&t2);
}
int main(){
mon["Jan"]=1;
mon["Feb"]=2;
mon["Mar"]=3;
mon["Apr"]=4;
mon["May"]=5;
mon["Jun"]=6;
mon["Jul"]=7;
mon["Aug"]=8;
mon["Sept"]=9;
mon["Oct"]=10;
mon["Nov"]=11;
mon["Dec"]=12;
scanf("%d",&T);
for(int fr=1;fr<=T;++fr){
scanf("%d",&n);
for(int i=1;i<=n;++i)Getdate(dt[i]);
Getdate(to),sort(dt+1,dt+n+1),printf("Case #%d: ",fr);
for(int i=1;i<=n;++i)if(dt[i].f>to.f||(dt[i].f==to.f&&dt[i].s>to.s)){
cout<<mt[dt[i].f]<<" ",printf("%d",dt[i].s);
if(dt[i].s==1||dt[i].s==21||dt[i].s==31)puts("st");
else if(dt[i].s==2||dt[i].s==22)puts("nd");
else if(dt[i].s==3||dt[i].s==23)puts("rd");
else puts("th");
goto Skip;
}
puts("See you next year");
Skip:;
}
return 0;
}
首先可以把所有不能到达\(1\)的点删掉。
然后考虑一条路径应该形如从\(0\)走到某个点,然后从这个点开始不停地走环,然后走到\(1\),或者直接从\(0\)走到\(1\)。
在点\(1\)上加一个边权为\(0\)的自环,就可以只考虑前者了。
然后每个点走出去的只能是所有出边中边权最小的,于是可以把其他边删掉。
我们可以通过确定这个小数的前若干位来得到最优解。可以发现如果两个长度分别为\(a\)和\(b\)的环权值不同,那么在\(a+b\)位之内就能比较出。对于一条链+一个环也有类似的结论。
因此我们只需要逐位确定前\(2n\)位即可。
考虑确定第\(i\)位时,记录走到哪些点可以在走了\(i-1\)步以后取到最小值,然后从这些点往后走即可。
然后考虑如何确定小数的循环节。我们可以枚举最后走到的点,从最后走到的点开始往回走(这需要我们在逐位确定时记录某个点是从哪个点走来的),如果这个点在往回走的路径上出现了大于等于\(2\)次(不算开始),并且两次出现之间的路径是一样的,我们就确定了循环节。
时间复杂度\(O(n^2)\)
code:
#include<bits/stdc++.h>
#define ci const int&
#define clr(vec) (vector<int>().swap(vec))
using namespace std;
const int mod=1e9+7;
struct edge{
int t,nxt;
}e[4010];
int T,n,m,u[4010],v[4010],w[4010],cn[2010],be[2010],cnt,tv[2010],li[2010],TIM,ans[4050],ls[2010][4050],nw,mn,p,stp,prt,v1,v2,ap,ti,tg,ar[2][4050],sz[2],l1,dl;
vector<int>to[2010],ae[2];
int POW(int x,int y){
int ret=1;
while(y)y&1?ret=1ll*ret*x%mod:0,x=1ll*x*x%mod,y>>=1;
return ret;
}
void add(ci x,ci y){
e[++cnt]=(edge){y,be[x]},be[x]=cnt;
}
void dfs(ci x){
cn[x]=1;
for(int i=be[x];i;i=e[i].nxt)if(!cn[e[i].t])dfs(e[i].t);
}
int main(){
scanf("%d",&T);
for(int fr=1;fr<=T;++fr){
scanf("%d%d",&n,&m),cnt=nw=0;
for(int i=1;i<=n;++i)cn[i]=be[i]=li[i]=prt=v1=0,tv[i]=10;
for(int i=1;i<=m;++i)scanf("%d%d%d",&u[i],&v[i],&w[i]),++u[i],++v[i],add(v[i],u[i]);
++m,u[m]=v[m]=2,w[m]=0,dfs(2);
for(int i=1;i<=m;++i)if(cn[u[i]]&&cn[v[i]]){
if(tv[u[i]]>w[i])clr(to[u[i]]),tv[u[i]]=w[i];
if(tv[u[i]]==w[i])to[u[i]].push_back(v[i]);
}
clr(ae[0]),ae[0].push_back(1),dl=(n<<1)+20;
for(int i=1,t=0;i<=dl;++i,t^=1){
mn=10,clr(ae[t^1]),++TIM;
for(int j=0;j<ae[t].size();++j){
p=ae[t][j];
if(tv[p]<mn)mn=tv[p],clr(ae[t^1]),++TIM;
if(tv[p]==mn)for(int k=0;k<to[p].size();++k)if(li[to[p][k]]!=TIM)li[to[p][k]]=TIM,ls[to[p][k]][i+1]=p,ae[t^1].push_back(to[p][k]);
}
ans[++nw]=mn;
}
stp=0;
for(int i=0;i<ae[0].size()&&!stp;++i){
tg=sz[0]=sz[1]=0;
for(int j=dl,id=ls[ae[0][i]][dl+1];j>=1&&!stp;id=ls[id][j],--j){
ar[tg][++sz[tg]]=id;
if(id==ae[0][i])(++tg)==2?stp=ae[0][i]:0;
}
if(stp){
if(sz[0]!=sz[1])stp=0;
else for(int k=1;k<=sz[0];++k)ar[0][k]!=ar[1][k]?stp=0:0;
}
if(stp)l1=nw-(sz[0]<<1);
}
for(int i=1;i<=l1;++i)prt=(10ll*prt+ans[i])%mod;
for(int i=l1+1;i<=nw;++i)v1=(10ll*v1+ans[i])%mod;
v2=POW(POW(10,mod-2),nw-l1),v1=1ll*v1*v2%mod*POW(1-v2+mod,mod-2)%mod;
printf("Case #%d: %lld\n",fr,1ll*POW(POW(10,mod-2),l1)*(prt+v1)%mod);
}
return 0;
}
其实并不是很难。
考虑设\(dp_{i,j}\)表示打完前\(i\)个字符,目前剪切板里的内容是\([i-j+1,i]\)(即这个端是由粘贴得到)的最小代价。\(j=0\)表示剪切板里没有内容(或者不关心剪切板里的内容,即\(dp_{i,0}\)对\(dp_{i,j}\)取\(\min\))。
那么可以预处理出\(lst_{i,j}\)表示子串\([i,j]\)最晚一次出现在和\([i,j]\)不交的位置是在哪里(左端点)。这个可以\(O(n^2)\)得出。
然后考虑如何计算\(dp_{i,j}\):
首先,\(dp_{i,0}=dp_{i-1,0}+X\)
如果\(lst_{i-j+1,i}\)存在(记为\(p\)),那么\(dp_{i,j}=min(dp_{j-1,0}+Y+Z,dp_{p+j-1,j}+(j-(p+j-1)-1)\times X+Z)\)
code:
#include<bits/stdc++.h>
using namespace std;
const long long INF=1e15;
int T,n,X,Y,Z,a[5010],*t,tmp,lst[5010],ls[5010][5010],lt[5010][5010],tg[5010],ind[5010],ad[5010][5010],TIM,lc[5010][5010],pos[5010],sz,nw;
long long dp[5010][5010];
map<int,int>ap;
int main(){
scanf("%d",&T);
for(int fr=1;fr<=T;++fr){
scanf("%d%d%d%d",&n,&X,&Y,&Z),ap.clear(),tmp=0;
for(int i=1;i<=n;++i)lst[i]=0;
for(int i=1;i<=n;++i)scanf("%d",&a[i]),t=&ap[a[i]],!(*t)?(*t)=++tmp:0,a[i]=(*t),ls[i][i]=lt[i][i]=(lst[a[i]]?lst[a[i]]:0),lst[a[i]]=i;
for(int len=2;len<=n;++len){
tmp=0,++TIM;
for(int i=1,j=i+len-1;j<=n;++i,++j){
if(ls[i][j-1]){
ind[i]=ind[ls[i][j-1]];
if(lc[ind[i]][a[j]]==TIM)ls[i][j]=ad[ind[i]][a[j]];
else ls[i][j]=0;
lc[ind[i]][a[j]]=TIM,ad[ind[i]][a[j]]=i;
}else ls[i][j]=0,ind[i]=++tmp,lc[tmp][a[j]]=TIM,ad[tmp][a[j]]=i;
}
for(int i=n-len+1;i>=1;--i)if(tg[i]!=TIM){
sz=0;
for(int t=i;t;t=ls[t][t+len-1])tg[t]=TIM,pos[++sz]=t;
nw=sz+1;
for(int t=sz;t>=1;--t){
while(pos[nw-1]+len-1<pos[t])--nw;
lt[pos[t]][pos[t]+len-1]=(nw<=sz?pos[nw]:0);
}
}
}
for(int i=1;i<=n;++i){
dp[i][0]=dp[i-1][0]+X;
for(int j=1;j<=i;++j){
dp[i][j]=INF;
if(lt[j][i])dp[i][j]=min(dp[j-1][0]+Y+Z,dp[lt[j][i]+(i-j)][lt[j][i]]+Z+1ll*X*(j-1-(lt[j][i]+(i-j))));
dp[i][0]=min(dp[i][0],dp[i][j]);
}
}
printf("Case #%d: %lld\n",fr,dp[n][0]);
}
return 0;
}
几何题我直接跑路。
首先,我们发现如果两个矩形的\(IoU>threshold\),那么两个的交应该大于某个值\(V\),这个值可以轻松计算得到\(V=\frac{2S^2T}{T+1}\)。
那么我们考虑两个正方形的交要大于\(V\),他们的四个角之中的某一个应该满足一些条件,我们以左下角为例,假设两个正方形的左下角分别为\((x_1,y_1)\)和\((x_2,y_2)\),且\(x_1\le x_2,y_1\le y_2\)。
那么应该满足\((x_1+S-x_2)\times(y_1+S-y_2)>V\)。由于这个值只与两点的相对关系有关,不妨假设\(x_1=y_1=0\)。
那么对\(x_2,y_2\)的限制变为
我们把限制画到平面直角坐标系上,即下图中红色区域:
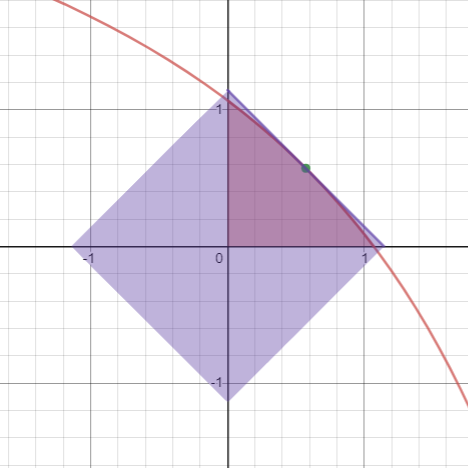
而且我们发现无论\(S,V\)取何值,红色区域都是相似的。
我们可以惊喜地发现,事实上满足条件,而且可以同时被加入的\((x_2,y_2)\)只有\(O(1)\)个。
但是这个区域事实上是一个类似反比例函数的一部分,因此不是很好统计。不过我们可以把它近似成一个菱形(图中蓝色区域)并统计。于是我们可以暴力找出菱形中的点并直接判断两者是否满足条件。
至于怎么找,正确的找法应该是按照菱形将坐标系分成块,然后给每个点定位到一个块(显然每个块里只有\(O(1)\)个点),然后满足条件的点只可能在这个点周围的块中(还是\(O(1)\)个)。
但是写完莫名其妙WA了,于是写了个假算通过了此题(
code(当然是假算):
#include<bits/stdc++.h>
#define ci const int&
#define pi pair<int,int>
#define f first
#define s second
using namespace std;
struct elem{
int x,y,id;
double rk;
}p[100010];
int T,n,S,lm,fl,ans,prt[100010],tx,ty;
long long V;
double tmp;
set<pi>s1,s2,s3,s4;
set<int>p1,p2,p3,p4;
set<pi>::iterator it;
set<int>::iterator ii;
bool tag;
bool cmp(elem x,elem y){
return x.rk>y.rk;
}
bool Check(ci x,ci y,ci cx,ci cy){
return 1ll*(S-abs(x-cx))*(S-abs(y-cy))>=V;
}
int main(){
scanf("%d",&T);
for(int fr=1;fr<=T;++fr){
scanf("%d%d%lf",&n,&S,&tmp),V=ceil(2.0*S*S*tmp/(tmp+1)+1e-9),lm=2*(S-sqrt(V*1.0));
if(fr==1&&n==92904)tag=1;
ans=0,p1.clear(),p2.clear(),p3.clear(),p4.clear(),s1.clear(),s2.clear(),s3.clear(),s4.clear();
for(int i=1;i<=n;++i)scanf("%d%d%lf",&p[i].x,&p[i].y,&p[i].rk),p[i].id=i;
sort(p+1,p+n+1,cmp);
for(int i=1;i<=n;++i){
fl=0;
for(ii=p1.lower_bound(p[i].x);!fl&&ii!=p1.end()&&(*ii)<=p[i].x+lm;++ii)for(it=s1.lower_bound((pi){*ii,p[i].y});!fl&&it!=s1.end()&&(*it).f==*ii;++it){
tx=*ii,ty=(*it).s;
if((tx-p[i].x)+(ty-p[i].y)>lm)break;
fl|=Check(p[i].x,p[i].y,tx,ty);
}
for(ii=p2.lower_bound(-p[i].x-S);!fl&&ii!=p2.end()&&(*ii)<=-p[i].x-S+lm;++ii)for(it=s2.lower_bound((pi){*ii,p[i].y});!fl&&it!=s2.end()&&(*it).f==*ii;++it){
tx=-*ii,ty=(*it).s;
if((p[i].x+S-tx)+(ty-p[i].y)>lm)break;
fl|=Check(p[i].x,p[i].y,tx-S,ty);
}
for(ii=p3.lower_bound(p[i].x);!fl&&ii!=p3.end()&&(*ii)<=p[i].x+lm;++ii)for(it=s3.lower_bound((pi){*ii,-p[i].y-S});!fl&&it!=s3.end()&&(*it).f==*ii;++it){
tx=*ii,ty=-(*it).s;
if((tx-p[i].x)+(p[i].y+S-ty)>lm)break;
fl|=Check(p[i].x,p[i].y,tx,ty-S);
}
for(ii=p4.lower_bound(-p[i].x-S);!fl&&ii!=p4.end()&&(*ii)<=-p[i].x-S+lm;++ii)for(it=s4.lower_bound((pi){*ii,-p[i].y-S});!fl&&it!=s4.end()&&(*it).f==*ii;++it){
tx=-*ii,ty=-(*it).s;
if((p[i].x+S-tx)+(p[i].y+S-ty)>lm)break;
fl|=Check(p[i].x,p[i].y,tx-S,ty-S);
}
if(fl)continue;
prt[++ans]=p[i].id;
p1.insert(p[i].x),p2.insert(-p[i].x-S),p3.insert(p[i].x),p4.insert(-p[i].x-S);
s1.insert((pi){p[i].x,p[i].y}),s2.insert((pi){-p[i].x-S,p[i].y}),s3.insert((pi){p[i].x,-p[i].y-S}),s4.insert((pi){-p[i].x-S,-p[i].y-S});
}
sort(prt+1,prt+ans+1);
printf("Case #%d: %d\n",fr,ans);
for(int i=1;i<=ans;++i)printf("%d%c",prt[i]," \n"[i==ans]);
}
return 0;
}
我直接不会
结论是如果\(1\)是某条直径的中点,那么后手胜,否则先手胜。
至于证明,大概就是如果\(1\)不是直径中点。那么先手每次将棋子从当前位置移动到直径上关于直径中点和当前点对称的点,那么后手每次都会移动到离直径中点更远的位置。而如果一开始棋子就在中点上,先手就只能把棋子移到不是直径中点的位置,然后后手可以仿照上述策略。
所以问题变为求一棵树上有多少连通块的直径是\(1\)。可以树形dp。似乎可以做到\(O(n)/O(n\log n)\)。
还没写,先鸽着。
首先去除串中原有的\(SAD\)。
如果没有单个的\(A\),那么每个\(SAD\)一定是将一个以\(-S\)为结尾的拼上以\(AD-\)为前缀的,或者\(-SA\)拼上\(D-\)。这个直接数即可。特判连成环的情况,这种情况下答案减一。
在考虑单个的\(A\),它一定会接在某个\(-S\)为结尾的上。因此枚举有几个\(S\)后面接了\(A\)即可。
还没写,先鸽着。
结论是\((i,j)\)这个块放在\((i,j,0)\)和\((i,j,1)\)的位置。然后你发现所有颜色为\(x\)的全部都连在了一起。
code:
#include<bits/stdc++.h>
using namespace std;
int T,n;
int main(){
scanf("%d",&T);
for(int fr=1;fr<=T;++fr){
scanf("%d",&n);
printf("Case #%d:\nYES\n",fr);
for(int i=1;i<=n;++i)for(int j=i;j<=n;++j)printf("%d %d %d %d 0 %d %d 1\n",i,j,i,j,i,j);
}
return 0;
}
太长了不敢看。
首先,段数相当于统计\(i\)存在而\(i+1\)不存在的对数。因此一个对\((i,i+1)\)会在从\(i\)到\(LCA(i,i+1)\)的路径上产生贡献。
用tarjan可以做到\(O(n)\),当然树剖之类的应该也能过,甚至\(O(n\log^2n)\)的dsu可能也能。
首先发现路径不会很多,最多也就长成这样:
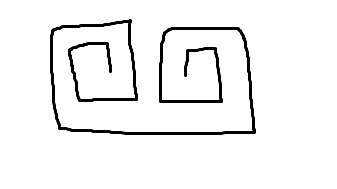
这样的东西应该只有\(2(n+m)\)个,打个表发现答案是\(2(n+m)-4\)。
当然要特判\(n,m\)中有\(1\)的情况。
code:
#include<bits/stdc++.h>
using namespace std;
int T,n,m;
int main(){
scanf("%d",&T);
for(int fr=1;fr<=T;++fr){
scanf("%d%d",&n,&m);
printf("Case #%d: ",fr);
if(n==1&&m==1)puts("1");
else if(n==1||m==1)puts("2");
else printf("%d\n",((n+m)<<1)-4);
}
return 0;
}
标签:break writer ref -o else and href 技术 pac
原文地址:https://www.cnblogs.com/xryjr233/p/CCPC_Final_2019.html