案例分析|主成分分析之一二三+案例

标签：相关   方法   思想   规模   biee   性问题   附件   降维   png   

⑴高等代数/线性代数：线性方程组、特征值和特征向量

⑵统计学：方差分析等

2.主成分分析思想：

主成分分析是利用降维的思想，在损失较少信息的前提下，用几个综合指标来代替之前多个指标的一种多元统计方法。我们把这些综合指标称为主成分，其中每一个主成分是原来变量的线性组合 ，并且各个主成分之间互不相关 。

3.主成分分析的几点要求

⑴每一个主成分都是原始变量的线性组合。

⑵主成分的数目要求远远小于原始变量的数目。

⑶主成分保留了原始变量绝大多数的信息。

⑷各个主成分之间互不相关。

4.主成分分析的理论框架

选取主成分的几点选择方法

⑴累积贡献率达到85%。

⑵观察碎石图，当趋势变的平稳，则说明选取该主成分的数量比较合适。

⑶选取特征值大于1的主成分。

主成分的几条重要的理论性质

⑴第 k个主成分 Y(k)与原始变量 的相关系数 称为因子负荷量，这个因子负荷量在软件操作中可以显示出来。如果我们用协方差矩阵来求解主成分，那么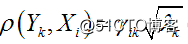 ，因此，我们在解释主成分和某个变量的重要性的时候，要根据因子负荷量而不是简单的变换系数 ；我们用相关矩阵来求解主成分，则 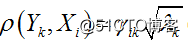(一般当变量的数据数量级差别比较大，我们要进行标准化处理，就会用到用相关矩阵来求解主成分)。

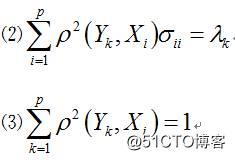
性质2和3在附件例子来讲述。

5.主成分的几个很重要的用途

⑴进行分类

我们可以通过主成分分析得到主成分得分，通过计算出总得分来进行分类，或者将前两个主成分得分放到四象限图中来进行分类。

⑵进行排名

通过主成分分析得到主成分得分，通过一定的手段计算出总得分来进行对样本的排名。

⑶ 主成分回归

由于在实际问题中，我们尽可能多的选取变量，这样会导致多重共线性问题的出现。主成分分析可以用少数几个综合变量来代替原始的变量，很有效的消除多重共线性。

↓↓↓ 点击"阅读原文" 可下载相关案例

天善智能 www.hellobi.com 是一个专注于商业智能BI、数据分析、数据挖掘和大数据技术的垂直社区平台。

问答社区和在线学院是国内最大的商业智能BI 和大数据领域的技术社区和在线学习平台，技术版块与在线课程已经覆盖 商业智能、数据分析、数据挖掘、大数据、数据仓库、Microsoft BI、Oracle BIEE、IBM Cognos、SAP BO、Kettle、Informatica、DataStage、Halo BI、QlikView、Tableau、Hadoop 等国外主流产品和技术。

线上活动：Friday BI Fly 每周五晚 20:30，技术和行业交流，20余个微信直播群互动交流。

线下活动：Saturday BI Fly 在全国各大城市巡回举办200人-500人规模的大数据沙龙交流活动，每月1-2次。

天善智能积极地推动国产商业智能 BI 和大数据产品与技术在国内的普及与发展。

案例分析|主成分分析之一二三+案例

标签：相关   方法   思想   规模   biee   性问题   附件   降维   png   

原文地址：https://blog.51cto.com/15009253/2552757