标签:bsp 产生 长度 mes cout 位置 span ack 这一
题意就是算子区间内的不同质因子的个数
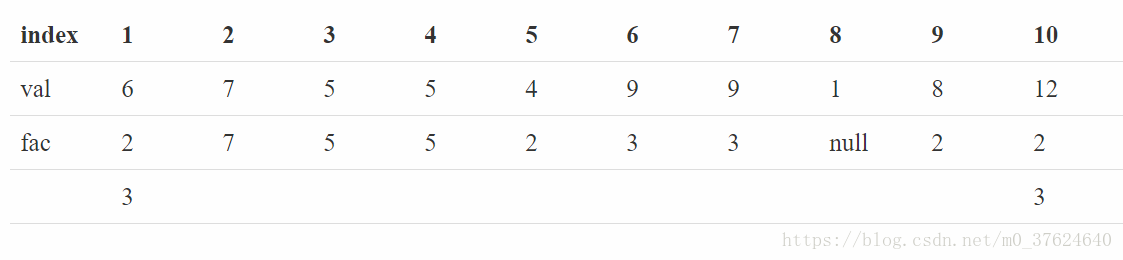
题目大意:有一个长度为n的序列a,定义mul(l, r)为区间[l, r]中a[i]的乘积,
fac(l, r)为mul(l, r)不同素数因子的个数。求所有区间fac的和。
和这个题有点类似
给定一个长度为n的序列,然后求出每一个子区间不同数的个数和。而这一道题就是组合计数,计算每一个位置上的值对最后区间计数所产生的贡献。
而这道题类似,略微修改即是每一个位置上不只一个值(分解可能得到多个质因子),所以就用vector来存放。
所以他的贡献就是

#include<iostream> #include<algorithm> #include<vector> using namespace std; typedef long long ll; const int maxn=1e6+100; vector<int>v[maxn]; int prime[maxn]; bool biaoji[maxn]; int a[maxn]; int cnt=0; void get(){ for(int i=2;i<maxn;i++){ if(!biaoji[i]) prime[++cnt]=i; for(int j=1;j<=cnt&&i*prime[j]<maxn;j++){ biaoji[i*prime[j]]=1; if(i%prime[j]==0){ break; } } } } void di(int x){ int t=a[x]; for(int j=1;j<=cnt&&prime[j]*prime[j]<=t;j++){ if(t%prime[j]==0){ v[prime[j]].push_back(x); while(t%prime[j]==0){ t/=prime[j]; } } } if(t!=1){ v[t].push_back(x); } } int main(){ get(); int n; cin>>n; for(int i=2;i<=maxn;i++){ v[i].push_back(0); } for(int i=1;i<=n;i++){ cin>>a[i]; di(i); } ll ans=0; for(int i=1;i<=cnt;i++){ for(int j=1;j<v[prime[i]].size();j++){ ans=ans+1ll*(v[prime[i]][j]-v[prime[i]][j-1])*1ll*(n-v[prime[i]][j]+1); } } cout<<ans<<endl; }
标签:bsp 产生 长度 mes cout 位置 span ack 这一
原文地址:https://www.cnblogs.com/lipu123/p/14019088.html