标签：mamicode   字典序   单词   需要   return   变量   数组   字典   初始   

第一题 5605. 检查两个字符串数组是否相等

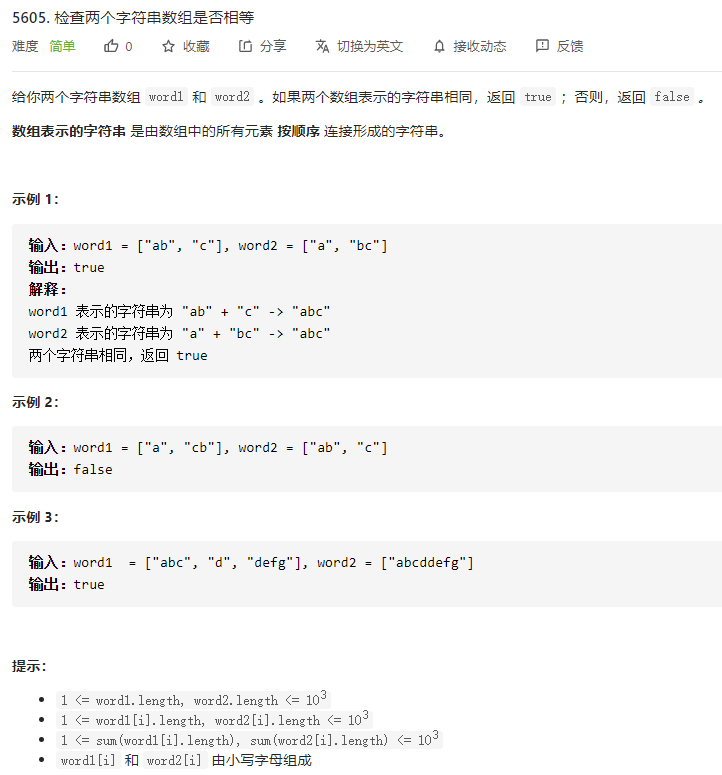
对于每个数组，都连接这个数组的所有单词为一个单词，然后直接判断这两个单词是否相等即可。

class Solution {
public:
    bool arrayStringsAreEqual(vector<string>& word1, vector<string>& word2) {
        string w1, w2;
        for(auto &word : word1) {
            w1 += word;
        }
        for(auto &word : word2) {
            w2 += word;
        }
        return w1 == w2;
    }
};

第二题 5606. 具有给定数值的最小字符串

贪心，从前往后填充n位的字符串，对于当前的每一位，都填充能够满足要求的、字典序最小的字符。

满足要求指：当前位填充了这个字母之后，后面未填充的字符串的数字之和能够达到要求（即n位单词的各位总和仍有可能为k）。

代码如下：

class Solution {
public:
    string getSmallestString(int n, int k) {
        string res = "";
        while(n > 0) {            // n表示当前还未填充的位数有n个
            int cur = 1;          // cur表示当前位上填的数的值，cur为1时表示当前位填‘a‘, cur为2时表示当前位为‘b‘...
            while(!((n - 1) <= k - cur && k - cur <= 26 * (n - 1)) && cur <= 26) {   // 填充了这一位后，未填充的位数就是 n - 1,只有 k - cur大于等于 n - 1且k - cur小于等于26 * (n - 1)时，剩下的位的数值的和才可能满足要求
                ++cur;                 // 如果这一位的字母的数值是cur会导致后面的数值和无法满足要求，那么就让cur加一
            }
            res += ‘a‘ + cur - 1;     // 这一位填数字cur对应的字母（满足要求的情况下，字典序最小的填法）
            --n;                      // 后面需要填充的位数减一
            k -= cur;                 // 后面的数值和为 k - cur
        }
        return res;
    }
};

第三题 5607. 生成平衡数组的方案数

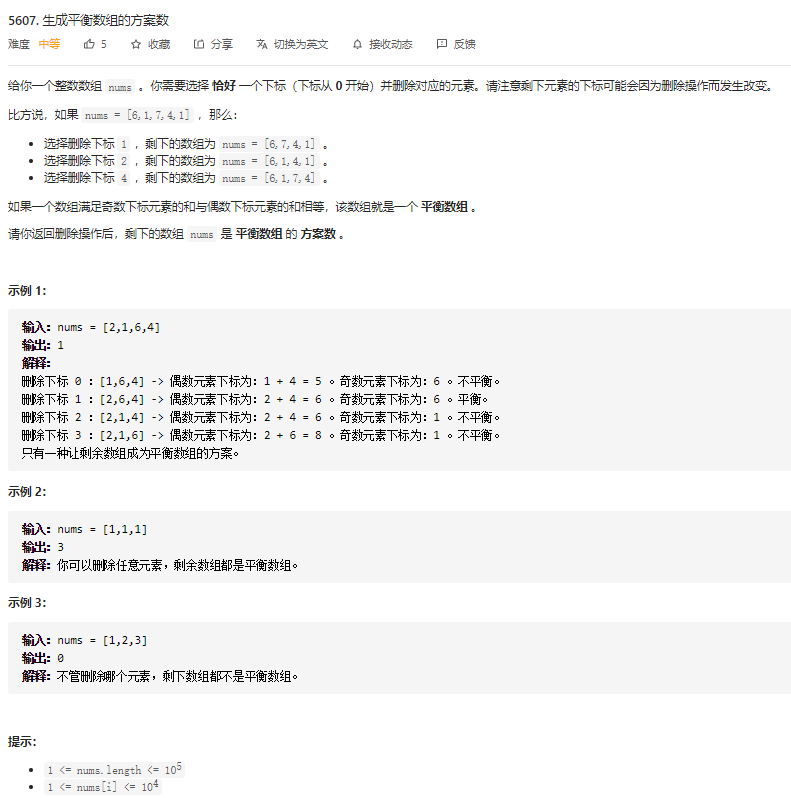
题目需要求奇数下标的和和偶数下标的和，很容易想到可以用两个前缀和数组preOddSum和preEvenSum来维护所有奇数下标的数的前缀和和偶数下标的数的前缀和。

由题意知，删去某一位后，它后面的数的下标原来是偶数的变成了奇数，原来是奇数的变成是偶数。所以删去某一位i之后奇数下标的数的和就是preOddSum[i - 1] + preEvenSum[n] - preEvenSum[i]，即i - 1的奇数下标的前缀和，和原数组中i + 1 ~ n的偶数下标的数的和（删去第i个数之后原来的偶数下标就变成了奇数下标），删去某一位i之后偶数下标的数的和同理:preEvenSum[i - 1] + preOddSum[n] - preOddSum[i]。

我们只需要预处理出两个前缀和数组之后，直接遍历数组，判断删去当前下标的数之后奇数下标元素的和是否与偶数下标元素的和相等即可。

代码如下：

class Solution {
public:
    int waysToMakeFair(vector<int>& nums) {
        int n = nums.size();
        vector<int> preOddSum(n + 1, 0);
        vector<int> preEvenSum(n + 1, 0);
        for(int i = 1; i <= n; ++i) {
            if(i % 2 == 0) {        // 在原数组中算奇数 
                preOddSum[i] = preOddSum[i - 1] + nums[i - 1];
                preEvenSum[i] = preEvenSum[i - 1];
            } else {
                preOddSum[i] = preOddSum[i - 1];
                preEvenSum[i] = preEvenSum[i - 1] + nums[i - 1];
            }
        }
        int res = 0;
        for(int i = 1; i <= n; ++i) {
            if(preOddSum[i - 1] + preEvenSum[n] - preEvenSum[i] == preEvenSum[i - 1] + preOddSum[n] - preOddSum[i]) {
                ++res;
            }
        }
        return res;
    }
};

第四题 5608. 完成所有任务的最少初始能量

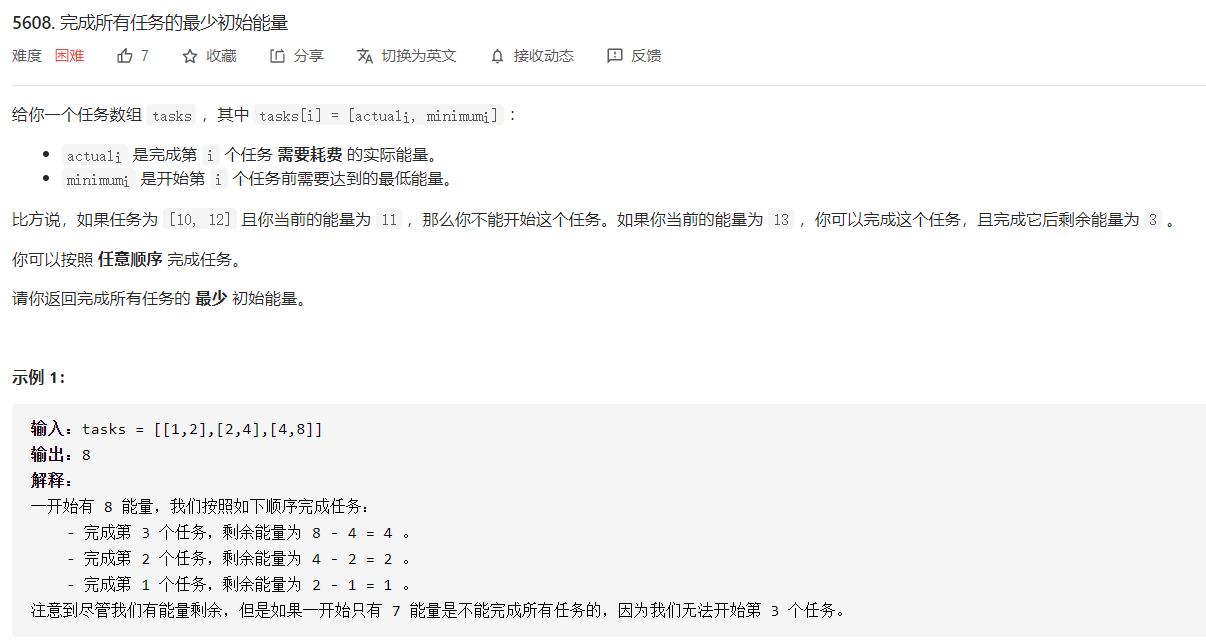
贪心，先处理最低能量minimum和消耗能量actual差值较大的task，即根据minumum - actual的差值对tasks数组从大大小拍个序，然后遍历tasks数组来处理任务。

用一个变量res记录最终答案，即需要的最小能量。再用一个变量curEnergy，表示处理当前任务需要的最低能量。

遍历每一个任务，如果curEnergy < tasks[i][1],表示当前能量没有达到开始第i个任务需要的最低能量，我们让res += tasks[i][1] - curEnergy，也就是通过提高初始能量的方式，使得开始第i个任务时，能量达到最低要求。

然后让curEnergy -= tasks[i][0]，表示处理掉了第i个任务，当前能量消耗掉了tasks[i][0]。

遍历完数组之后，res就是能够处理完所有任务的最低初始能量。

代码如下：

class Solution {
public:
    int minimumEffort(vector<vector<int>>& tasks) {   
        sort(tasks.begin(), tasks.end(), [&](const vector<int>& a, const vector<int>& b) {
           return a[1] - a[0] > b[1] - b[0]; 
        });
        int res = 0, curEnergy = 0;
        for(auto &v : tasks) {
            if(curEnergy < v[1]) {
                res += (v[1] - curEnergy);
                curEnergy = v[1];
            }
            curEnergy -= v[0];
        }     
        return res;
    }
};

LeetCode第216场周赛

标签：mamicode   字典序   单词   需要   return   变量   数组   字典   初始   

原文地址：https://www.cnblogs.com/linrj/p/14020296.html