标签:batch 接受 min mamicode 求导 等等 精选 角度 假设
主要内容(下划线部分):1、计算复杂性与NP问题
2、上溢和下溢
3、导数,偏导数及两个特殊矩阵
4、函数导数为零的二三事
5、方向导数和梯度
6、梯度有什么用
7、梯度下降法
8、牛顿法
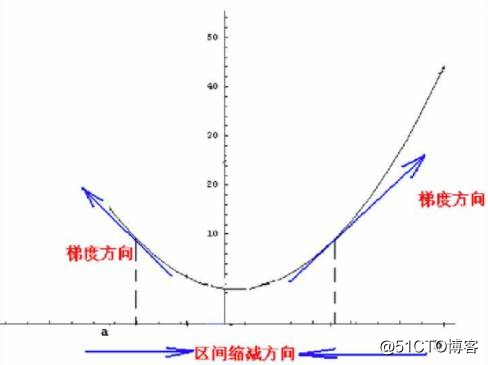
方向导数:在之前讲偏导数的时候,相信很多人已经看出,偏导数求的都是沿着坐标轴的变化率,不管多少维也好,都只是求的变化率,那现在问题来了,如果我想求在某个方向而不是沿着坐标轴方向的变化率怎么求呢?那方向导数,简单来说,就是我们指定任意一个方向,函数对对这个任意方向的变化率.
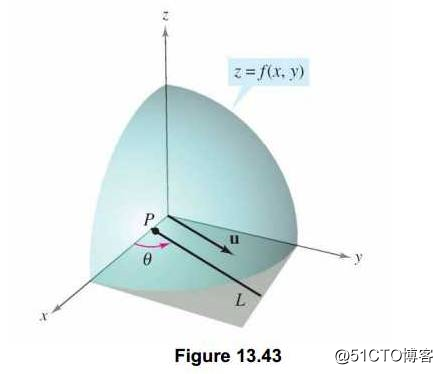

或者说,如下图,我们知道在一维的时候,函数的导数就是在某点对应切线的斜率,那么对于函数f(x,y)的 点在这个方向上也是有切线的,其切线的斜率就是方向导数。当然,注意这个切线是任意的,这里我们要限定其方向,也就是图中中的矢量y的方向。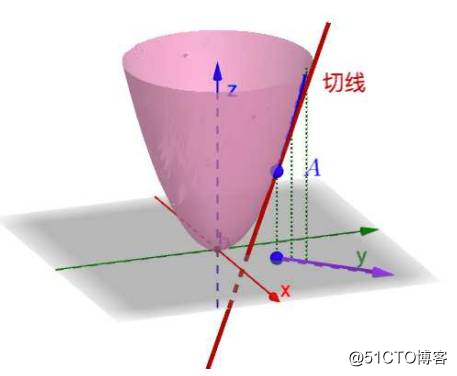
梯度:是一个矢量或者说是一个向量,其方向上的方向导数最大,其大小正好是此最大方向导数。
梯度的理解很重要,很重要,很重要!下面解决两个问题,梯度怎么求和梯度有什么用?
怎么算?--(介绍一种比较简单之间的方法)
方向导数可以如下的方法算:
简单的讲,假如你在一座山上,蒙着眼睛,但是你必须到达山谷中最低点的湖泊,你该怎么办?然后我们想到一个简单的方法,在每走一步时,都是走那个离谷底最近的那个方向,那怎么求才能使得每一步都下降更大的高度,这个时候我们就完全可以用梯度来帮助我们,就可以完成任务啦!
当然了,我们是在写机器学习数学基础呐,你会说下山有什么用,我们看这篇文章又不是为了下山的。Emmm...别急,下面我们就讲梯度的大用处
不知道讲清楚没有,这两个概念非常重要,下面的优化算法的前提就是梯度,要重点理解

注意:这里只是假设,不用知道这个目标函数就是平方损失函数等等,然后肯定有人问既然要最小化它,那求个导数,然后使得导数等于0求出不就好了吗?Emmmm...是的,有这样的解法,可以去了解正规方程组求解。
说下这里不讲的原因,主要是那样的方式太难求解,然后在高维的时候,可能不可解,但机器学习或深度学习中,很多都是超高维的,所以也一般不用那种方法。总之,梯度下降是另一种优化的不错方式,比直接求导好很多。
梯度下降:我们知道曲面上方向导数的最大值的方向就代表了梯度的方向,因此我们在做梯度下降的时候,应该是沿着梯度的反方向进行权重的更新,可以有效的找到全局的最优解。这个theta的更新过程可以描述为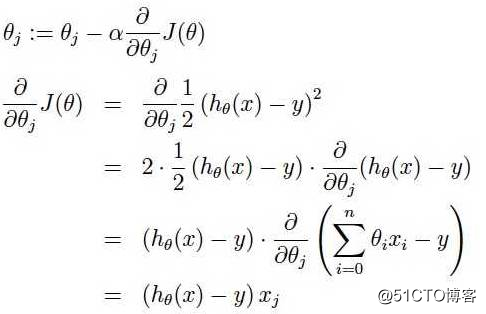
[a表示的是步长或者说是学习率(learning rate)]
好了,怎么理解?在直观上,还是下山,我们可以这样理解,看下图,一开始的时候我们随机站在一个点,把他看成一座山,每一步,我们都以下降最多的路线来下山,那么,在这个过程中我们到达山底(最优点)是最快的,而上面的a,它决定了我们“向下山走”时每一步的大小,过小的话收敛太慢,过大的话可能错过最小值,扯到蛋...)。
这是一种很自然的算法,每一步总是寻找使J下降最“陡”的方向(就像找最快下山的路一样)。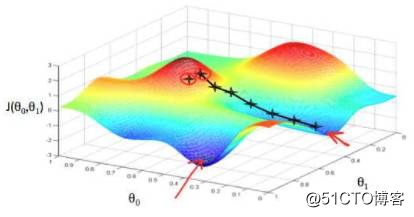
当然了,我们直观上理解了之后,接下来肯定是从数学的角度,我们可以这样想,先想在低维的时候,比如二维,我们要找到最小值,其实可以是这样的方法,具体化到1元函数中时,梯度方向首先是沿着曲线的切线的,然后取切线向上增长的方向为梯度方向,2元或者多元函数中,梯度向量为函数值f对每个变量的导数,该向量的方向就是梯度的方向,当然向量的大小也就是梯度的大小。现在假设我们要求函数的最值,采用梯度下降法,结合如图所示:

如果样本不多的情况下,当然是这样收敛的速度会更快啦。但是很多时候,样本很多,更新一次要很久,这样的方法就不合适啦。下图是其更新公式
随机梯度下降:在每次更新时用1个样本,可以看到多了随机两个字,随机也就是说我们用样本中的一个例子来近似我所有的样本,来调整θ,因而随机梯度下降是会带来一定的问题,因为计算得到的并不是准确的一个梯度,容易陷入到局部最优解中,但是相比于批量梯度,这样的方法更快,更快收敛,虽然是局部最优,但很多时候是我们可以接受的,所以这个方法用的也比上面的多。下图是其更新公式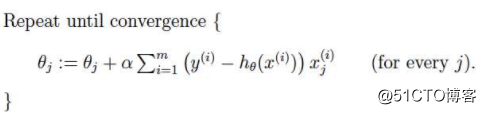

梯度下降算法是机器学习或者深度学习中经典算法,现在绝大部分算法都是这个,就算是改进,也是在此基础上做出的改进,所以,要知道这个算法是什么,了解它的思想,甚至推荐直接看论文。
先来讲怎么找一个函数的零点(也就是函数值为0的点),我们提出如下公式。

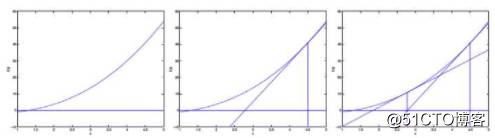

牛顿法:从之前讲的知道极值点就是导数为0的地方,但直接求导数等于0得到最优解在很多时候是不可行的,那我们现在试一下用就用上面的方式来求得极值点,也就是求导数的零点,也上面的方法应用到求导数为0时的点来求最值的方法就叫做牛顿法,对应的,牛顿方法的迭代规则如下:
其中H是一个n阶方阵(如果算上截距项应该是n+1阶方阵)的Hessian矩阵(两个特殊矩阵)。
相较于批量梯度下降,牛顿方法通常来说有更快的收敛速度,只需要少得多的迭代次数就能得到很接近最小值的结果。但是当模型的参数很多时(参数个数为n)Hessian矩阵的计算成本将会很大,导致收敛速度变慢,所以在深度学习中也很少使用牛顿法,就是因为计算Hessian矩阵太麻烦了,但是当参数个数不多时,牛顿方法通常又是比梯度下降快得多的。这也是他的优势吧
伪牛顿法:上述的牛顿法需要计算Hessian矩阵的逆矩阵,运算复杂度太高。在动辄百亿、千亿量级特征的大数据时代,模型训练耗时太久。因此,很多牛顿算法的变形出现了,这类变形统称拟牛顿算法。拟牛顿算法的核心思想用一个近似矩阵B替代逆Hessian矩阵H?1。不同算法的矩阵B的计算有差异,但大多算法都是采用迭代更新的思想在tranning的没一轮更新矩阵B。
由于这些伪牛顿法比较复杂,而且在机器学习中也较少用,所以在这里先不细讲了,有兴趣的小伙伴可以看下篇博文
牛顿法在基础机器学习中有用到,但在深度学习中很少用,我们知道是什么,基本了解就好
熬夜写完一,可能有些错别字,见谅!接下来就是二了,二比较烧脑了,写的也比较多,坚持!写的有什么不好,有任何建议可以大胆提出,感谢!
精选干货|近半年干货目录汇总
干货|掌握机器学习数学基础之优化[1](重点知识)
【直观详解】什么是PCA、SVD
欢迎关注公众号学习交流~ 
标签:batch 接受 min mamicode 求导 等等 精选 角度 假设
原文地址:https://blog.51cto.com/15009309/2553982