标签:分割 问题 ble 复杂 理解 add img 出现 sep

前 言
这是 SVM 系列的第二篇,上一篇文章 【机器学习理论】我所理解的 SVM(支持向量机)- 1 介绍了 SVM 的主要思想以及推导过程,这一篇将会在此基础上介绍核函数(kernel),这也是 SVM 最为重要的部分之一。
文章地址:https://zhuanlan.zhihu.com/p/24291579恩是的,我终于回来更新了,让我们进入正题。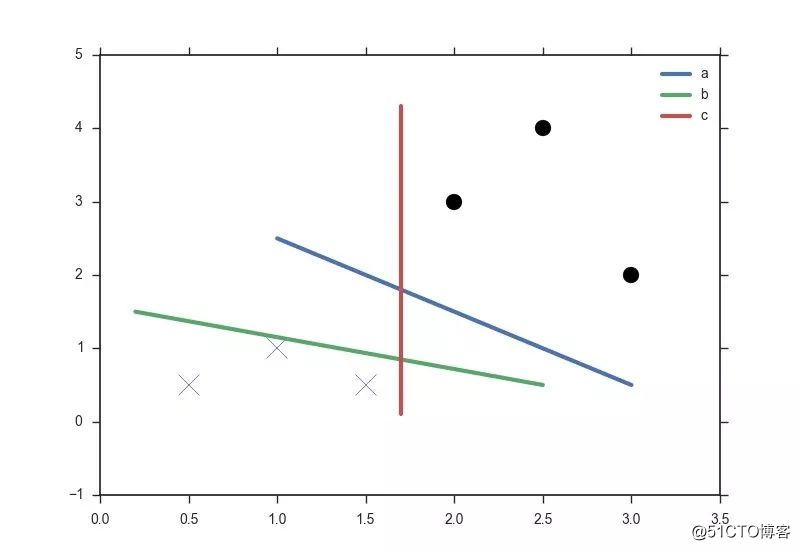
上面这幅图是不是很眼熟,在 SVM-1 中我几乎靠着这一张图说完了支持向量机的主要思想。
不知道你们注意到没有,在推导 SVM 之前,我的措辞是相当严谨的——「图中的两组数据,显然它们是线性可分(linear separable)的」,一切的推导都建立在线性可区分的基础上,然而实际的很多问题都并非如此,如果我在上面的图上再加一个点: 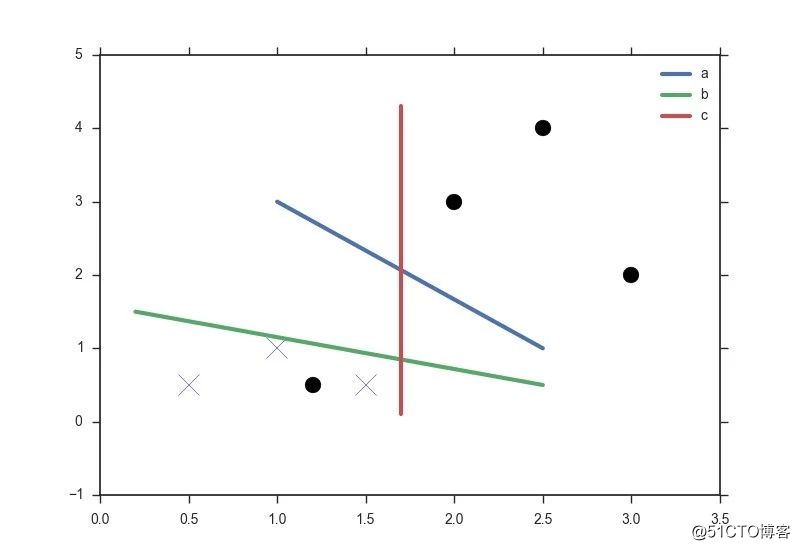
无论是a,b,c都无法完美地把两种数据区分出来,实际上也不存在一条直线能完全区分出两种数据,这种情况就是不可线性区分的,核函数或许可以帮我们解决这个问题。
上一篇文章的最后我们通过乘数法得到了 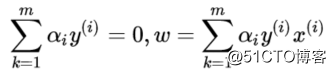
现在我们把它们回带到分界线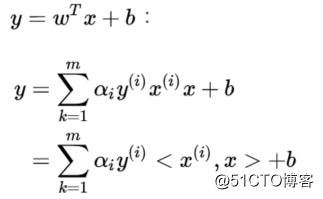

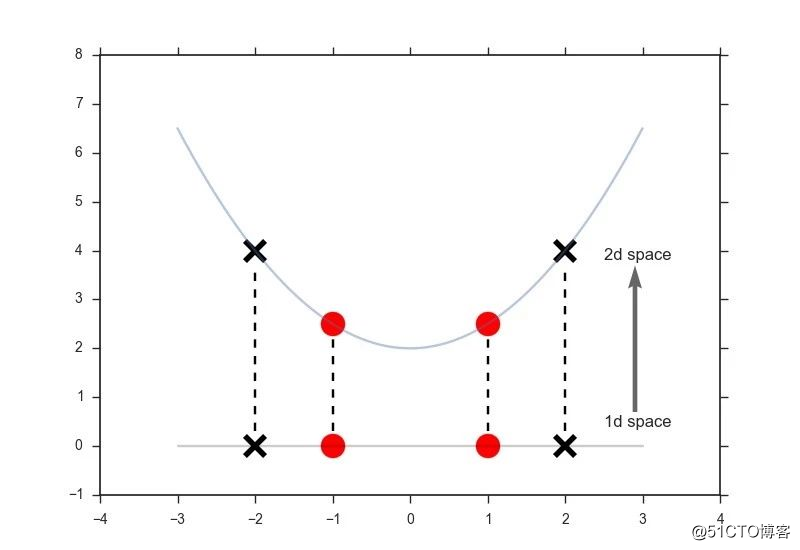


通过映射函数,我们能从原始数据中(低维空间)抽象出所需的特征(高维空间),由低维空间向高维空间的转化很多时候非常的麻烦。
有意思的是,无论是1维、10维、100维还是更高维的空间,其矢量点积的结果都是一个常数,那么有没有什么捷径,可以跳过维度转换的过程,通过相对简单的计算直接得到矢量积?答案就是核函数,还是举一个例子来说明吧:
$$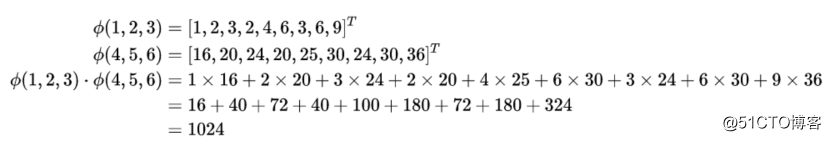
可以看出计算相当繁琐,嗯,我们来尝试找找对应的核函数: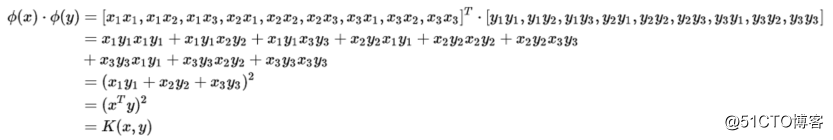
通过上面的推导,我们发现虽然维度转化的过程较为繁琐复杂,但是矢量点积的结果确实相当简洁,这一次我们直接用核函数计算: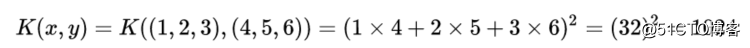
相比于从低维映射到高维空间再进行矢量积运算,核函数大大简化了计算的过程,使得向更高维转化变为了可能,我们不需要知道低维空间的数据是怎样映射到高维空间的,我们只需要知道结果是怎么计算出来的。
在支持向量机中常用的几种核函数是多项式型核(Polynomial Kernel)、径向基函数核(Radial basis function kernel,又叫高斯核,简称 RBF)以及逻辑核( Sigmoid Kernel)。

维数越高,偏差(bias)越低,方差(variance)越高,容易出现过拟合的情况,相反维数越低,偏差就会越大,但是方差会随之减小,一般不宜选择过高的维度,最适合的维度需要通过交叉验证(cross validation)等方法来确定。
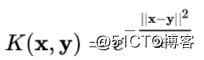
也可以写成这样的形式: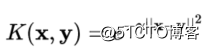

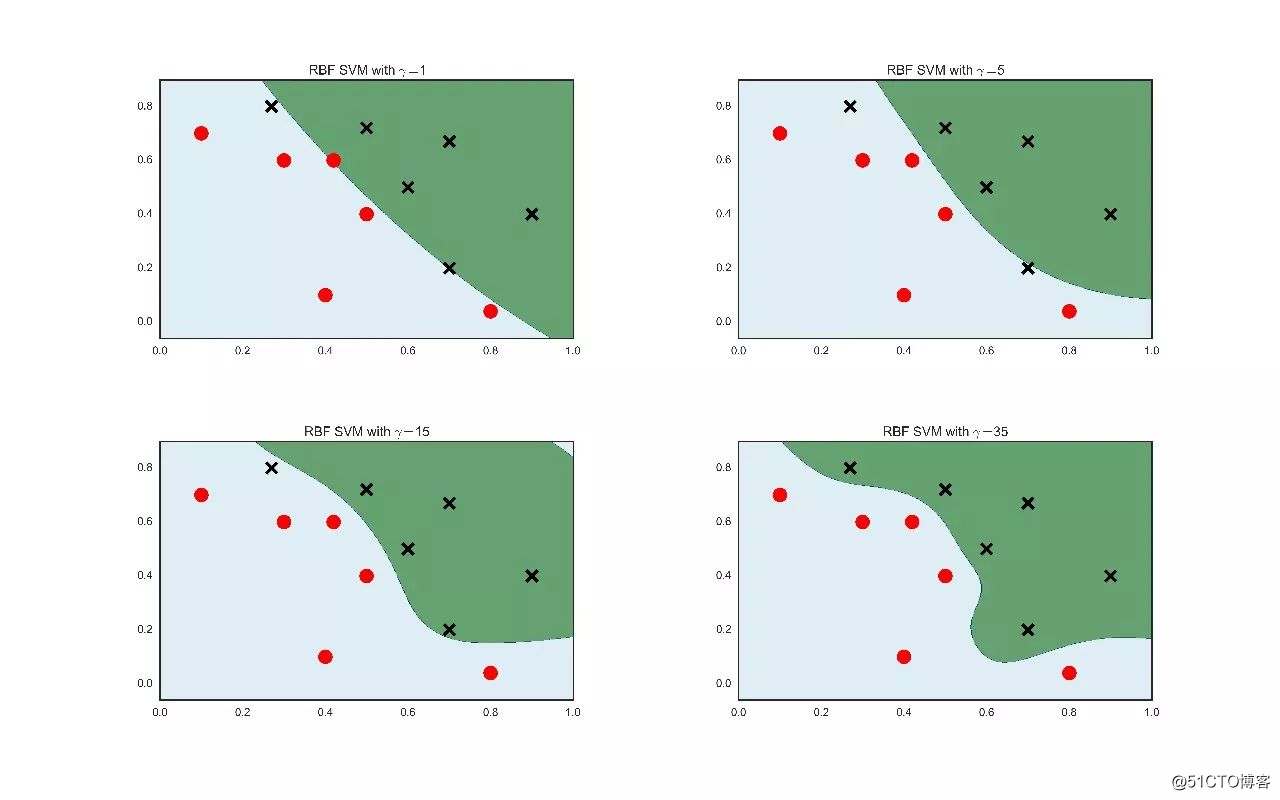

选择合适的核函数并不是一件容易的事情,因为评估数据点之间的相似度往往需要专业领域的知识,幸运的是大多数情况下高斯核都能取得不错的结果。
核函数并不是支持向量机专用的技巧,任何算法只要能写成向量相乘的形式就可以运用核函数进行优化。
一个正确的核函数对于数据相似度有着正确的描述,两个矢量越接近重合,相似度越大,越接近正交相似度越小,多项式型核和高斯核都是正确的核函数,那么对于核函数正确与否的一般标准是什么呢?让我们引入核矩阵。
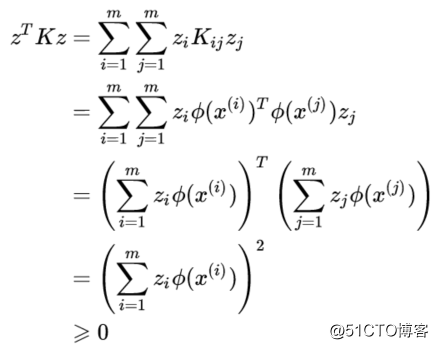
我们证明了核函数的一个必要条件是对应的核矩阵为半正定对称矩阵,事实上这个条件是充分且必要的,也就是 Mercer‘s theorem:
原本想在这篇文章里写完 SVM 的核函数和正则化的,但是第一篇和第二篇之间间隔太长,很多东西都得重新看一遍,写核函数部分花了太长时间,还有一些东西尚未提及,比如正则项、不完美分割,当初是计划在SVM 的第三篇介绍 SMO 算法的,现在看来得重新规划一下了。
【深度学习实战】pytorch中如何处理RNN输入变长序列padding
【基础数学知识】带你理解泰勒展开式本质?
【基础算法】最易懂的 Alpha-Beta 剪枝算法详解
欢迎关注公众号学习交流~ 
标签:分割 问题 ble 复杂 理解 add img 出现 sep
原文地址:https://blog.51cto.com/15009309/2554199