格林公式及其推论的推导与应用

标签：曲线   连通   play   导数   load   splay   简单   范围   loading   

格林某式： 设闭区域 \(D\) 由分段光滑的曲线 \(L\) 所围成，函数 \(P(x,y)\)及\(Q(x,y)\)在 \(D\) 上具有一阶连续 偏导数，则有\(\iint \limits_D (\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy=\oint_L Pdx+Qdy\)其中 \(L\) 是 \(D\) 的取正向的边界曲线.

证明

有人讲推没推导一下格林公式反映学习态度，乐乐表示实名害怕。为了证明我是真的有认真在学习，就勉为其难简单推一下算了。

二重积分和曲线积分的相似之处就是最终总会转化为定积分求解，不如把式子里四个积分都拿出来转化成定积分。
\(\iint \limits_D \frac{\partial Q}{\partial x}dxdy\) ???? \(\iint \limits_D \frac{\partial P}{\partial y}dxdy\)

\(\oint_L P(x,y)dx\)????\(\oint_L Q(x,y)dy\)

就这四个

假设区域 \(D\) 是X&Y型，可转定积分如下：

1. 当Y型：
   
2. 当X型：
   

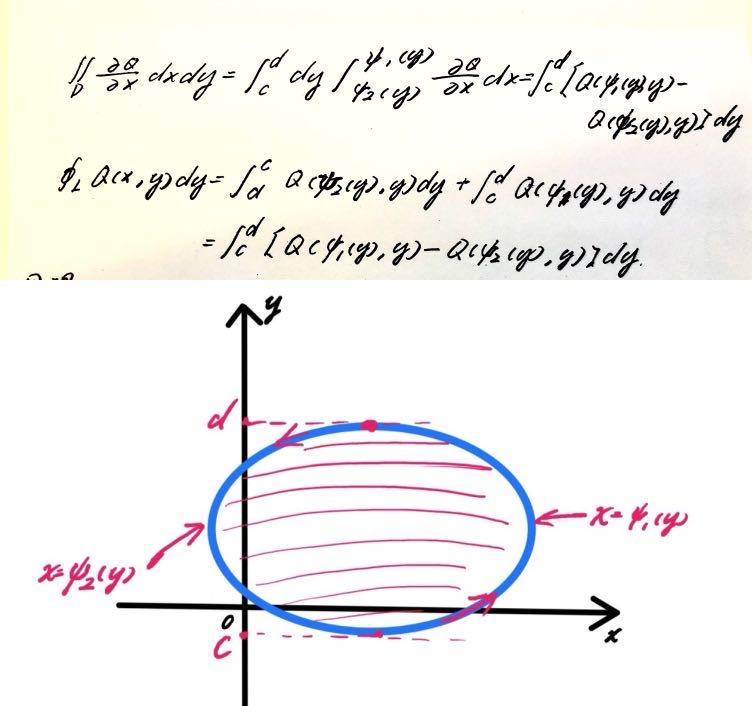
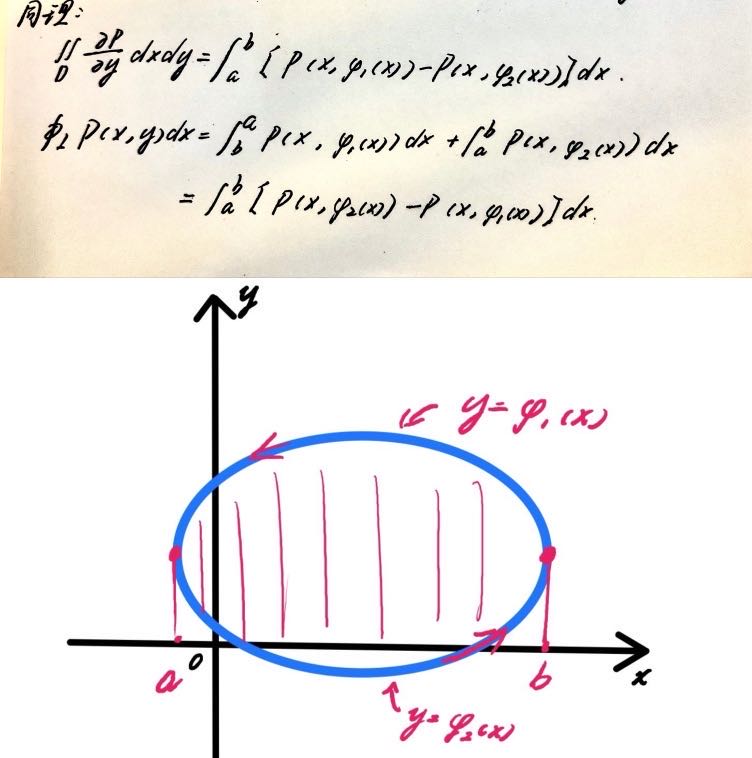
于是发现\(\iint \limits_D \frac{\partial Q}{\partial x}dxdy=\oint_L Q(x,y)dy\)

一经叠加就有：

故在X&Y型区域上格林公式得证。

对于任意非X&Y型区域或者多连通区域，总能划分成若干X&Y型单连通区域。

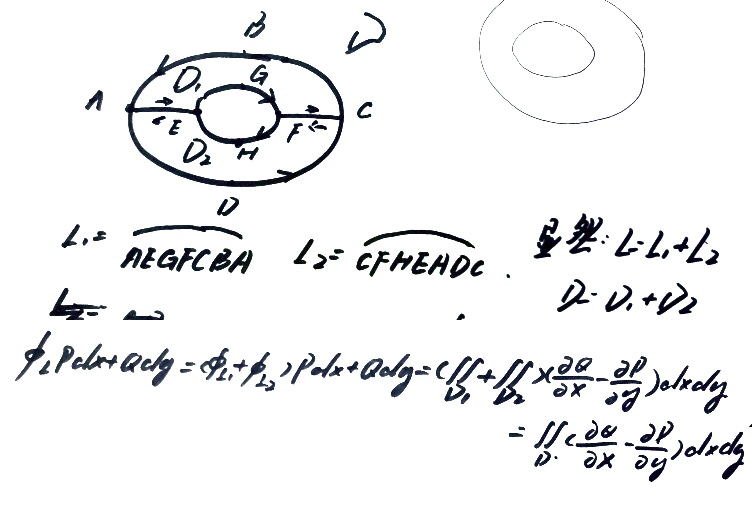
故只要闭区域由任意分段光滑的曲线围成，且函数 \(P(x,y)\)及\(Q(x,y)\)在 该区域上 上有一阶连续偏导数，\(\iint \limits_D (\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy=\oint_L Pdx+Qdy\)就成立，格林公式就得证了。

推论

面积公式曲线积分形式

\(A=\iint\limits_D dxdy=\frac{1}{2}\iint\limits_D \frac{\partial (x)}{\partial x}-\frac{\partial (-y)}{\partial y}dxdy=\oint_L xdy-ydx\)
（为直角坐标形式，参数形式也直接往里代，积分上下界就是 \(t\) 的范围）

曲线积分与路径无关的条件

当区域内\(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}=0\) 或者说 \(\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}\)时，

任意两个起点终点分别相同而路径不同的曲线\(L_1\),\(L_2\)，\(L_1\)与\(L_{2^-}\)总能构成闭合曲线 \(L\)

则

即与路径无关.

待续

格林公式及其推论的推导与应用

标签：曲线   连通   play   导数   load   splay   简单   范围   loading   

原文地址：https://www.cnblogs.com/zouludaxia/p/14052989.html