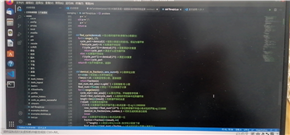
def problem(area=10): # 随机生成一道题目(自然数四则运算或分数运算),运算符不超过3个
try:
if random.choice([1, 2]) == 1: # 随机生成 自然数或分数 的四则运算
expression, print_expression = natural(area) # 生成一个自然数运算
# 运算结果通过demical_to_fraction()转成分数
results = demical_to_fraction(eval(expression))
else: # 分数四则运算 和上面流程大致相同
expression, print_expression = fraction(area) # 生成一个分数运算
results = demical_to_fraction(eval(expression))
if not results: # 无法转分数
problem(area)
return 0
# print_expression_nums = list(filter(str.isdigit, print_expression)) # [‘2‘,‘+‘,1‘]
print_expression_nums = print_expression.replace(
‘(‘, ‘‘).replace(‘)‘, ‘‘).split() # 将输出表达式拆解
print_expression_nums.sort() # [‘+‘, 1‘, ‘2‘]
if results < 0 or ((str(results) in answers) and (print_expression_nums in str_num)): # 去负答案,去重复
problem(area)
else:
results = turn_fracrtion(results) # 转化
prints.append(print_expression)
answers.append(results) # 答案列表
str_num.append(print_expression_nums)
except Exception: # 过滤分母为0的题目
problem(area)
def natural(area): # 生成一个自然数运算
operator_num = random.randint(1, 3) # 随机运算符
expression = print_expression = num = str(random.randint(1, area)) # 第一个数
bracket = (random.choice(
[‘(‘, ‘‘]) if not operator_num == 1 else ‘‘) # 非单运算符 可加括号
for i in range(operator_num): # 随机个运算符
op = str(random.choice(operators)) # 随机选择运算符 (+ - * /)
if op == ‘-‘: # 若为‘-‘,生成数字小于前一个数字
num = str(random.randint(1, int(num)))
else:
num = str(random.randint(1, area)) # 随机数值,不超过area
if bracket == ‘)‘: # 右括号在数字右边
print_expression += ‘ ‘ + \
change(op) + ‘ ‘ + num + bracket # 用于输出的表达式 例:1×2
expression += op + num + bracket # 用于eval()计算的表达式 例:1*2
else: # 左括号在数字左边
print_expression += ‘ ‘ + change(op) + ‘ ‘ + bracket + num
expression += op + bracket + num
bracket = (‘)‘ if bracket == ‘(‘ else ‘‘) # 左括号配右括号, 空配空
return expression, print_expression
def gen_fraciton(area): # 生成一个规范分数
while True:
a = random.randint(1, area)
b = random.randint(1, area)
if ‘/‘ in str(Fraction(a, b)):
return Fraction(a, b)
def fraction(area): # 生成一个分数运算
operator_num = random.randint(1, 3) # 随机运算符
num = gen_fraciton(area)
expression = print_expression = str(num) # 第一个分数
bracket = (random.choice(
[‘(‘, ‘‘]) if operator_num != 1 else ‘‘) # 超过一个运算符才需要加括号
for i in range(operator_num):
op = str(random.choice(operators))
if op == ‘-‘: # 若为‘-‘,生成分数小于等于前一个分数
while True:
next_num = gen_fraciton(area)
if next_num <= num:
break
num = next_num
else:
num = gen_fraciton(area)
if bracket == ‘)‘:
if float(num) > 1: # 假分数转带分数 例:8/3 -> 2‘2/3
print_expression += ‘ ‘ + \
change(op) + ‘ ‘ + turn_fracrtion(num) + bracket
else:
print_expression += ‘ ‘ + change(op) + ‘ ‘ + str(num) + bracket
expression += op + str(num) + bracket
else:
if float(num) >= 1:
print_expression += ‘ ‘ + \
change(op) + ‘ ‘ + bracket + turn_fracrtion(num)
else:
print_expression += ‘ ‘ + change(op) + ‘ ‘ + bracket + str(num)
expression += op + bracket + str(num)
bracket = (‘)‘ if bracket == ‘(‘ else ‘‘) # 左括号配右括号
return expression, print_expression
def turn_fracrtion(results): # 假分数转带分数
if isinstance(eval(str(results)), int) or (eval(str(results)) < 1): # 整数和真分数
return str(results)
else:
return str(int(results)) + "‘" + str(results - int(results)) # 假分数
def change(a): # *,/ 转成 ×,÷
if a == ‘*‘:
a = ‘ב
elif a == ‘/‘:
a = ‘÷‘
return a
def find_cycle(demical): # 找小数的循环体(参数为小数部分)
for i in range(1, 17):
cycle_part = demical[:i] # 截取小数部分的前i位,假设为循环体
if len(cycle_part) < 4: # 如果循环体较短
if (cycle_part*3) == demical[:3*i]: # 需要满足4次重复
return cycle_part # 满足才认定为循环体
else: # 如果循环体较长
if (cycle_part*2) == demical[:2*i]: # 满足2次重复
return cycle_part
return 0 # 找不到循环体,返回0
def demical_to_fraction(n, zero_num=0): # 小数转化分数
n = str(n) # 规范输入为字符串形式
if len(n) < 16: # 如果是有限小数,直接返回
return Fraction(n)
real_num, dot_area = n.split(‘.‘) # 获取整数 和 小数
float_num = float(n) # 转化一个浮点数用于计算
for i in range(len(n)):
cycle_start = dot_area[i:] # 从第i位开始,开始截取字符串
result = find_cycle(cycle_start) # 从截取的字符串中找到循环体
length = len(str(result)) # 判断循环体的长度
if result: # 如果存在循环体
if i != 0: # 如果循环体的开始不是小数点后第一位 eg 0.13888888
new_number = float_num*(10**i) # 移位数使循环体是小数点后的开始 eg 13.8888
demical_to_fraction(new_number, i) # 将新生成的数递归使用
break
else: # 如果循环体直接在小数点后的第一位
fraction = Fraction(int(result), int(
‘9‘*length)) # 小数部分转化为分数 /数学知识需要了解
final_num = int(real_num) + fraction # 小数点前的部分需要从重新加上
return final_num/(10**zero_num) # 回退移的位数