P1679 神奇的四次方数

标签：注意   ble   stream   opened   其它   open   递推   load   i++   

P1679 神奇的四次方数

取还是不取,取的话取多少,完全背包.

注意初始化的问题.

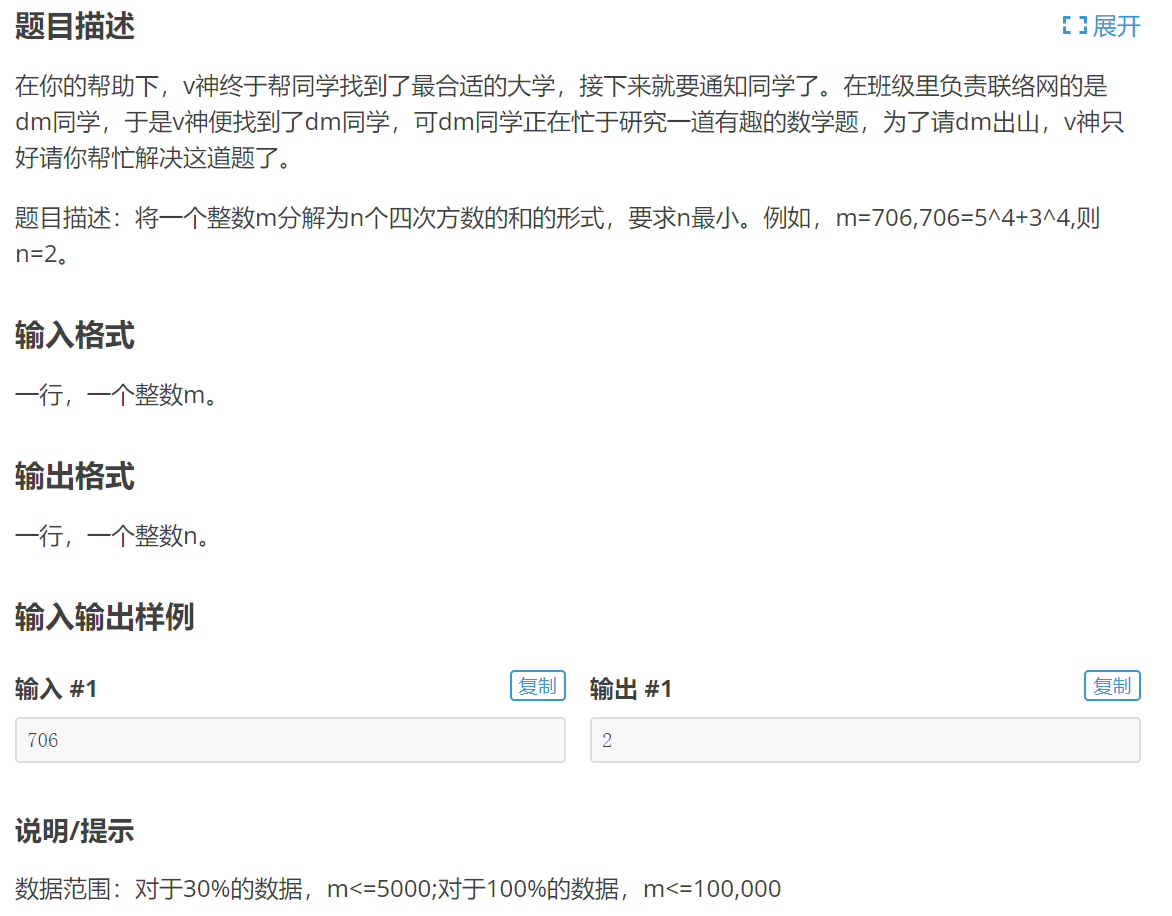
 完全背包问题,dp[i][j]表示前i个数(第i个数即为i⁴)中j的最小分解位数.比如(压维后)dp[1] = 1, dp[2] = 2(即1⁴ + 1⁴),dp[17] = 2(即2⁴ + 1⁴), dp[706] = 2(即3⁴ + 5⁴).

有dp[i + 1][j] = min(dp[i][j], dp[i][j - s[i]] + 1),s[i]为i⁴.

压维.

显然,如果不对dp进行初始化,最终dp仍然全部为0,如何解决呢?一种想法是:

if(dp[j])

　　if(dp[j - s[i]]) dp[]=...
　　else dp[]=...

else if(dp[j - s[i]]) dp[]=...

else dp[]=...

事实上,只需要:

for(int i = 1; i <= m; i++) dp[i] = 100000000;　　　　// 注意 dp[0] 仍然为0

可知所有的无效位最后均会在取min时被忽略,而初始的唯一有效位dp[0]最终会递推出其它所有有效位.例如i = 1循环结束后:

(此处dp大小为1000仅因为方便调试)

 所有位均变为有效位.(dp[i] = i)

为什么把dp[0]初始化为0恰好可以产生正确的结果呢?类似的问题最近刷题已经很常见到了.

就这题分析,显然地,当某一时刻dp所有位均为有效值时,之后所有时刻的值均为有效值并可求出答案.

那么只需要使得这一时刻尽早到来,观察这题的循环:

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;

int s[20], m, n, dp[100010];

int main() {
    cin >> m;
    for (int i = 1; i <= 18; i++) s[i] = i * i * i * i;

    for(int i = 1; i <= m; i++) dp[i] = 100000000;　　// INF
    // dp[1] = 1;
    for (int i = 1; i <= 18; i++)
        for(int j = s[i]; j <= m; j++)
            dp[j] = min(dp[j], dp[j - s[i]] + 1);

    cout << dp[m] << endl;

    return 0;
}

i = 1,j 从s[i](即1)直到m,首先可知dp[1] = min(INF, dp[0] + 1),此后,dp[j + 1] = min(INF, dp[j] + 1).

i = 1这一轮循环后不再存在INF,即dp所有位均为有效值.

想出构造的方法导向这个状态即可,不需要过分考虑内在的逻辑性(本题 "0" 似乎不能由 0 个数的四次方表示).

再结合本题,可以猜测涉及到取min时可以初始化dp为INF来处理无效位.类似地,涉及到取max时可以考虑初始化dp为0来应对.

你不觉得AC代码已经贴在上面了吗?

View Code

P1679 神奇的四次方数

标签：注意   ble   stream   opened   其它   open   递推   load   i++   

原文地址：https://www.cnblogs.com/Gaomez/p/14104990.html