标签:code 注意 ssis rev 思想 个数 row ace 编号
ST表的功能很简单
它是解决RMQ问题(区间最值问题)的一种强有力的工具
它可以做到O(nlogn)预处理,O(1)查询最值
ST表是利用的是倍增的思想
拿最大值来说
我们用Max[i][j]表示,从i位置开始的2j个数中的最大值,例如Max[i][1]表示的是i位置和i+1位置中两个数的最大值
那么转移的时候我们可以把当前区间拆成两个区间并分别取最大值(注意这里的编号是从1开始的)
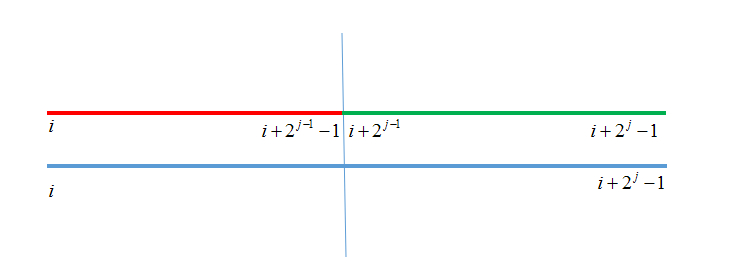
查询的时候也比较简单
我们计算出log2(区间长度)
然后对于左端点和右端点分别进行查询,这样可以保证一定可以覆盖查询的区间
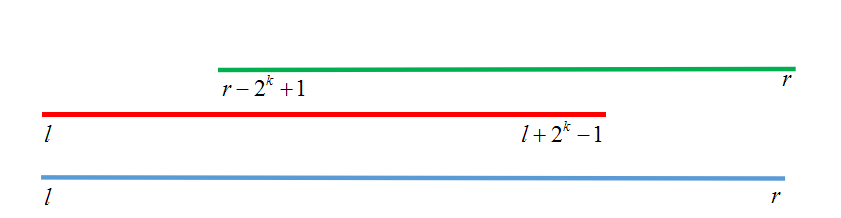
刚开始学的时候我不太理解为什么从右端点开始查的时候左端点是r?2k+1
实际很简单,因为我们需要找到一个点x,使得x+2k?1=r
这样的话就可以得到x=r?2k+1
上面讲的可能比较抽象,建议大家画个图好好理解一下
代码:
#include <bits/stdc++.h> using namespace std; const int MAXN=1e6+10; int Max[MAXN][21]; int Query(int l,int r) { int k=log2(r-l+1); return max(Max[l][k],Max[r-(1<<k)+1][k]);//把拆出来的区间分别取最值 } void st(int N) { for(int i=1;i<=N;i++) cin>>Max[i][0]; for(int j=1;j<=21;j++) //也可写成(1 << j) <= N for(int i=1;i+(1<<j)-1<=N;i++)//注意这里要控制边界 也可写成(1 << j) <= N Max[i][j]=max(Max[i][j-1],Max[i+(1<<(j-1))][j-1]);//如果看不懂边界的话建议好好看看图 } int main() { int N,M; cin>>N>>M; st(N); for(int i=1;i<=M;i++) { int l,r; cin>>l>>r; printf("%d\n",Query(l,r)); } return 0; }
标签:code 注意 ssis rev 思想 个数 row ace 编号
原文地址:https://www.cnblogs.com/shmilky/p/14105785.html