标签:表格 pen 开始 规划 经典 src png exce inpu
微信公众号:Jerry的算法和NLP
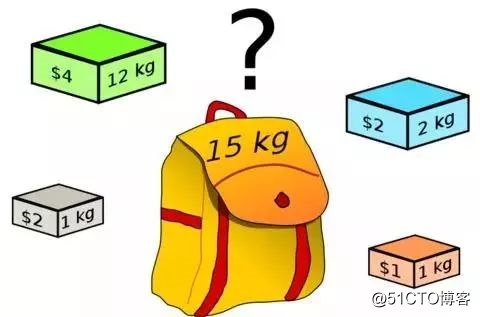
背包问题是一个经典的动态规划模型。它既简单形象容易理解,又在某种程度上能够揭示动态规划的本质,故不少教材都把它作为动态规划部分的第一道例题.

4 6
1 2 3
2 4 1
3 4 3
4 5 210与零一背包不同的是,零一背包中的物品是不可以重复拿取的,只可以拿取当前物品或者不拿取当前物品,不可以拿取多个,完全背包的物品是可以任意拿取多个的来构成不超过背包容量并且构成的总价值是最大的.
而这道题是多重背包问题,也就是这个物品的个数是有限个的,在物品个数范围内可以任意选择
动态规划的核心是找到dp公式或者状态转移的方程,理解清楚中间的过程是怎么样进行变化的,因为动态规划总是要利用到之前上一个物品选择后的最佳方案,所以dp数组里面存储的肯定是历史上存储的最佳方案,一开始的时候我们是可以借助excel表格来帮助我们理解dp数组是怎样生成的
建立一个二维数组f[i][j],定义为i为遍历到第i个物品的时候,j为背包的容量大小,j最大为m,如f[2][3]指的就是遍历到第二个物品下容量为3的最大价值
首先先遍历物品,再遍历容量。
由于每个物品的个数都不一样,所以我们还要遍历一下物品个数,看看物品是否都能放入背包中。
假设现在第一个物品的输入是1 2 3 代表着 体积为1 ,价值为2, 物品数量为3。
那么首先我们的嵌套第一层循环为物品 ,第二层循环为体积 ,第三层循环为物品数量 ,看看当前如果是这么多的物品能不能同时放入背包中 。
伪代码为
1for i 遍历物品
2 for j 遍历体积 从小到大
3 for k 遍历当前物品个数
4 当k*体积<=背包容量的时候 说明我们的背包是可以放下这么多物品的
5 dp[i][j]=max ( dp[i-1][j-k*wi]+k*vi , dp[i-1[j])
6 这个表达式的意思就是 要么选择K个这样的物品,要么不选,看看哪个是最优的解,然后更新即可
7
8 当k*体积<背包容量的时候说明我们的背包是放不下这么多物品的
9 直接就是dp[i][j]=dp[i-1][j]更新第一轮之后表格变化为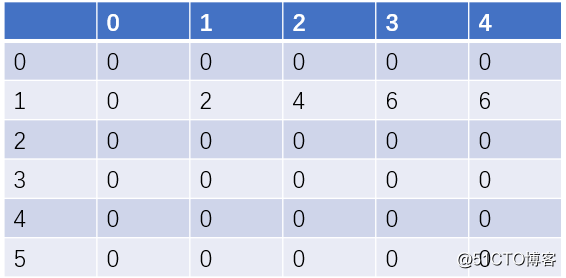
第二个物品更新完后是这样的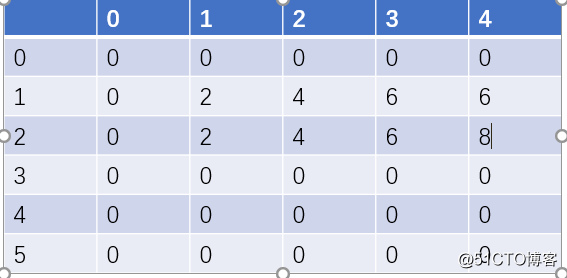
到最后直接输出dp[-1][-1]即可 代表着遍历到最后一个物品 最大容量下的最优解
1a=input()
2N,V=list(map(int,a.split()))
3w=[0]
4v=[0]
5s=[0]
6for i in range(N):
7 b=input()
8 wi,vi,si=list(map(int,b.split()))
9 w.append(wi)
10 v.append(vi)
11 s.append(si)
12
13dp=[[0 for i in range(V+1)]for i in range(N+1)]
14for i in range(V,-1,-1):
15 for j in range(s[1],0,-1):
16 if i>=j*w[1]:
17 dp[1][i]=max(dp[1][i-j*w[1]]+j*v[1],dp[1][i])
18
19for i in range(2,N+1):
20 for j in range(V+1):
21 for k in range(s[i]+1):
22 if j>=k*w[i]:
23 dp[i][j]=max(dp[i-1][j-w[i]*k]+v[i]*k,dp[i][j])
24 else:
25 dp[i][j]=max(dp[i-1][j],dp[i][j])
26print(dp[-1][-1])2020大厂笔试 | 网易提前批(1)
2020大厂笔试 | 网易提前批(2)
令人头疼的背包九讲(1)0/1背包
令人头疼的背包九讲(2)完全背包
腾讯笔试的几道题

标签:表格 pen 开始 规划 经典 src png exce inpu
原文地址:https://blog.51cto.com/15054042/2564180