标签:动态 了解 经典 二进制优化 image 输入 背包问题 问题 pen
微信公众号:Jerry的算法和NLP
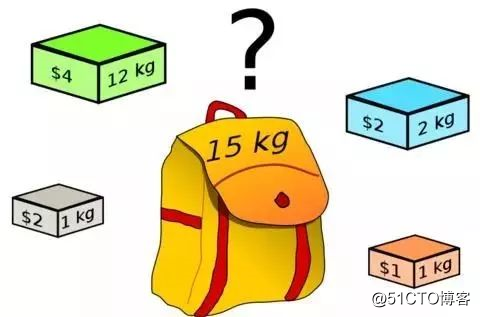
背包问题是一个经典的动态规划模型。它既简单形象容易理解,又在某种程度上能够揭示动态规划的本质,故不少教材都把它作为动态规划部分的第一道例题.

4 5
1 2 3
2 4 1
3 4 3
4 5 210与零一背包不同的是,零一背包中的物品是不可以重复拿取的,只可以拿取当前物品或者不拿取当前物品,不可以拿取多个.
完全背包的物品是可以任意拿取多个的来构成不超过背包容量并且构成的总价值是最大的.
多重背包问题,也就是这个物品的个数是有限个的,在物品个数范围内可以任意选择
如果对其中任意一个不了解,请看之前的推送
令人头疼的背包九讲(1)0/1背包
令人头疼的背包九讲(2)完全背包
令人头疼的背包九讲(3)多重背包
而这道多重背包问题我们可以看到,它的数据量是10^3,也就是说三次for循环后,整个的时间复杂度会达到10^9,超过了一秒中机器运行的10^8.
所以我们要对这个物品的个数进行优化。

首先我们的物品个数是用十进制的方式进行表达的,那么我们可以首先将十进制的物品转换为若干个二进制的物品。
具体怎么转换?我来举个例子你就懂了。
假设物品A是有10个,那么我将它进行拆分成1+2+4+3个
如果我要选择3个A,那么我的选择就是1+2
如果我要选择5个A,那么我的选择就是2+3
好像很amazing 这样的话物品的个数就可以由若干个转换成二进制的物品表示了(当时我还真的是从1-10都试了一遍)
那么我们来看看复杂度 复杂度方面的话原来应该是10^9
现在我们把这个转换成0/1背包问题,要么选这个,要么不选,原来是10次循环,现在变成了4次,原来的数据量是1000,现在变成了log(1000)+1
1a=input()
2N,V=list(map(int,a.split()))
3w=[0]
4v=[0]
5s=[0]
6for i in range(N):
7 b=input()
8 wi,vi,si=list(map(int,b.split()))
9 k=1
10#先把十进制转换成若干个二进制的物品
11
12 while si-k>0:
13 w.append(wi*k)
14 v.append(vi*k)
15 s.append(k)
16 si=si-k
17 k=k*2
18 if si>0:
19 w.append(wi*si)
20 v.append(vi*si)
21 s.append(si)
22dp=[[0 for i in range(V+1)]for j in range(len(w))]
23#开始循环 但是这个时候复杂度变成了10^6,不再是10^9,这道题主要就是考察这个
24for i in range(1,len(w)):
25 for j in range(1,V+1):
26 if j>=w[i]:
27 dp[i][j]=max(dp[i-1][j-w[i]]+v[i],dp[i-1][j],dp[i][j])
28 else:
29 dp[i][j]=max(dp[i-1][j],dp[i][j])
30print(max(dp[-1]))剑指offer刷题交流群
扫码添加微信,一定要备注研究方向+地点+学校+昵称(如机器学习+上海+上交+汤姆),只有备注正确才可以加群噢。

▲长按加群

标签:动态 了解 经典 二进制优化 image 输入 背包问题 问题 pen
原文地址:https://blog.51cto.com/15054042/2564178