Leetcode （213）| 打家劫舍 2

时间：2020-12-21 11:13:08 阅读：0 评论：0 收藏：0 [点我收藏+]

微信公众号：Jerry的算法和NLP

| 题目

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

| examlple:

示例 1:

1输入: [2,3,2]
2输出: 3
3解释: 你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

示例 2:

1输入: [1,2,3,1]
2输出: 4
3解释: 你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
4     偷窃到的最高金额 = 1 + 3 = 4 。

| 分析：

这应该是动态规划的一道比较中等的题目了，上一次讲到的题目是他的弟弟：
Leetcode （198）| 打家劫舍
考虑所有可能的抢劫方案过于困难，而且复杂度一定会超时

抓住题目中的条件，

相邻两个房屋不能同时偷窃
房屋之间形成了一个环

这意味着要抢第一个屋，最后一个屋就不能抢
抢最后一个屋，第一个屋就不能抢
而且抢了这个第N个屋子，N+1和N-1的屋子也不能抢

技术图片

首先考虑下Base case
n=0 return 0
n=1 return nums[0]
n=2 假设为a,b要么抢a 要么抢b return max(nums)
n=3 假设为a,b,c 要么抢a,要么b,要么c return max(nums)

n=4 假设为a,b,c,d
如果我一开始打算抢a,那么d我是够不着了，所以我只能从a,b,c里进行递归
如果我一开始不打算抢b,那么d是在我考虑的范围内，我从b,c,d里进行挑选

对于 n >=4，有两个选项:
抢第1个房子，去掉最后一个房子。
不抢第1个房子，保留最后一个房子。
显然，你想选择数额更大的选项。于是，可以总结出公式：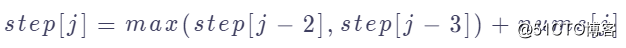
技术图片

所以你只需要考虑两种情况，然后就两种情况的最大值取最大即可。

代码：

python

 1class Solution:
 2    def rob(self, nums: List[int]) -> int:
 3        if not nums:
 4            return 0
 5        if len(nums)<=3:
 6            return max(nums)
 7        if len(nums)==4:
 8            return max(nums[0]+nums[2],nums[1]+nums[3])
 9        step=[0 for i in range(len(nums))]
10        step[0],step[1],step[2]=nums[0],nums[1],nums[0]+nums[2]
11        for i in range(3,len(nums)-1):
12            step[i]=max(step[i-2],step[i-3])+nums[i]
13        temp=max(step)
14        step=[0 for i in range(len(nums))]
15        step[1],step[2],step[3]=nums[1],nums[2],nums[1]+nums[3]
16        for j in range(4,len(nums)):
17            step[j]=max(step[j-2],step[j-3])+nums[j]
18        temp2=max(step)
19        return max(temp,temp2)

C++

 1int rob(vector<int>& nums)
 2{
 3    if (nums.size() == 1) return nums[0];
 4
 5    int sumOdd[2] = {0, 0}; // 0 == head, 1 == tail
 6    int sumEven[2] = { 0, 0 };
 7    for (int i = 0; i < nums.size(); i++)
 8    {
 9        for (int j = 0; j < 2; j++)
10        {
11            if (i == 0 && j == 1) continue; // head only
12            if (i == nums.size() - 1 && j == 0) continue;   // tail only
13            if (i % 2 == 0)
14            {
15                sumOdd[j] = max(sumOdd[j], sumEven[j]);
16                sumEven[j] += nums[i];
17            }
18            else
19            {
20                sumEven[j] = max(sumOdd[j], sumEven[j]);
21                sumOdd[j] += nums[i];
22            }
23        }
24    }
25
26    for (int j = 0; j < 2; j++)
27    {
28        sumOdd[j] = max(sumOdd[j], sumEven[j]);
29    }
30    return max(sumOdd[0], sumOdd[1]);
31}