令人头疼的背包九讲（1）0/1背包问题

时间：2020-12-21 11:13:59 阅读：0 评论：0 收藏：0 [点我收藏+]

标签：依次学校数字最大值序列长按堆排表达式输入格式

重磅干货，第一时间送达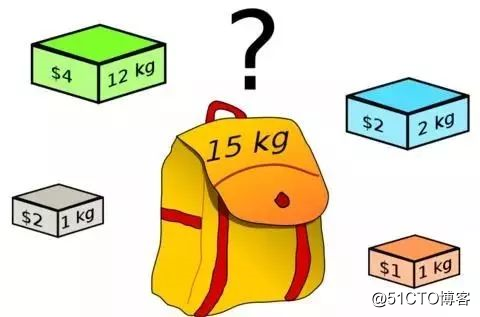
技术图片

背包问题是一个经典的动态规划模型。它既简单形象容易理解，又在某种程度上能够揭示动态规划的本质，故不少教材都把它作为动态规划部分的第一道例题.

题目

0/1背包问题

题目要求

有N件物品和一个容量为V的背包。第i件物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

输入格式

第一行两个整数，N,M空格隔开，分别表示物品数量和背包容积。

接下来有N行,每行两个整数vi,wi,空格隔开,分别表示第i件物品的体积和价格

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,M<1000
0<vi,wi<1000

输入样例

输出样例：

分析

0/1背包问题是最基本的背包问题，每个物品最多只能放一次或者选择不放。

思路A：一共有n个东西，背包容量为m，对于每个物品我们有两种选择方案，一个物品有两种，两个物品有四种，三个物品有八种，那么n个物品就有2^n种方案。穷举这2^n种方案，当n=100的时候，等于多少？
2的一百次方等于：1.26*10^30
这个数值是非常大的，例如存在一张可以充分折叠的纸厚度为0.1毫米，对半折一次，则厚度是0.2mm，再对折一次，是0.4mm……由此类推，对折n次，那么纸的厚度是：(2^n)×0.1mm
这个厚度的增长将呈指数增长的趋势，那么折了100次后，那么其长度到“134亿光年”，而宇宙大爆炸至今的全部时间仅仅才137亿年。
扯远了，就是为了说明这个穷举法不可取。
技术图片

思路B：动态规划的思想本质就是找到递归的表达式。在找递归的表达式的时候肯定是存在一定的边界限制（如青蛙跳台阶这种题目就没有限制）
那么这道题它给出了一个边界限制：容量M，当容量满的时候就再也放不下东西了，故我们在进行递归的时候需要考虑当前的容量，这就是我们的限制条件

目标函数是什么？目标函数就是我们的价值最大化max(value)

这个递归函数要怎么写？

这道题我打算用一维数组的做法来做，我先初始化一个数组叫f，长度为m+1(为了索引从1-m代表着容量从1-m),最后取f的最后一个元素即为答案。那么这个递归函数就可以表示为

f(m)=max(f(m),f(m-w[i])+v[i])
f(m) 当前背包容量为m的情况下不选择当前物品
f(m-w[i])+v[i] 当前背包容量为m情况下选择当前物品
m-w[i]代表着我这个背包在上一次选择中必须至少给我留下w[i]的空间，我才可以选择当前物品，然后得到它的价值v[i]

解题步骤

首先初始化f，将重量放到一个数组W(weighted)中，将价值放到一个数组V(value)中
其次开始遍历我的物品，一共n个，遍历我每一个物品的时候我都会使得我的背包容量依次递增（从1到m）。这一步什么意思？我们来举个例子
容量从1开始一直递增，假设第一个物品的weight=1,value=2,那么容量为1的时候f[1]=2，容量为2的时候f[2]=4 f[3]=6 ...??? 好像走错片场了。我们这个问题的前提是每个物品只能选择一次或者不选择使得利益最大化，那如果这个背包容量容量从1开始一直递增，我们这个问题就变成了每个物品可以选择多次。
为什么会变成这种情况，因为背包容量如果从少到多，它每次贪心max()的时候都会想，我还能不能放入更多的这个物品，现在放入一件了，能不能再放多一件。
怎么修改？把容量从m到1一直递减就可以了。f[m]=2,f[m-1]=2...f[1]=2
这种情况，因为背包容量如果从多到少，它每次贪心max()的时候，都是先看能不能放下一件当前物品,不会产生放置两件物品以上的情况。
最后我们把f输出，取最后一个元素即可

注意：分歧其实就在f[m-w[i]]，

如果容量从小到大遍历，那么到最后的f[m]取决的结果不是基于上一物品选择,而是取决于当前物品的选择

如果容量从大到小遍历，那么到最后的f[m]取决的结果是基于上一物品选择

代码

Python :

 1# 01背包问题 利用一维数组进行
 2a=input()
 3n,m=list(map(int,a.split()))
 4w=[0 for i in range(n+1)]
 5v=[0 for i in range(n+1)]
 6for i in range(1,n+1):
 7    b=input()
 8    w[i],v[i]=list(map(int,b.split()))
 9
10# 定义一个数组 f[j] 表示容量为j的情况下能放的总价值最大
11
12f=[0 for i in range(m+1)]
13print(f)
14for i in range(1,n+1):
15    for j in range(m,0,-1):#容量从大到小遍历
16        if j >=w[i]:
17            f[j]=max(f[j],f[j-w[i]]+v[i])
18        else:
19            break
20# j为容量不断上升 当容量大于当前的时候才可以放下这个
21print(f[-1])

C++

 1#include<bits/stdc++.h>
 2using namespace std;
 3const int N=1010;
 4
 5int f[N];
 6int v[N],w[N];
 7int n,m;
 8int main(){
 9    cin>>n>>m;
10
11    for(int i=0;i<n;i++){
12        cin>>v[i]>>w[i];
13    }
14
15    for(int i=0;i<n;i++){
16        for(int j=m;j>=v[i];j--){
17            f[j]=max(f[j],f[j-v[i]]+w[i]);
18        }
19    }
20    cout<<f[m]<<endl;
21}