标签:alt 接下来 -o 理论 learn 遇到 owa 自己 结构

看看这个美丽的森林,现在,假设你有机会在其中进行数据分析。你的任务是找出森林中每个区域的熊猫数量与树木数量的比。成功分析后,会发现树木的密度高于熊猫密度。转换为矩阵形式,差不多是这个样子:

图源:freepik.com
其中散落着一些可爱的大熊猫,但是矩阵的密度主要源于树木。设树木值=“0”,则熊猫值=任何非零值,表示为“1”。然后,该图像将变成由0和1组成的矩阵,这意味着整个矩阵的密度包括大量0和极少量1。
这种包括大量0和极少非0数值的矩阵就是稀疏矩阵。
我们在机器学习和深度学习中总会遇到很多稀疏问题。它们常出没于数据计数及单词编码,并且大多发生在自然语言处理领域中用tf-idf,word2vec等概念对单词进行矢量化处理时。
那么这是不是意味着,稀疏是个好东西?绝对不是!稀疏没啥大用,甚至还会帮倒忙。接下来,我们就来说说它带来的问题。
· 由于矩阵结构中存在大量的冗余0,稀疏矩阵的计算代价极高。这么多的0极大增加了空间的复杂性,让问题解决变得难上加难。规模的增加以及可能导致的各种资源缺乏会令机器学习算法效果大打折扣。
· 另一个重要问题是缩短了计算矩阵的有效时长,降低机器学习算法的计算处理速度。这会带来重大问题——整体上糟糕的,甚至是十分可怕的时间复杂度。这是都是更长的计算过程时间造成的。
假设我们有一个大且稀疏的矩X——这意味着与非零值相比,它有很多零,如下所示:

解决问题的主要思路是必须替代它们,因为零会增加时空的复杂性。得用各种代表非零值的键的字典(dok)或列表的列表(lil),过程如下:
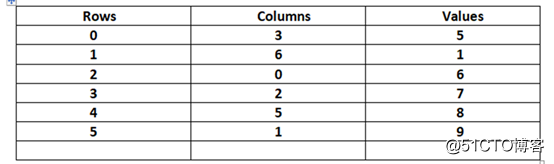
上表展示了解决此问题的绝妙方法。由此可以形成一个仅包含有用的非零数字的简化方程。下面的两种方法可以有效地表示稀疏矩阵:
· 压缩稀疏行:这种转换方法利用了上表的内容,即行和列的元组后面分别跟一个非零值来表示稀疏矩阵。
· 压缩稀疏列:这种转换方法利用了上表的内容,即列和行的元组后面分别跟一个非零值来表示稀疏矩阵。
压缩稀疏行(CSR)及压缩稀疏列(CSC)最能有效地表示稀疏矩阵。我更推荐CSR矩阵,而非CSC矩阵,因为我习惯用CSR了,并且它最标准。我也会使用Python中的scipy模块显示CSR和CSC转换的代码,选择适合自己的就好。
不多说理论了,撸起袖子直接编码!
开始吧!仅用numpy和scipy两个机器学习库就足矣计算上图的矩阵。可以使用简单的pip install命令安装这些文件。安装完成后,根据需要对矩阵进行构架并将其分配给变量。
下面的代码块代表了库的导入以及稀疏矩阵的创建过程,还有各个输出的图像。
import numpy as np
from scipy.sparse import csr_matrix
a =np.array([[0,0,0,5,0,0,0,0],
[0,0,0,0,0,0,1,0],
[6,0,0,0,0,0,0,0],
[0,0,7,0,0,0,0,0],
[0,0,0,0,0,8,0,0],
[0,9,0,0,0,0,0,0]])
print(a)
下一步是将该稀疏矩阵转换为压缩稀疏行(CSR)格式,输出类似于先前的表格,转换的代码块如下所示。另外,注意到该图中的(行,列)元组后跟都一个非零数字。
# Convert to CSR_Matrix
csr = csr_matrix(a)
print(csr)
若要将其转换回稀疏矩阵,则只需使用todense()函数,如下一个代码块所示:
# Convert back to dense matrix
dense =csr.todense()
print(dense)
若想知道如何对压缩的稀疏列矩阵进行相同的处理,看下一个代码块:
# Convert to CSC_Matrix
fromscipy.sparse import csc_matrix
csc =csc_matrix(a)
print(csc)
这就能说明所有的稀疏核心概念了。这样,我们就结束了关于稀疏性的讨论。稀疏矩阵在机器学习中极为常见,我们必须了解它们可能引起什么问题以及如何准确解决这些问题。
稀疏直觉必须有,要进行自然语言处理、计算机视觉项目、推荐系统以及任何数据中包含非零和零的数据的复杂任务时更应如此。这些不仅在机器学习中常见,在深度神经网络中也很常见。希望本文能帮你更好地了解稀疏和稀疏矩阵。
编译组:张天一、岳馨妍
相关链接:
https://towardsdatascience.com/lost-in-a-dense-forest-intuition-on-sparsity-in-machine-learning-with-simple-code-2b44ea7b07b0
如转载,请后台留言,遵守转载规范ACL2018论文集50篇解读
EMNLP2017论文集28篇论文解读
2018年AI三大顶会中国学术成果全链接
ACL2017论文集:34篇解读干货全在这里
10篇AAAI2017经典论文回顾长按识别二维码可添加关注
读芯君爱你

标签:alt 接下来 -o 理论 learn 遇到 owa 自己 结构
原文地址:https://blog.51cto.com/15057819/2564750