密码学-古典密码

标签：ext   word   加密   phi   for   spl   toc   public   移位   

代换密码

替换密码根据预先建立的替换表，将明文依次通过查表，替换为相应字符，生成密文，替换密码的密钥就是替换表。

单表代换

使用一个固定的替换表—明文、密文字符一一对应。

1. 移位密码

   \[??_??(??)＝(??＋??)\;??????\;??\; ＝\;??\quad0≤??, ??＜??，??＝ \lbrace ?? | 0≤??＜?? \rbrace \??_??(??)＝(??－??)\; ??????\; ??\;＝\;?? \]
   • 凯撒密码
     \[??_??(??)＝(??＋k)\;??????\;26\; ＝\;?? \??_??(??)＝(??－??)\; ??????\; 26\;＝\;?? \]

2. 乘数密码

   \[??_??(??)＝(??*k)\;??????\;q\; ＝\;?? \quad (k,q)=1\??_??(??)＝(??*??^{-1})\; ??????\; q\;＝\;?? \]

3. 仿射密码

   移位密码和乘数密码的结合。

   \[??_??(??)＝??*k_1+k_2\;??????\;q\; ＝\;?? \quad (k_1,q)=1\??_??(??)＝(??-??_{2})*k_1^{-1}\; ??????\; q\;＝\;?? \]

多表代换

使用多个替换表。

1. 一次一密

   每个明文字母都采用不同的替换表或密钥进行加密。

   实际应用中受限，主要因为

   • 密钥是真正的随机序列
   • 密钥长度＞明文长度
   • 每个密钥只使用一次

2. 维吉尼亚密码

   实质上是周期多表替换，减少了密钥量。

   置换表：

   

   明文映射到行，密钥映射到列，通过（明文，密钥）坐标查表可以输出密文。

   算法实现：

   • 替换表

   private static final String VIRGINIA_PASSWORD_TABLE_ARRAY[] = {"A","B","C","D","E","F","G","H","I","J","K","L","M","N","O","P","Q","R","S","T","U","V","W","X","Y","Z"};
   private static final List<String> VIRGINIA_PASSWORD_TABLE_ARRAY_LIST = Arrays.asList(VIRGINIA_PASSWORD_TABLE_ARRAY);
   

   • 判断字符串是否为空

   public static boolean isNotNull(Object object) {
           return Optional.ofNullable(object).isPresent();
       }
   public static boolean isStringNotEmpty(String str) {
           return isNotNull(str)&&!str.trim().equals("");
       }
   

   • 获取密钥集合

   private static List<Integer> getSecretKeyList(char[] secretCharArray, int length) {
           List<Integer> list = new ArrayList<Integer>();
           for (char c : secretCharArray) {
               int index = VIRGINIA_PASSWORD_TABLE_ARRAY_LIST.indexOf(String.valueOf(c).toUpperCase());
               list.add(index);
           }
   
   
           if(list.size()>length) {
               //截取和目标原文或密文相同长度的集合
               list = list.subList(0, length);
           }else {
               Integer[] keyArray = list.toArray(new Integer[0]);
               int keySize = list.size();
               //整除
               int count = length/keySize;
               for(int i=2;i<=count;i++) {
                   list.addAll(Arrays.asList(keyArray));
               }
               //求余
               int mold = length%keySize;
               if(mold>0) {
                   for(int j=0;j<mold;j++) {
                       list.add(keyArray[j]);
                   }
   
               }
           }
   
           return list;
       }
   

   • 维吉尼亚加密

   public static String virginiaEncode(String original,String secretKey) {
           if(isStringNotEmpty(secretKey)&&isStringNotEmpty(original)){
               char[] secretCharArray = secretKey.toCharArray();
               char[] originalCharArray = original.toCharArray();
               int length = originalCharArray.length;
   
               List<Integer> list = getSecretKeyList(secretCharArray, length);
   
               StringBuffer sb = new StringBuffer();
               for(int m=0;m<length;m++) {
                   char ch = originalCharArray[m];
                   int charIndex = VIRGINIA_PASSWORD_TABLE_ARRAY_LIST.indexOf(String.valueOf(ch).toUpperCase());
                   if(charIndex==-1) {
                       //不是26个英文字母的情况，原样加入
                       sb.append(ch);
                       continue;
                   }
   
                   int size = VIRGINIA_PASSWORD_TABLE_ARRAY_LIST.size();
                   //C = P + K (mod 26). 获取偏移量索引
                   int tmpIndex = (charIndex + list.get(m))%size;
                   sb.append(VIRGINIA_PASSWORD_TABLE_ARRAY_LIST.get(tmpIndex));
   
               }
               return sb.toString();
           }
           return null;
       }
   

   • 维吉尼亚解密

   public static String virginiaDecode(String cipherText,String secretKey) {
           if(isStringNotEmpty(cipherText)&&isStringNotEmpty(secretKey)) {
               char[] secretCharArray = secretKey.toCharArray();
               char[] cipherCharArray = cipherText.toCharArray();
               int length = cipherCharArray.length;
   
               List<Integer> list = getSecretKeyList(secretCharArray, length);
               StringBuffer sb = new StringBuffer();
               for(int m=0;m<length;m++) {
                   char ch = cipherCharArray[m];
                   int charIndex = VIRGINIA_PASSWORD_TABLE_ARRAY_LIST.indexOf(String.valueOf(ch).toUpperCase());
                   if(charIndex==-1) {
                       sb.append(String.valueOf(ch));
                       continue;
                   }
   
                   int size = VIRGINIA_PASSWORD_TABLE_ARRAY_LIST.size();
                   //P = C - K (mod 26). 模逆运算求索引
                   int len = (charIndex - list.get(m))%size;
                   //索引小于零，加模得正索引
                   int tmpIndex = len<0?len+size:len;
                   sb.append(VIRGINIA_PASSWORD_TABLE_ARRAY_LIST.get(tmpIndex));
   
               }
   
               return sb.toString();
           }
   
           return null;
       }
   

置换密码

明文字符集保持不变，但是顺序被打乱。

例：

安全性分析

穷举分析

移位密码穷举只需要\(n-1\)次。

乘数密码只需要$ \varphi(n)-1 $次。

放射密码只需要\(n\varphi(n)-1\)次。

统计特性分析

英语或者说任何自然语言都有固有的统计特性。可以根据字母频率进行破译。

同样，字母组合也有其统计特性。

可以根据其统计特性猜测置换的密文对应的明文。

单表替换统计分析

1. 统计密文的各种统计特征，如果密文量比较多，则完成这步后便可确定出大部分密文字母
2. 分析双字母、三字母密文组，以区分元音和辅音字母
3. 分析字母较多的密文，在这一过程中大胆使用猜测的方法，如果猜对一个或几个词，就会大大加快破译过程

多表替换统计分析

多表替换在一定程度上隐藏了明文消息的一些统计特性分析，破译相对比较困难。

• 主要包括两个步骤：

1. 确定密钥的长度d（就是确定使用的加密表个数）
2. 确定具体的密钥字

• 确定密钥的长度两种方法：

1. Kasiski测试法
2. 重合指数法

第一步：确定密钥字

Kasiski测试法基本原理

若用给定的d个密钥表周期地对明文字母加密，则当明文中两个相同字母组的间隔为d的倍数时，这两个明文字母组对应的密文字母组必相同

两个相同的密文段，对应的明文段不一定相同，但相同的可能性大。将密文中相同的字母组找出来，并找出相同字母组距离的最大公因子，就有可能提取出密钥的长度d

过程：

搜索长度至少为2的相邻的一对对相同的密文段，记下它们之间的距离。而密钥长度d可能就是这些距离的最大公因子。

重合指数法基本原理

重合指数：设\(x＝x_1\;x_2\;…\;x_n\)是n个字母的串，x的重合指数是指x中两个随机元素相同的概率，记为\(I_c ( x )\)

假定\(y＝y_1\;y_2\;…\;y_n\)是Vigenere密码的密文串。把\(y\)分成\(d\)个长为\(n/d\)的子串，记为\(Y_1, Y_2,?Y_d\)

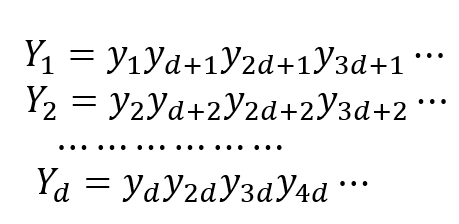
如果d是密钥字长度，那么每个\(Y_i\)都可以看作单表置换密码每个\(I_c(y_i)\;(1≤i≤d)\)都会趋近于0.065

如果不是，那么会更加随机一点。

维吉尼亚密码重合指数法分析密钥字长度：

public static int Friedman(String ciphertext) {
        int keyLength = 1; // 猜测密钥长度
        double[] Ic; // 重合指数
        double avgIc; // 平均重合指数
        ArrayList<String> cipherGroup; // 密文分组

        while (true) {
            Ic = new double[keyLength];
            cipherGroup = new ArrayList<>();
            avgIc = 0;

            // 1 先根据密钥长度分组
            for (int i = 0; i < keyLength; ++i) {
                StringBuilder tempGroup = new StringBuilder();
                for (int j = 0; i + j * keyLength < ciphertext.length(); ++j) {
                    tempGroup.append(ciphertext.charAt(i + j * keyLength));
                }
                cipherGroup.add(tempGroup.toString());
            }

            // 2 再计算每一组的重合指数
            for (int i = 0; i < keyLength; ++i) {
                String subCipher = cipherGroup.get(i); // 子串
                HashMap<Character, Integer> occurrenceNumber = new HashMap<>(); // 字母及其出现的次数

                // 2.1 初始化字母及其次数键值对
                for (int h = 0; h < 26; ++h) {
                    occurrenceNumber.put((char) (h + 65), 0);
                }

                // 2.2 统计每个字母出现的次数
                for (int j = 0; j < subCipher.length(); ++j) {
                    if(!Character.isLowerCase(subCipher.charAt(j)) && !Character.isUpperCase(subCipher.charAt(j)))
                        continue;
                    occurrenceNumber.put(subCipher.charAt(j), occurrenceNumber.get(subCipher.charAt(j)) + 1);
                }

                // 2.3 计算重合指数
                //double denominator = Math.pow((double) subCipher.length(), 2);
                double denominator = subCipher.length()*(subCipher.length()-1);
                for (int k = 0; k < 26; ++k) {
                    double o = (double) occurrenceNumber.get((char) (k + 65));
                    Ic[i] += o * (o - 1);
                }
                Ic[i] /= denominator;
            }

            // 3 判断退出条件,重合指数的平均值是否大于0.065
            for (int i = 0; i < keyLength; ++i) {
                avgIc += Ic[i];
            }
            avgIc /= (double) keyLength;
            if (avgIc >= 0.04) {
                break;
            } else {
                keyLength++;
            }
        } // while--end
    	 System.out.println("\n平均重合指数为： " + String.valueOf(avgIc));

       return keyLength;
}// Friedman--end

第二步：确定具体密钥字

这里已经退化成了凯撒密码，可以使用穷举法得到密钥字。

维吉尼亚密码确定密钥字：

public static String decryptCipher(int keyLength, String ciphertext) {
        int[] key = new int[keyLength];
        ArrayList<String> cipherGroup = new ArrayList<>();
        double[] probability = new double[]{0.082, 0.015, 0.028, 0.043, 0.127, 0.022, 0.02, 0.061, 0.07, 0.002, 0.008,
                0.04, 0.024, 0.067, 0.075, 0.019, 0.001, 0.06, 0.063, 0.091, 0.028, 0.01, 0.023, 0.001, 0.02, 0.001};

        // 1 先根据密钥长度分组
        for (int i = 0; i < keyLength; ++i) {
            StringBuilder temporaryGroup = new StringBuilder();
            for (int j = 0; i + j * keyLength < ciphertext.length(); ++j) {
                temporaryGroup.append(ciphertext.charAt(i + j * keyLength));
            }
            cipherGroup.add(temporaryGroup.toString());
        }

        // 2 确定密钥
        for (int i = 0; i < keyLength; ++i) {
            double maxMg=0;
            double MG; // 重合指数
            int flag; // 移动位置
            int g = 0; // 密文移动g个位置
            HashMap<Character, Integer> occurrenceNumber; // 字母出现次数
            String subCipher; // 子串

            while (g<26) {
                MG = 0;
                flag = 65 + g;
                subCipher = cipherGroup.get(i);
                occurrenceNumber = new HashMap<>();

                // 2.1 初始化字母及其次数
                for (int h = 0; h < 26; ++h) {
                    occurrenceNumber.put((char) (h + 65), 0);
                }

                // 2.2 统计字母出现次数
                for (int j = 0; j < subCipher.length(); ++j) {
                    if(!Character.isLowerCase(subCipher.charAt(j)) && !Character.isUpperCase(subCipher.charAt(j)))
                    {
                        continue;
                    }
                    occurrenceNumber.put(subCipher.charAt(j), occurrenceNumber.get(subCipher.charAt(j)) + 1);
                }

                // 2.3 计算重合指数
                for (int k = 0; k < 26; ++k,flag++) {
                    double p = probability[k];
                    flag = (flag >= 91) ? 65+((flag-65)%26) : flag;
                    //System.out.println("flag"+flag);
                    double f = (double) occurrenceNumber.get((char) flag) / subCipher.length();
                    MG += p * f ;
                }

                // 2.4 密钥字是值最大的那个
                if(MG>maxMg){
                    key[i] = g;
                    maxMg=MG;
                }
                g++;
            } // while--end
        } // for--end

        // 3 打印密钥
        StringBuilder keyString = new StringBuilder();
        for (int i = 0; i < keyLength; ++i) {
            keyString.append((char) (key[i] + 65));
        }
        //System.out.println("\n密钥为: " + keyString.toString());
        return keyString.toString();
    }

但是对于非已知密码算法可以采用重合互指数法。

重合互指数：假定\(x＝x_1\;x_2\;…\;x_n\)和\(y＝y_1\;y_2\;…\;y_n′\),分别是长为\(n\)和\(n‘\)的字母串。\(x\)和\(y\)的重合互指数是指\(x\)的一个随机元素等于\(y\)的一个随机元素的概率，记为\(MI_c(x,y)\)

具体步骤：

将\(x\)和\(y\)中的字母\(A,B,C,……,Z\)出现的次数分别表示为\(f_0,f_1,……,f_{25}\)和\(f_0^′, f_1^′,?, f_{25}^′\), 那么有

设定密钥字\(K=(k_1,k_2,k_3,...k_n)\)

\(MI_c (Y_i, Y_j )\)的估计值只依赖于差\((k_i－k_j) mod 26\)，我们称该差为\(Y_i\)和\(Y_j\)的相对移位。

当相对移位不是0，估计值在0.031-0.045之间，是0的时候，估计值是0.065。（我也不知道为啥）

可以利用这个计算出任何两个字串的\(Y_1,Y_2\)相对移位，有了相对移位只需要穷举26次就可找出密钥字。

密码学-古典密码

标签：ext   word   加密   phi   for   spl   toc   public   移位   

原文地址：https://www.cnblogs.com/fuao2000/p/14169453.html