二叉树

标签：idt   特性   定义   操作   code   特殊   集合   lazy   转换   

　　数据结构是一种特殊的组织和存储数据的方式，使我们可以更高效的对存储的数据执行操作。以下介绍常用的数据结构中的特殊树结构——二叉树。

　　二叉树是一种特殊的树结构，也是最常用的树结构，其存储和处理比一般树简单，一般树可以通过简单的转换得到与之对应的二叉树。

• 二叉树的定义：

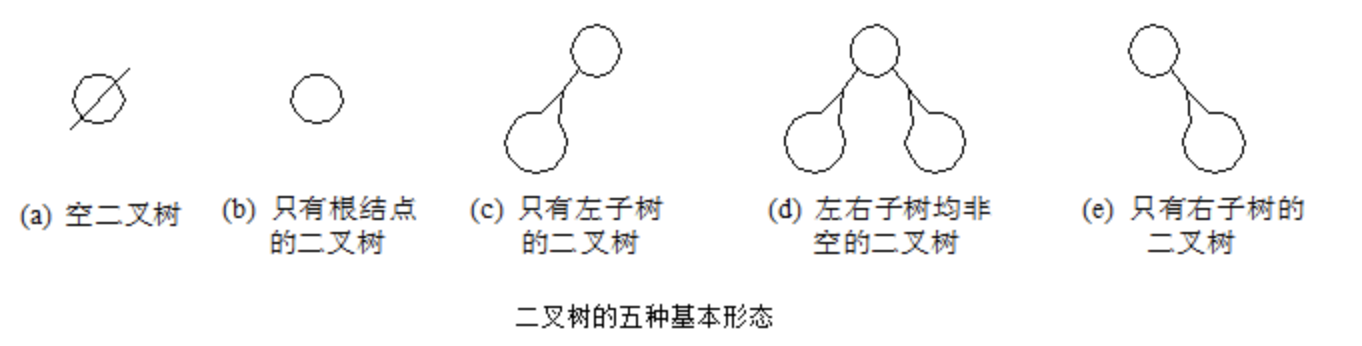
　　　　二叉树是n个结点所构成的集合，或为空树或为非空树。非空树T有：

• • 有且仅有一个称之为根的结点。
  • 除根结点以外的其余结点分为两个互不相交的子集T1和T2，分别为T的左子树和右子树，且T1和T2都是二叉树。
• 二叉树与树的区别：
  1. 二叉树的每个结点最多只有两棵子树；
  2. 二叉树的子树有左右之分，其次序不可颠倒。
• 二叉树的性质：
  • 在二叉树的第i层上最多有 2^i-1 个结点（ i >=1 ）。
  • 深度为k的二叉树最多有 2^K-1 个结点（ k >=1 ）。　
  • 对于任何一棵二叉树T，叶子数为N，度为2的结点数为M，有 N=M+1 。
• 满二叉树：

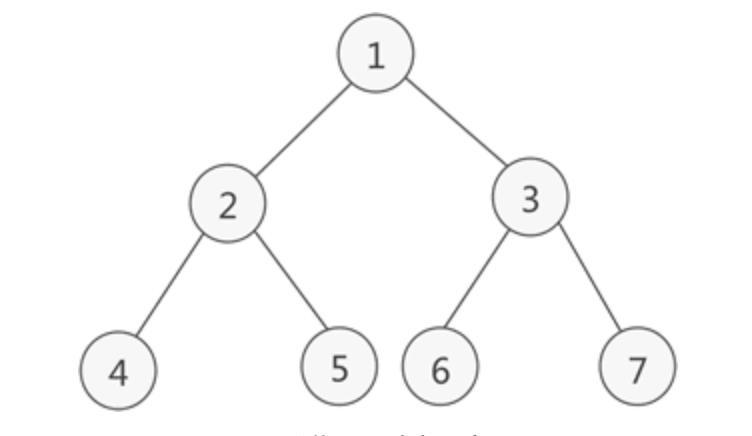
　　　如果二叉树中除了叶子结点，每个结点的度都为2，则此二叉树为满二叉树。

　　　满二叉树还有其特殊的性质：

• • 满二叉树中第i层上有 2^i-1 个结点。
  • 深度为k的满二叉树有 2^K-1 个结点，叶子数为 2^k-1
  • 满二叉树中不存在度为1的结点，每个分支点中都有两棵深度相同的子树，且叶子结点在最底层。
  • 具有n个结点的满二叉树的深度为 log₂(n+1)。　　　　　　

• 完全二叉树：

　　　如果二叉树中除去最后一层结点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树成为完全二叉树。　

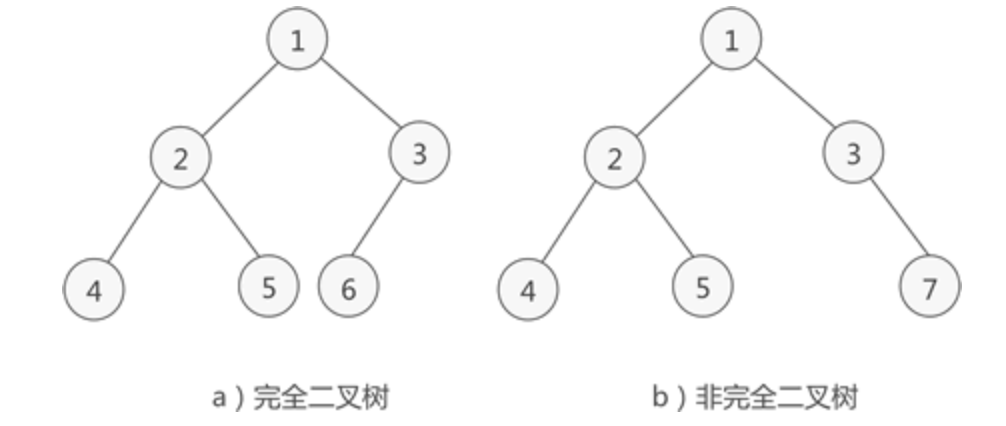
　　　　完全二叉树的特点：

• 1. 叶子结点只可能在层次最大的两层上出现；
  2. 对任一结点，若其右下分支下的子孙最大层次为L，则其左分支下的子孙的最大层次必为L或者L+1。

　　　　完全二叉树除了二叉树的3种性质外的独特性质：

• • 具有n个结点的完全二叉树的深度为：　 ?log₂n?+1　

　　　　　　（?log₂n? 表示取小于 log₂n 的最大整数。例如，?log₂4? = 2，而 ?log₂5? 结果也是 2。）　　　

• • 如果对一棵有n个结点的完全二叉树，对任一结点i，有

　　　　　　①如果i=1，则结点i是二叉树的根，无双亲。如果i>1,则其双亲的结点是 ?i/2?。

　　　　　　②如果2*i>n，则结点i为叶子结点。否则其左孩子的结点为2*i；

　　　　　　③如果2*i+1>n，则结点i肯定没有右孩子，否则其右孩子的结点为2*i+1。　　　　　　　　　　　　　　　

参考：https://mp.weixin.qq.com/s/rycQvasVNGcozyDiropSow、http://data.biancheng.net/view/23.html、http://data.biancheng.net/view/192.html

二叉树

标签：idt   特性   定义   操作   code   特殊   集合   lazy   转换   

原文地址：https://www.cnblogs.com/smallzhen/p/14176167.html