LeetCode 1672. 最富有客户的资产总量

标签：accounts   strong   str   ret   整数   解法   注释   eal   就是   

1672. 最富有客户的资产总量

难度·简单

给你一个 m x n 的整数网格 accounts ，其中 accounts[i][j] 是第 i 位客户在第 j 家银行托管的资产数量。返回最富有客户所拥有的 资产总量 。

客户的 资产总量 就是他们在各家银行托管的资产数量之和。最富有客户就是 资产总量 最大的客户。

示例 1：

输入：accounts = [[1,2,3],[3,2,1]]
输出：6
解释：
第 1 位客户的资产总量 = 1 + 2 + 3 = 6
第 2 位客户的资产总量 = 3 + 2 + 1 = 6
两位客户都是最富有的，资产总量都是 6 ，所以返回 6 。

示例 2：

输入：accounts = [[1,5],[7,3],[3,5]]
输出：10
解释：
第 1 位客户的资产总量 = 6
第 2 位客户的资产总量 = 10 
第 3 位客户的资产总量 = 8
第 2 位客户是最富有的，资产总量是 10

示例 3：

输入：accounts = [[2,8,7],[7,1,3],[1,9,5]]
输出：17

提示：

• m == accounts.length
• n == accounts[i].length
• 1 <= m, n <= 50
• 1 <= accounts[i][j] <= 100

题解

直接想到的是最简单的解法是双重遍历，具体见代码注释。

class Solution {
	public int maximumWealth(int[][] accounts) {
//		设res存放结果
		int res = 0;
//		双重循环遍历二维数组
		for (int i = 0; i < accounts.length; i++) {
//			设临时变量t存放每行元素之和
			int t = 0;
//			遍历行
			for (int j = 0; j < accounts[i].length; j++) {
//				累加行
				t += accounts[i][j];
			}
//			取max(res, t)
			res = Math.max(res, t);
		}
//		返回结果
		return res;
	}
}

时间复杂度：

\(O(mn)\)，其中m为行数，n为列数。

另外看到了另一种相似的解法：

class Solution {
	public int maximumWealth(int[][] accounts) {
		for (int i = 0; i < accounts.length; i++) {
			for (int j = 1; j < accounts[i].length; j++) {
				accounts[i][0] += accounts[i][j];
			}
			accounts[0][0] = Math.max(accounts[0][0], accounts[i][0]);
		}
		return accounts[0][0];
	}
}

这种写法是不额外设置新变量存放结果，而是直接用现有数组的空闲位置作为存储空间，可以省出两个额外的变量空间。表面上看的确如此，但是通过测试发现，两种写法对内存的消耗基本一致。

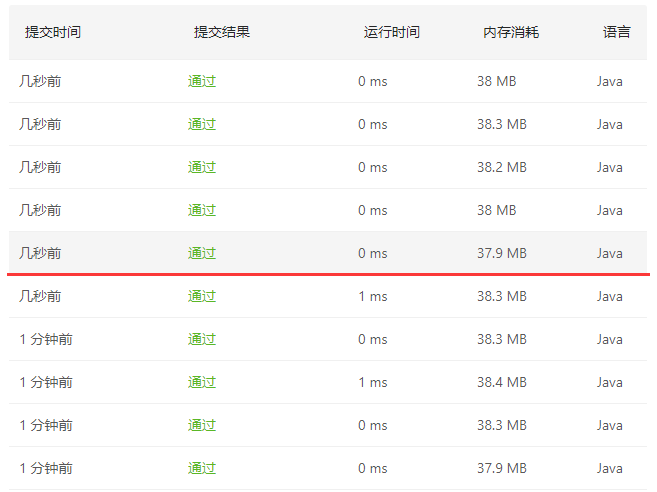
红线之上的是第一种借助变量存放结果的写法，红线之下的是第二种直接利用数组空间存放结果的写法，通过数据上的表现来看，第二种写法的平均时间消耗和平均内存消耗甚至不如第一种写法，或许这是由于LeetCode的判题机制导致的，或许是有其他原因。

也许其他原因包含底层的JVM处理优化的结果，但我想这或许依然是奥卡姆剃刀定律的表现，往往简单的方法在简单的结构上会发挥的更高效。

LeetCode 1672. 最富有客户的资产总量

标签：accounts   strong   str   ret   整数   解法   注释   eal   就是   

原文地址：https://www.cnblogs.com/biem/p/14191639.html