标签:sizeof 代码 问题 使用 bcd ++ type img zcat
哈夫曼编码是一种变长编码,根据字符频率确定编码的长度。在学习数据结构时,我们知道,通过贪心的策略自底向上构造二叉树,最后得到哈夫曼树。从根节点遍历,便可以得到编码。
本文给出了经典教材《数据结构》一书上算法6.12的具体实现细节。
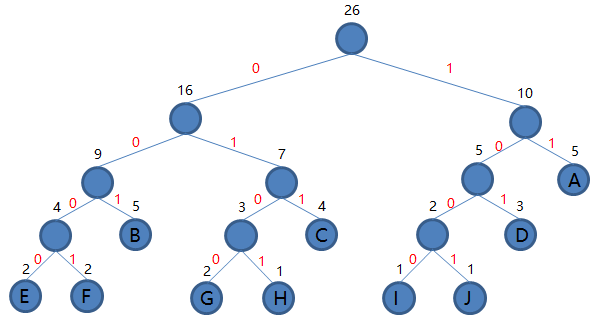
构造二叉树的过程为:初始为全部字符的 \(n\) 个叶子节点,每次选择权值最小的两个根节点合并,形成新的节点,其权值为合并的两节点权值之和。引入 parent 作为是否为根节点判断的标志。
\(n\) 个节点完成 \(n-1\) 次合并操作,形成共包含 \(2n-1\) 个节点的二叉树,树的根节点编号为 \(2n-1\) 。
// 哈夫曼树节点类型
typedef struct {
char data; // 节点字符
double weight; // 节点权值
int parent, lchild, rchild; // 父节点、左右孩子节点
}HfmTNode, *HuffmanTree;
// 哈夫曼编码类型 记录{字符 -> 编码}
typedef struct {
char letter; // 节点字符
char *code; // 节点编码
}HfmCNode, *HuffmanCode;
// 哈夫曼类型
typedef struct {
HuffmanTree tree;
HuffmanCode code;
int n; // 字符集长度
char *letters; // 字符集
int *frequency; // 字符频率
int rt; // 哈夫曼树根节点编号,根节点即 `tree[2n-1]`
}Huffman;
参考 《数据结构(C语言版)》
P147 算法 6.12
要得到哈夫曼编码,依次调用
// 初始化哈夫曼
void initHuffman(Huffman *hfm, const char *letters, const int frequency[], int n)
{
if (n<1) return;
int m = 2*n-1;
hfm->n = n;
hfm->letters = (char*)malloc((n+1)*sizeof(char));
hfm->frequency = (int*)malloc((n+1)*sizeof(int));
hfm->tree = (HuffmanTree)malloc((m+1)* sizeof(HfmTNode));
hfm->rt = m;
for (int i=1;i<=n;i++)
{
hfm->letters[i] = letters[i-1];
hfm->frequency[i] = frequency[i-1];
}
for (int i=1;i<=n;i++)
hfm->tree[i] = (HfmTNode){letters[i-1], frequency[i-1], 0, 0, 0};
for (int i=n+1;i<2*n;i++)
hfm->tree[i] = (HfmTNode){0, 0, 0, 0, 0};
for(int i=n+1;i<=m;i++)
{
hfm->tree[i].weight = 0;
hfm->tree[i].lchild = hfm->tree[i].rchild = hfm->tree[i].parent = 0;
}
}
// 建立哈夫曼树
void buildHuffmanTree(Huffman *hfm)
{
// 建立哈夫曼树
int n = hfm->n;
int m = 2*n-1;
for(int i=n+1;i<=m;i++)
{
int p1 = 1, p2 = 1; // p1记录最小结点位置, p2记录第二小
while(p1<=i-1 && hfm->tree[p1].parent) p1++;
p2 = p1+1;
while(p2<=i-1 && hfm->tree[p2].parent) p2++;
for(int j=p1+1;j<=i-1;j++)
{
if (hfm->tree[j].parent) continue; // 非根节点
if(hfm->tree[j].weight<=hfm->tree[p1].weight)
{
p2 = p1, p1 = j;
}
else if(hfm->tree[j].weight<hfm->tree[p2].weight)
{
p2 = j;
}
}
hfm->tree[i].weight = hfm->tree[p1].weight + hfm->tree[p2].weight;
hfm->tree[i].lchild = p1; hfm->tree[i].rchild = p2;
hfm->tree[p1].parent = i; hfm->tree[p2].parent = i;
}
}
// 获取哈夫曼编码
void getHuffmanCode(Huffman *hfm)
{
// 求赫夫曼编码
int n = hfm->n;
hfm->code = (HuffmanCode)malloc((n+1)*sizeof(HfmCNode));
for (int i=1;i<=n;i++) hfm->code[i] = (HfmCNode){hfm->letters[i], ""};
char *code = (char *)malloc(n*sizeof(char));
code[n-1] = ‘\0‘;
for(int i=1;i<=n;i++)
{
int start = n-1;
int c = i, f = hfm->tree[i].parent;
while(f)
{
if(c==hfm->tree[f].lchild) code[--start] = ‘0‘;
else code[--start] = ‘1‘;
c = f; f = hfm->tree[c].parent;
}
hfm->code[i].code = (char*)malloc((n-start)*sizeof(char));
strcpy(hfm->code[i].code, &code[start]);
}
free(code);
}
// 凹入表示法输出
void showHuffmanTree(Huffman *hfm, int rt=-1, int level=0)
{
if (rt==0) return ;
if (rt==-1)
{
printf("HuffmanCode:\n");
for (int i=1;i<=hfm->n;i++)
{
// printf("%c\n", hfm->letters[i]);
// printf("%c\n", hfm->tree[i].data);
printf("%c:%s\n", hfm->code[i].letter, hfm->code[i].code);
}
rt = hfm->rt;
printf("HuffmanTree:\n");
}
int i;
for(i=0;i<level;i++) printf(" ");
if (hfm->tree[rt].data==0)
printf("**\n");
else
printf("%c:%s\n", hfm->tree[rt].data, hfm->code[rt].code);
showHuffmanTree(hfm, hfm->tree[rt].lchild, level+1);
showHuffmanTree(hfm, hfm->tree[rt].rchild, level+1);
}
图方便,直接使用了C++ string类型,而不是基于C类型字符串(本质上是 char*字符数组)
// 编码
string Encode(Huffman *hfm, const char *input)
{
int cnt = 0;
string output = "";
for (int i=0;input[i];i++)
{
char c = input[i];
for (int i=1;i<=hfm->n;i++)
{
if (hfm->code[i].letter==c)
{
output += hfm->code[i].code;
break;
}
}
if (++cnt<=10)
cout<<output<<endl;
}
return output;
}
// 译码
string Decode(Huffman *hfm, const char *input)
{
int p = hfm->rt;
string output = "";
for (int i=0;input[i];i++)
{
char c = input[i];
if(c==‘0‘) p = hfm->tree[p].lchild;
else p = hfm->tree[p].rchild;
if(p<=hfm->n) // 翻译到叶子节点
{
output += hfm->tree[p].data;
p = hfm->rt;
}
}
return output;
}
// 统计文章字符频率 建立哈夫曼树
void readTxt2Huffman(const char *filename, Huffman *hfm)
{
FILE *fp = fopen(filename, "r");
if (fp==NULL) return;
char *letters = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ ,.;\‘\"";
int frequency[58] = {0}; // 2*26个字母 空格 逗号 句号 分号 单引号 双引号
while(1)
{
char c = fgetc(fp);
if (feof(fp))
break;
// if (c>=‘a‘ && c<=‘z‘) c += ‘A‘ - ‘a‘;
if (c>=‘a‘ && c<=‘z‘) frequency[c-‘a‘]++;
else if (c>=‘A‘ && c<=‘Z‘) frequency[c-‘A‘+26]++;
else if (c==‘ ‘) frequency[52]++;
else if(c==‘,‘) frequency[53]++;
else if(c==‘.‘) frequency[54]++;
else if(c==‘;‘) frequency[55]++;
else if(c==‘\‘‘) frequency[56]++;
else if(c==‘\"‘) frequency[57]++;
// else printf("%c\n", c);
}
initHuffman(hfm, letters, frequency, 58);
buildHuffmanTree(hfm);
getHuffmanCode(hfm);
}
// 读文件,返回char*字符串
char* readText(const char* filename)
{
char* text;
FILE *pf = fopen(filename, "r");
if (pf==NULL)
{
printf("文件%s不存在\n", filename);
return "";
}
fseek(pf, 0, SEEK_END);
long lSize = ftell(pf);
text = (char*)malloc(lSize+1);
rewind(pf);
fread(text, sizeof(char), lSize, pf);
text[lSize] = ‘\0‘;
return text;
}
int main()
{
/*
Huffman hfm;
int w[6] = {1, 2, 3, 4, 6, 8};
initHuffman(&hfm, "abcdef", w, 6);
buildHuffmanTree(&hfm);
getHuffmanCode(&hfm);
for (int i=1;i<=6;i++)
{
printf("%c\n", hfm.letters[i]);
printf("%c\n", hfm.tree[i].data);
printf("%s\n", hfm.code[i].code);
}
showHuffmanTree(&hfm);
cout<<Encode(&hfm, "bacbefd")<<endl;
cout<<Decode(&hfm, "100110001011001011100")<<endl;
*/
// 测试读文件,完成编码,译码
const char *filename = "article.txt";
Huffman hfm;
readTxt2Huffman(filename, &hfm);
showHuffmanTree(&hfm);
char text[5000];
strcpy(text, readText(filename));
// printf("加密前:\n");
// printf("%s\n", text);
// printf("加密后:\n");
string text_encode = Encode(&hfm, text);
cout<<text_encode<<endl;
cout<<Decode(&hfm, text_encode.c_str())<<endl;
return 0;
}
任务一需要从控制台读入 需要按Ctrl Z终止输入 用 2==scanf()跳出循环
分配内存使用malloc,单块内存大小为 sizeof(xxx) 写错了类型,导致程序无输出也没有报错,花费很长时间才定位到错误
hfm->code = (HuffmanCode)malloc((n+1)*sizeof(HfmCNode))
读取文章能正常建立哈夫曼树并编码 ,译码过程出错。通过输出译码过程,检查到字符集(包含小写)与译码规则不一致,需要对大小写特判。完善字符集,包含大小写和各种符号的字符集作为输入,便可直接译码得到原始输入。
本人学习《数据结构》这门课是在大一C语言刚结束之后,彼时对C语言的核心——指针还没完全琢磨透彻。学习数据结构也仅仅按部就班完成了书上的课程实验,现在回头看过去写的代码,不仅代码风格凌乱,也存在内存泄漏的隐患。本次帮学弟写作业的同时,顺便重构了过去的代码。最近需要用C/C++进行k-means的算法优化,也借此好好熟悉一番传统的C/C++。
(完)
标签:sizeof 代码 问题 使用 bcd ++ type img zcat
原文地址:https://www.cnblogs.com/izcat/p/14193102.html