标签:它的 导出 需要 code 旋转矩阵 begin 假设 loading image
最近有一个需求是已知一个变换矩阵,如何根据该矩阵获取它的位移、旋转和缩放参数?
这个问题当初书里没直接讲,但是可以通过已有的知识推导出来。
首先我们知道,图形学中的变换一般有三种:缩放、旋转和位移,它们均可以用4*4的方阵予以表达。
比如缩放矩阵的形式如下:
\(\begin{bmatrix} sx & 0 & 0 & 0 \\ 0 & sy & 0 & 0 \\ 0 & 0 & sz & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\)
位移矩阵的形式如下:
\(\begin{bmatrix} 1 & 0 & 0 & tx \\ 0 & 1 & 0 & ty \\ 0 & 0 & 1 & tz \\ 0 & 0 & 0 & 1 \end{bmatrix}\)
旋转矩阵则比较复杂,绕着uvw轴(两两正交且长度为1)转θ的矩阵如下:
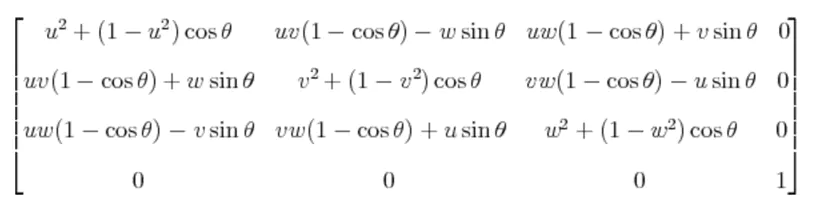
我们又知道,在图形学中,可以通过矩阵相乘的方式来将各种变换操作叠加,常见的就是SRT,也就是将缩放、旋转、平移三个矩阵乘在一起组合为新矩阵,用以表达一个物体总的变换。
那么,假设我们已知一个SRT矩阵,又该如何分解出其中的S、R和T呢?
其实仔细想一下也是比较简单的,首先平移的部分始终位于矩阵的最后一列,可直接取出:
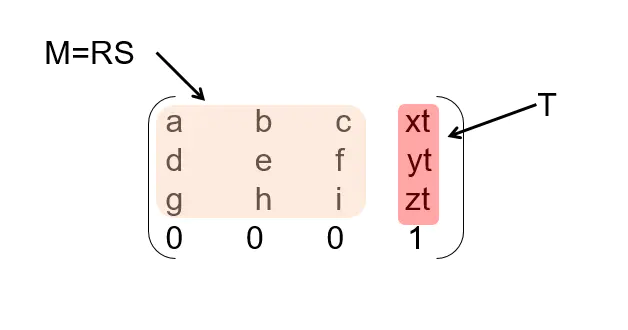
接下来,该矩阵的3*3部分是SR矩阵相乘的结果,我们又该如何进一步提取呢?
回想一下,三维旋转矩阵本身需要满足正交矩阵的性质,也就是它的每一行和每一列长度均要为1,我们可以从这一点入手,计算出该矩阵SR部分每一行的长度,它就一定是x、y、z轴的缩放!
然后再将SR部分的每一行除以sx、sy、sz就可以得到R矩阵了!
标签:它的 导出 需要 code 旋转矩阵 begin 假设 loading image
原文地址:https://www.cnblogs.com/wickedpriest/p/14198547.html