标签:想法 效率 执行 一个 电影 它的 插入 avl树 二叉搜索树
前几天学习容器map时,看到说明,说map是采用红黑树实现的,于是就查了红黑树,不查不知道,一查一大跳,原来这玩意那么重要。然而我本科好像没学过,也可能老师讲过只是我没听。于是出于好奇就学了一下。下文详细介绍自己的学习过程与学习所得。红黑树遍历过程如下。
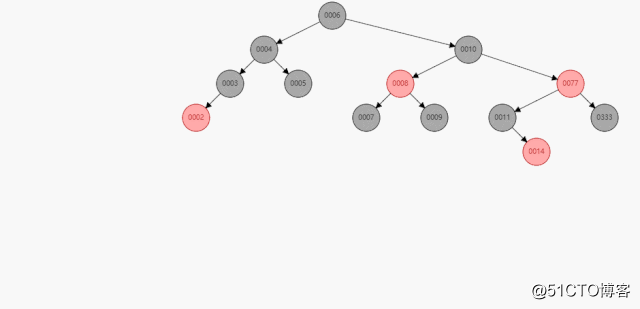
1.红黑树的相关概念
Red-Black Tree 称为“红黑树”,是一种自平衡二叉查找树,红黑树和 AVL 树类似,在进行插入和删除时需要通过旋转和重新着色来维持其红黑树的特性。
红黑树的应用相当广泛,主要是用它来存储有序的数据,它的时间复杂度为 O(logn),查询效率非常高。
下面讲一下其具体定义与性质
其具体定义为:是一种含有黑红结点并且能自平衡的二叉查找树
依据其定义可知其特征:结点有两种颜色,能自平衡,是二叉查找树。
二叉查找树如下图所示:
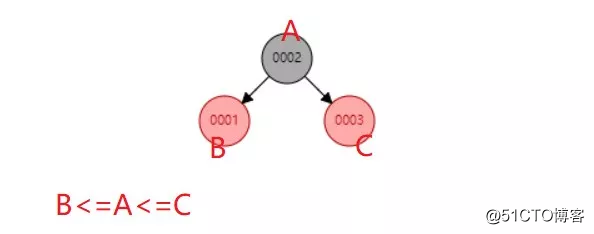
红黑树性质如下:括号内的为自己的想法
性质1:结点有且仅有红黑两种颜色
性质2:根结点为黑色
性质3:每个叶子结点(NIL)是黑色(这里的叶子结点需要格外注意与正常树的区别,此处的是假想出来的)
性质4:红色结点的子结点是黑色(反推红色结点的父结点为黑色)
性质5:任意一个结点到每个叶子结点的路径包含相同数量的黑色结点
2.红黑树的性质讲解
关于性质1:性质1没啥好说的,就是红黑两种颜色
关于性质2:根节点为黑色。假设一个树只有根节点,且根节点是红色。此时你会发现,此树符合红黑树定义的性质1、3、4、5.因此呢,根节点是黑色是硬性规定,没必要去深究理解。
关于性质3:每个叶子结点是黑色的用下图解释
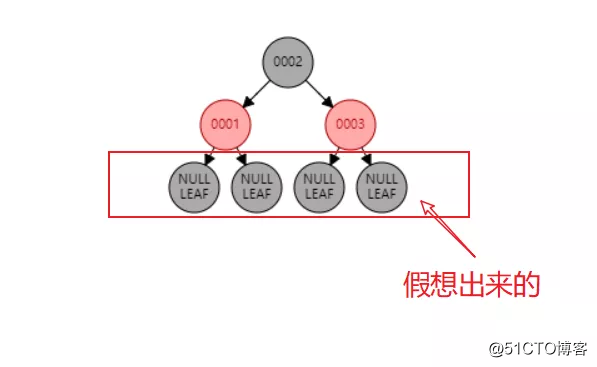
其中假想出来的叶子结点具有以下特征:颜色为黑色,值是NULL。
关于性质4:红色结点的子结点是黑色,下图可以说明。
由于红色结点的子结点是黑色,所以红色结点的父结点是黑色(可以利用假设法证明)。关于001这种红色结点,他的两个子结点为两个黑色叶子结点NIL。
关于性质5:任意一个结点到每个叶子结点的路径包含相同数量的黑色结点用下图说明。
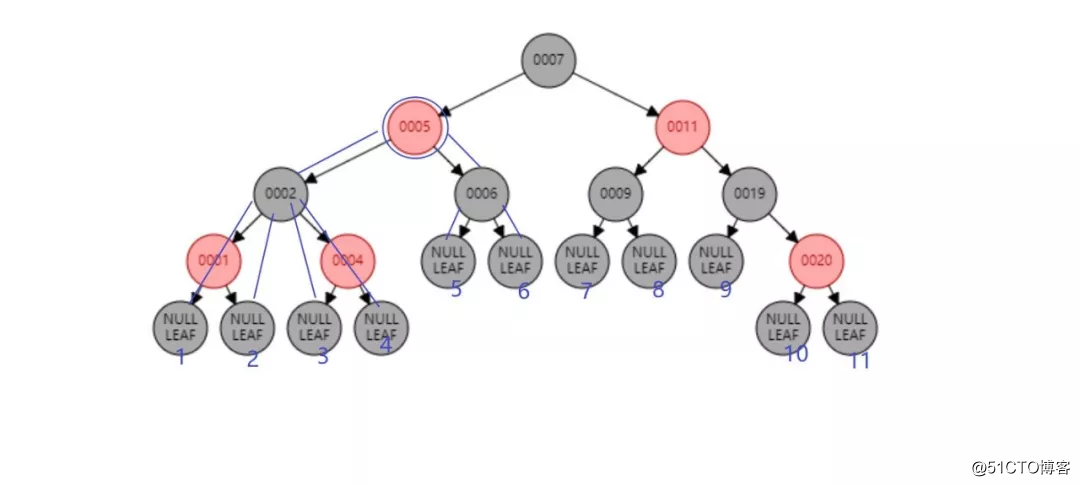
从图中你可以看到,从005到1-6六个叶子结点都只路过一个黑色结点。同理其他结点可证。
下面说一下自己关于这个性质的理解。
如果把红黑树的红色结点全部抹掉,你会发现他是一个完全黑色平衡的树(黑色结点的层级完全一样)
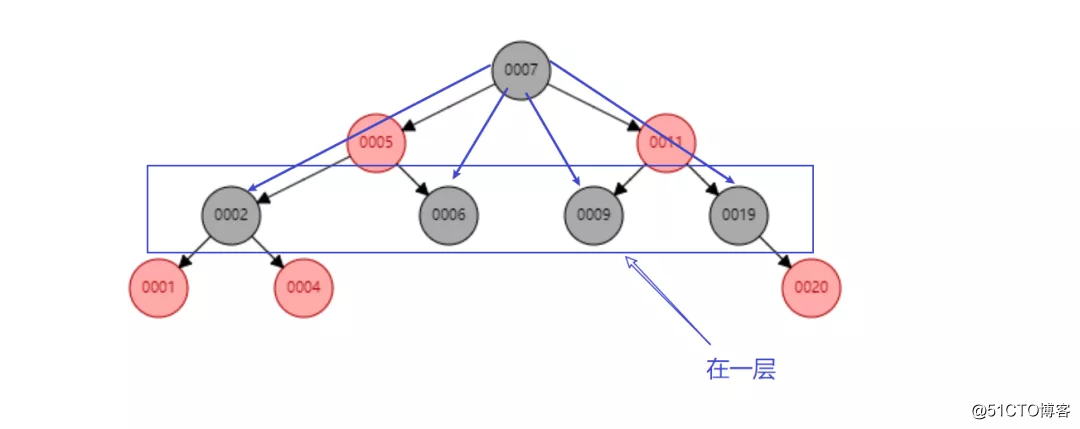
因此网上给红黑树的定义为:非完美平衡二叉查找树,是完美黑色平衡二叉查找树。
3.红黑树的操作
说了那么多最后还是要去操作,操作无非就是增删改查。在讲解操作之前,讲一下红黑树的自平衡最小单元。
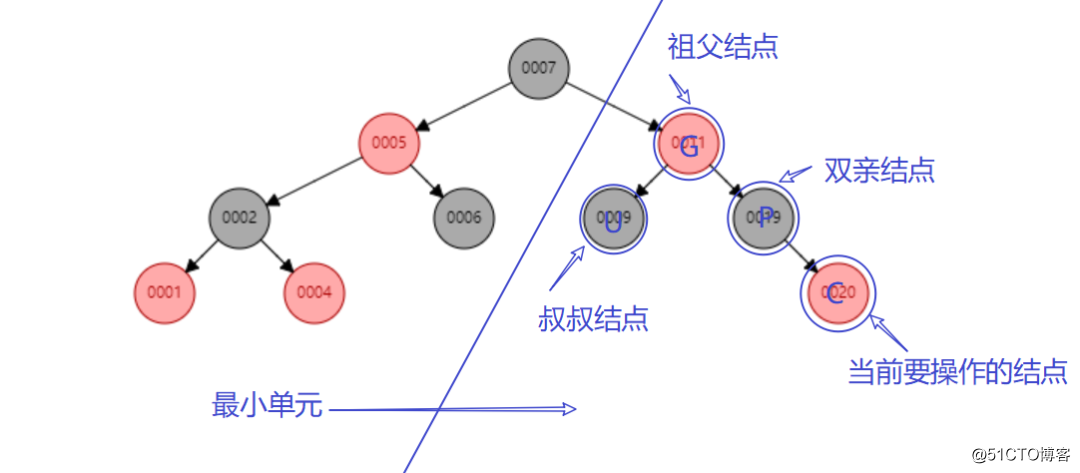
3.1查找操作
红黑树查找操作和二叉搜索树完全一致:根据结点值一一匹配。下图为查找14的过程。
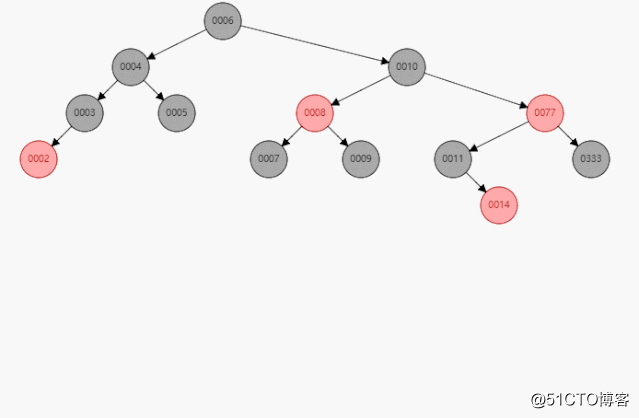
3.2新增操作
红黑树的新增操作包括两步:变色、旋转。变色没什么好说,根据原则变色即可,旋转和AVL树的旋转一致。关于左右旋网上一大堆在这里就不讲了。
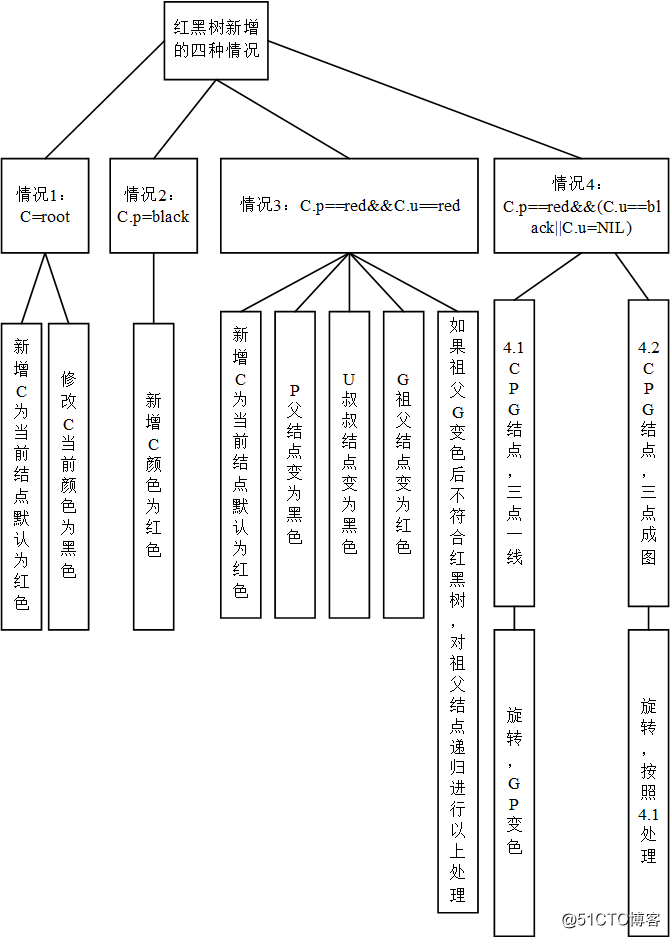
以上就是关于红黑树的新增操作。
演示如下。

3.3删除操作
将红黑树内的某一个节点删除。需要执行的操作依次是:
将红黑树当作一颗二叉查找树,将该节点从二叉查找树中删除
欢迎访问电影小程序
标签:想法 效率 执行 一个 电影 它的 插入 avl树 二叉搜索树
原文地址:https://blog.51cto.com/15069472/2577275