标签：library ant data 转化 port mil 理论 reject 单位
计数和分类变量是我们经常遇到的，比如一个群体中患病个体数、等位基因频数等。不少人习惯把计数变量转换成比率来进行分析。但是，这么做存在很大的问题。10/20和1/2在数值上是相等的，但是它们的样本数量却不一样，如果转换成比率来分析，实际上就损失掉了样本量。所以，并不推荐将计数资料转换成比例来分析。那么对于计数和分类资料怎么分析呢？本章就来一探究竟。
二项回归模型binomial regression: 即变量只有两个结果 - 如死亡/存活，接收/拒绝，左边/右边等。
【温馨提示：代码块可左右滑动】
二项分布的表示：
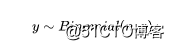
其中，y是非负整数，p是每次试验某一结果发生的概率，n是试验的次数。
在拟合二项回归模型时，通常有两种数据形式，一种是针对每一个个体的数据，比如是否患病，通常用0和1来表示，这种回归也称之为logistic回归；另一种数据形式是汇总所有的结果，比如一个群体一个有100个个体患病。这两种形式都可以用来拟合二项回归模型，对结果没有影响。下面以具体例子来展示两种不同数据形式的二项回归模型。
本例子来自对黑猩猩社交倾向的实验。一只黑猩猩坐在一个长桌子的一端，面前有两个操纵杆，一个位于左手边，一个位于右手边。桌子中间摆着四个盘子，其中三个盘子里面放着食物（两个位于黑猩猩这边，另一个位于远端），见下图。左侧两个盘子连着左侧操作杆，右侧两个盘子连着右侧操作杆。当黑猩猩按下左侧操作杆时，左侧位于桌子中间的两个盘子及其中的食物会移向桌子的两端；按下右侧操作杆时，右侧同样如此。所以，不管黑猩猩按下哪一个操纵杆，它本身都会得到盘子里面的食物，但是如果长桌子另一端有另一只猩猩，该猩猩不一定每次都能获得食物，有可能会是一个空盘子。
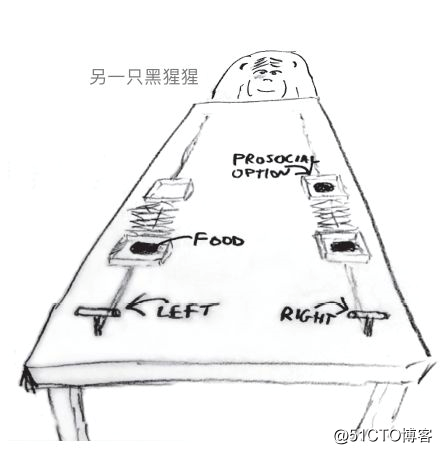
所以该实验有两种情景，一种是桌子远端没有另一只黑猩猩；另一种情况是桌子远端有另一只黑猩猩（如上图）。如果是用人来做这个实验，如果桌子对面有另一个人存在，那么被试者几乎全部选择按下有两份食物的操作杆，被试者和另一个人都能得到食物，也就是人的社交倾向。那么如果是用黑猩猩来做这个实验呢？
下面就是用黑猩猩做上述实验的数据
library(rethinking)
data(chimpanzees)
d <- chimpanzees
head(d)## actor recipient condition block trial prosoc_left chose_prosoc
## 1 1 NA 0 1 2 0 1
## 2 1 NA 0 1 4 0 0
## 3 1 NA 0 1 6 1 0
## 4 1 NA 0 1 8 0 1
## 5 1 NA 0 1 10 1 1
## 6 1 NA 0 1 12 1 1
## pulled_left
## 1 0
## 2 1
## 3 0
## 4 0
## 5 1
## 6 1pulled_left是我们的结果变量，0和1表示该被试猩猩是否按下左侧操作杆；prosoc_left和condition是自变量。prosoc_left的数值也是0和1，表示左侧操作杆是否连有两份食物，1表示左侧操作杆连有2份事物，0表示只有一份食物，表示黑猩猩的社交倾向；condition表示长桌对面是否有另一只猩猩，1表示有，0表示没有（对照）。
将上述1个因变量和2个自变量拟合为二项回归模型，为：
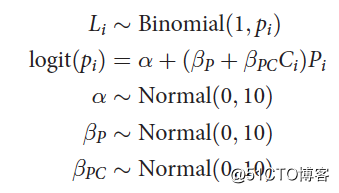
其中，L表示pulled_left；P表示prosoc_left；C表示condition。上述模型考虑了交互作用。其他几个参数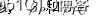
的先验分布为弱信息的正态分布。根据之前文章的介绍，弱信息先验概率会导致过度拟合，所以为了评估过度拟合的程度，我们又建立了两个参数较少的模型。第一个仅包含截距项：
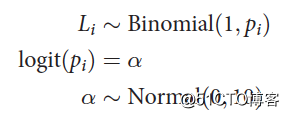
第二个包含截距项和社交倾向变量，没有包括condition:
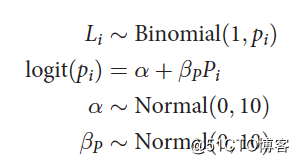
在R语言中，我们对第一个截距模型进行拟合：
m10.1 <- map(
alist(
pulled_left ~ dbinom(1,p),
logit(p) <- a,
a ~ dnorm(0,10)
),
data = d
)
precis(m10.1)## Mean StdDev 5.5% 94.5%
## a 0.32 0.09 0.18 0.46在对截距进行解释之前，我们还要对其进行logistic转换，因为我们拟合的模型中，因变量都是进行了logit转换的，通过rethinking::logistic进行逆转换，将截距变为原始量纲。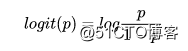
logistic(c(0.18,0.46))## [1] 0.5448789 0.6130142也就是说，在没有考虑任何自变量的情况下，黑猩猩有更大的可能性按左侧的操作杆。
同样地，我们拟合第二个包含截距项和社交倾向变量的模型，以及包含全部两个自变量的模型。
对三个模型进行比较，如下：
m10.2 <- map(
alist(
pulled_left ~ dbinom(1,p),
logit(p) <- a + bp*prosoc_left,
a ~ dnorm(0,10),
bp ~ dnorm(0,10)
),
data = d
)
m10.3 <- map(
alist(
pulled_left <- dbinom(1,p),
logit(p) <- a + (bp + bpC * condition)*prosoc_left,
a ~ dnorm(0,10),
bp ~ dnorm(0,10),
bpC ~ dnorm(0,10)
),
data = d
)
compare(m10.1,m10.2,m10.3)## WAIC pWAIC dWAIC weight SE dSE
## m10.2 680.3 1.9 0.0 0.70 9.28 NA
## m10.3 682.2 2.9 1.8 0.28 9.30 0.85
## m10.1 688.0 1.0 7.7 0.02 7.11 6.13通过比较发现，包含所有2个自变量的模型（m10.3)并不是最好的一个，其WAIC值比m10.2模型要大。为什么m10.3模型不好呢？
具体看一下m10.3模型的参数估计值：
precis(m10.3)
其中交互作用bpC的估计区间是一个包括0的很宽大的区间，也就是受试黑猩猩选择按下左侧操作杆还是右侧操作杆并不受对面是否存在另一只猩猩的影响，而且受试黑猩猩总是习惯与按下连有两份食物的操作杆（bp=0.61）。
那么怎么理解bp=0.61？首先我们要区分两个概念，一个是绝对效应，另一个是相对效应。绝对效应是所有自变量导致的因变量的变化大小；而相对效应是一个自变量的变化导致因变量变化的占比大小。由于相对效应忽略了其他变量的影响，常常会误导人们。
首先我们来看prosoc_left和它的参数bp的相对效应。在logistic模型中，其相对效应也称之为风险比的变化大小。其中风险比是一件事发生的可能性大小与不发生可能性大小的比值，即p/(1-p)。如果自变量prosoc_left的值从0变为1，那么根据参数bp的大小我们可以判定，按左侧操作杆的对数风险比增加了0.61。注意这里是对数风险比，我们把它还原为原始形式为：
exp(0.61)## [1] 1.840431也即是说，prosoc_left从0变为1，实际风险比增加了84%。
不过其实际意义，或者说其绝对效应的大小还取决于截距项。如果截距项足够大，几乎确定受试黑猩猩会按下左侧操作杆，那么风险比即便增加84%也显得无不足道。如截距 = 4，那么：
logistic(4)## [1] 0.9820138也就意味着黑猩猩有98.2%的可能性会按下左侧操作杆，此时如果风险比增加84%：
logistic(4 + 0.61)## [1] 0.9901462可以看到，按下左侧操作杆的概率增加了不到1%！同样地，如果截距是个绝对值很大的负值，风险比即便增加84%，也可能最后实际概率依旧很小。所以在使用相对效应（风险比）的时候一定要注意，避免被误导。
为了更直观的展现上述结果，将m10.3模型的2个二分类变量（4种组合形式）进行作图，如下：
d.pred <- data.frame(
prosoc_left = c(0,1,0,1),
condition = c(0,0,1,1)
)
chimp.ensemble <- ensemble(m10.1,m10.2,m10.3, data = d.pred)
# head(chimp.ensemble)
pred.p <- apply(chimp.ensemble$link,2,mean)
pred.p.PI <- apply(chimp.ensemble$link,2,PI)
#作图
plot(0,0, type = "n", xlab = "prosoc_left/condition",
ylab = "proportion pulled left", ylim = c(0,1),
xaxt = "n", xlim = c(1,4))
axis(1,at=1:4, labels = c("0/0","1/0","0/1","1/1"))
p <- by(d$pulled_left, list(d$prosoc_left, d$condition,d$actor), mean)
for(chimp in 1:7)
{
lines(1:4, as.vector(p[,,chimp]), col=rangi2, lwd = 1.5)
}
lines(1:4, pred.p)
shade(pred.p.PI,1:4)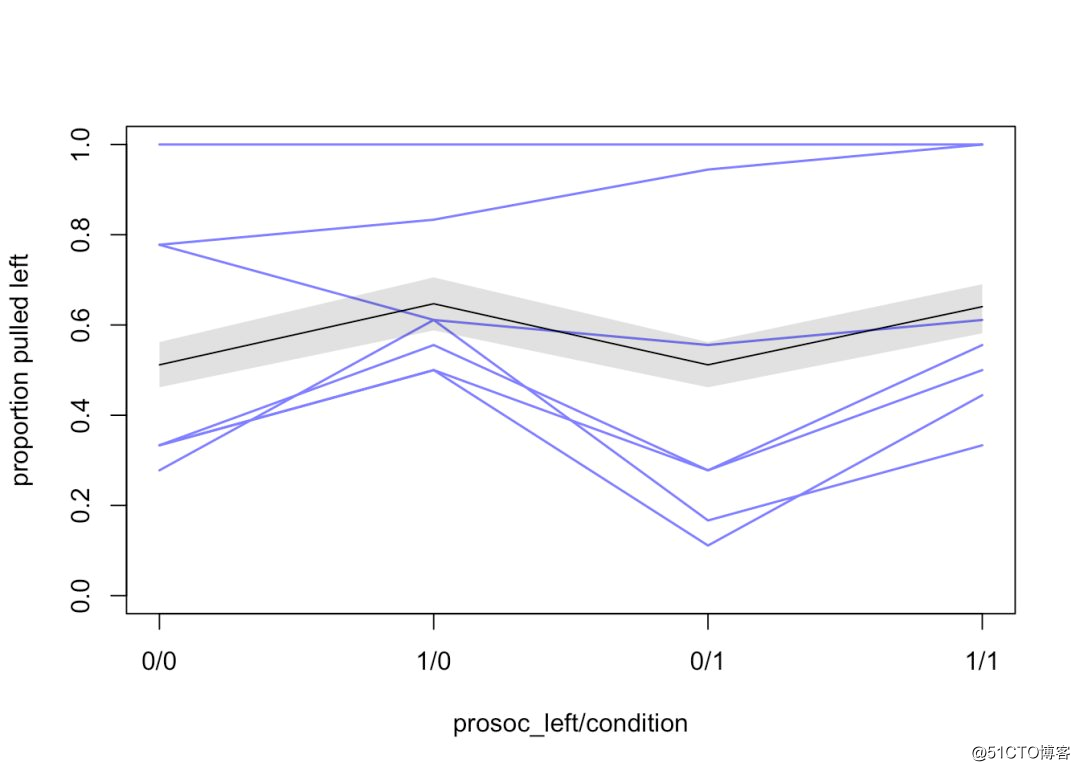
其中的7条蓝线表示7个受试个体（黑猩猩）多次试验的平均值。黑线表示全部7个受试个体的平均值。从上图结果看，大多数受试黑猩猩会倾向按下含有两份食物的操作杆（prosoc_left)，而桌子对面是否有另一只黑猩猩对受试黑猩猩影响不大（condition）。不过，上述7个个体的结果变异很大，有4个个体一致性较好，有2个个体“特立独行”，还有1个个体不管哪种实验情景，总是选择按下左侧操作杆（上图最顶部蓝线）。这种个体变异会掩盖我们研究的结果。就受试黑猩猩个体而言，它们自身可能存在用手习惯问题，比如“左撇子”或是“右撇子”。也就是说对于每一个受试个体，其截距可能都是不同的（即两个自变量取值都为0的情况下）。这和混合线性模型的随机截距是一个道理。模型如下：
【注意其中绿框内的截距项变化】
我们将每个受试个体拟合一个随机截距，使用MCMC推测后验概率分布。
d2 <- d
d2$recipient <- NULL
m10.4 <- map2stan(
alist(
pulled_left ~ dbinom(1,p),
logit(p) <- a[actor] + (bp+bpC*condition)*prosoc_left,
a[actor] ~ dnorm(0,10),
bp ~ dnorm(0,10),
bpC ~ dnorm(0,10)
),
data = d2, chains = 2, iter = 2500, warmup = 500
)
precis(m10.4, depth = 2)## Mean StdDev lower 0.89 upper 0.89 n_eff Rhat
## a[1] -0.74 0.27 -1.17 -0.31 2480 1
## a[2] 10.94 5.33 3.87 18.53 1536 1
## a[3] -1.05 0.28 -1.48 -0.60 3244 1
## a[4] -1.05 0.28 -1.48 -0.59 3193 1
## a[5] -0.74 0.27 -1.17 -0.28 2819 1
## a[6] 0.21 0.26 -0.21 0.63 3667 1
## a[7] 1.82 0.40 1.17 2.42 3026 1
## bp 0.84 0.27 0.41 1.28 1969 1
## bpC -0.13 0.31 -0.59 0.40 2751 1这时，每一个受试个体都有一个单独的截距,其中二号个体a[2]的截距是一个很大的正值，也就是说该个体在其他自变量都取值为0时，其更习惯于使用左手，就可能是一个“左撇子”。
上面分析的数据形式是把每一个个体的每一次具体试验都详细列了出来。下面分析的数据形式是汇总的数据。
data("chimpanzees")
d <- chimpanzees
d.aggregated <- aggregate(d$pulled_left,
list(prosoc_left = d$prosoc_left, condition = d$condition, actor=d$actor),
sum)
head(d.aggregated)## prosoc_left condition actor x
## 1 0 0 1 6
## 2 1 0 1 9
## 3 0 1 1 5
## 4 1 1 1 10
## 5 0 0 2 18
## 6 1 0 2 18其中x是每次试验发生的次数。比如上表第二行表示当prosoc_left为0，condition为1时，第一个受试黑猩猩进行了18次实验【本实验设计中每个实验条件组合重复18次】，其中按下左侧操作杆的结果发生了9次。在R中对上述数据进行模型拟合。
m10.5 <- map(
alist(
x ~ dbinom(18,p),
logit(p) <- a + (bp + bpC*condition)*prosoc_left,
a ~ dnorm(0,10),
bp ~ dnorm(0,10),
bpC ~ dnorm(0,10)
),
data = d.aggregated
)如果每次试验的重复次数不是固定的怎么办？比如，上述实验中每个受试黑猩猩的每个实验组合可能测定了10次，20次或者28次。
下面以入学率的例子来说明这种情况。
library(rethinking)
data("UCBadmit")
d <- UCBadmit
print(d)## dept applicant.gender admit reject applications
## 1 A male 512 313 825
## 2 A female 89 19 108
## 3 B male 353 207 560
## 4 B female 17 8 25
## 5 C male 120 205 325
## 6 C female 202 391 593
## 7 D male 138 279 417
## 8 D female 131 244 375
## 9 E male 53 138 191
## 10 E female 94 299 393
## 11 F male 22 351 373
## 12 F female 24 317 341上述数据表示每个学院dept申请者的人数applications，性别applicant.gender，以及最后学院接受申请admit和拒绝申请reject的人数。这是二项分布数据的汇总形式，对于每一个申请者，都可以写成0/1的单独数据形式。
我们通过这个数据想看一看学校入学情况存不存在性别偏倚。为此，我们有下面两个模型：
1）拟合入学人数admit和申请者性别的二项回归模型，判断接受入学概率和性别之间的关系；
2）以admit作为常量拟合二项回归模型，以此判断第一个模型是否存在过度拟合现象。
对于第一个模型：
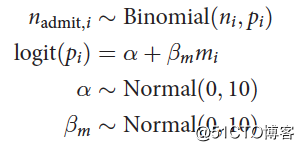
其中下表i表示数据行，表示性别哑变量“男性”。
在R中拟合上述两个模型，并进行比较如下：
d$male <- ifelse(d$applicant.gender == "male",1,0)
m10.6 <- map(
alist(
admit ~ dbinom(applications,p),
logit(p) <- a + bm*male,
a ~ dnorm(0,10),
bm ~ dnorm(0,10)
),
data = d
)
m10.7 <- map(
alist(
admit ~ dbinom(applications,p),
logit(p) <- a,
a ~ dnorm(0,10)
),
data = d
)
compare(m10.6, m10.7)## WAIC pWAIC dWAIC weight SE dSE
## m10.6 5954.9 2 0.0 1 34.98 NA
## m10.7 6046.3 1 91.4 0 29.87 19.18通过上述比较可以看出，包含性别因素的模型的WAIC要比不包含性别因素模型小很多，也就意味着性别是影响接受入学申请的重要因素。
precis(m10.6)## Mean StdDev 5.5% 94.5%
## a -0.83 0.05 -0.91 -0.75
## bm 0.61 0.06 0.51 0.71性别的参数bm是个正数，说明入学偏向于男性。具体来说，男性入学的风险比是女性入学的风险比的exp(0.16)=1.84倍。当然，风险比是一个相对效应，我们前面提到过。如果要描述性别因素的绝对相应，可以如下：
post <- extract.samples(m10.6)
p.admit.male <- logistic(post$a + post$bm)
p.admit.female <- logistic(post$a)
diff.admit <- p.admit.male - p.admit.female
quantile(diff.admit, c(0.025,0.5,0.975))## 2.5% 50% 97.5%
## 0.1132837 0.1415623 0.1692531也就是意味着，男性有14%的可能比女性获得入学机会。结果真的是这样吗？我们通过画图来看。
postcheck(m10.6, n = 1e4)
for(i in 1:6)
{
x <- 1 + 2*(i-1)
y1 <- d$admit[x]/d$applications[x]
y2 <- d$admit[x+1]/d$applications[x+1]
lines(c(x,x+1), c(y1,y2), col=rangi2, lwd=2)
text(x+0.5,(y1+y2)/2 + 0.05, d$dept[x], cex=0.8,col=rangi2)
}
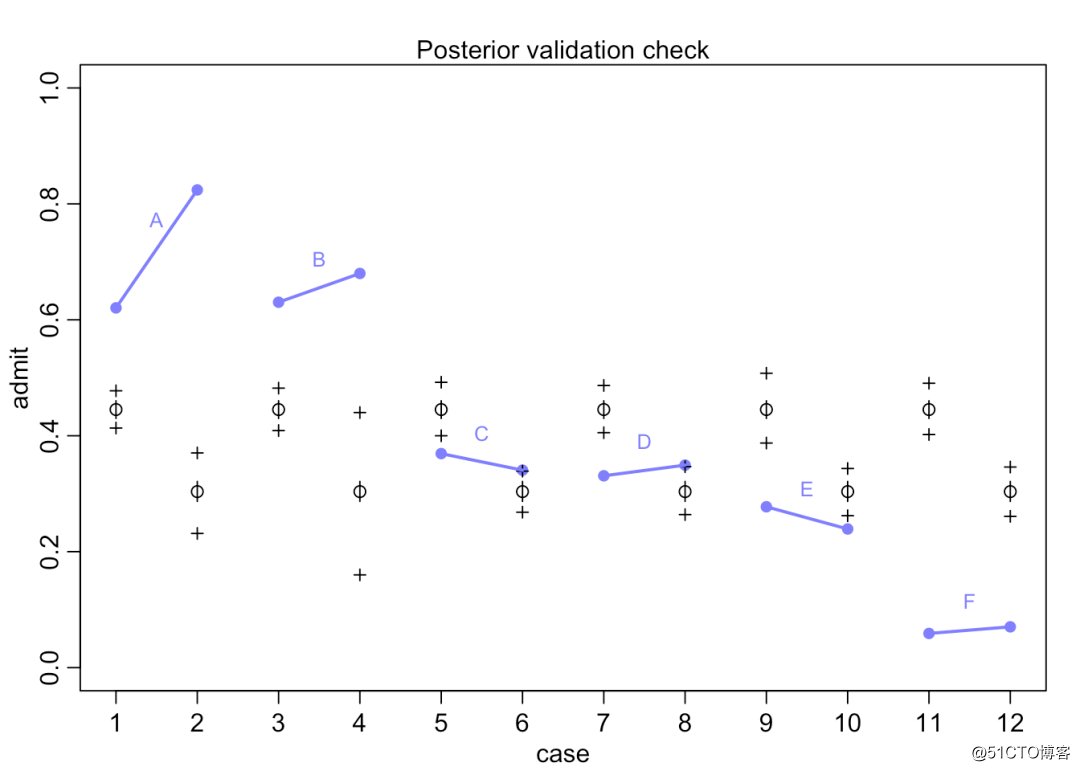
【x轴表示数据集中的12行数据，蓝线表示ABCDEF六个学院实际观测男性-女性的入学率,线段左端为男性，右端为女性。空心点和十字号表示预测的入学率】
从上面的图上看，我们模型的预测结果和实际情况有很大偏差！我们预测的男性入学率高于女性，但是实际只有CE这两个学院的男性入学率高于女性，其他4个学院的男性入学率均低于女性。那么问题出在哪儿呢？！！
我们看一下具体数据可以发现，在总申请人数中，申请AB学院的男性人数远比女性多，而申请EF的男性人数和女性人数相差不大，甚至女性会多于男性。通过上面的图可以看出，AB学院的申请通过率要远比EF学院的通过率高。也就是，更多的女性会喜欢申请通过率低的学院。这也就造成了男性入学的机会比女性更大。而这种差异并不是性别因素本身造成的。所以上面我们拟合的模型实际上是“各个学院整体平均”情况的男女入学率的差异，这给我们造成了很大的误导！
考虑到各个学院的申请通过率本身存在很大差异，为了比较性别因素，我们还应该将各个学院单独考虑，也就是说上述模型我们要加一个随机截距项，而不是一个固定截距项。
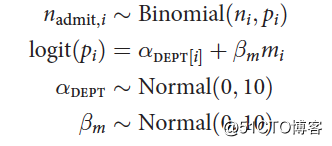
我们将每一个学院设定为单独的一个截距。此时重新拟合不含有性别因素的模型和含有性别因素的模型：
d$dept_id <- coerce_index(d$dept)
m10.8 <- map(
alist(
admit ~ dbinom(applications,p),
logit(p) <- a[dept_id],
a[dept_id] ~ dnorm(0,10)
),data = d
)
m10.9 <- map(
alist(
admit ~ dbinom(applications,p),
logit(p) <- a[dept_id] + bm*male,
a[dept_id] ~ dnorm(0,10),
bm ~ dnorm(0,10)
),data = d
)
compare(m10.6,m10.7,m10.8,m10.9)## WAIC pWAIC dWAIC weight SE dSE
## m10.9 5201.4 6.9 0.0 0.51 56.97 NA
## m10.8 5201.4 6.2 0.1 0.49 56.96 2.52
## m10.6 5954.8 1.9 753.4 0.00 34.94 49.31
## m10.7 6046.4 1.0 845.1 0.00 29.91 52.36比较所有4个模型，m10.8和m10.9比之前的两个模型要好很多，也就是把截距设为随机项，模型拟合更好。不过模型m10.8和m10.9差别不大。详细看一下m10.9模型的参数：
precis(m10.9, depth=2)## Mean StdDev 5.5% 94.5%
## a[1] 0.68 0.10 0.52 0.84
## a[2] 0.64 0.12 0.45 0.82
## a[3] -0.58 0.07 -0.70 -0.46
## a[4] -0.61 0.09 -0.75 -0.48
## a[5] -1.06 0.10 -1.22 -0.90
## a[6] -2.62 0.16 -2.88 -2.37
## bm -0.10 0.08 -0.23 0.03其中，性别bm的参数值变为了-0.1，所以针对学院内男女入学率的比较发现，男性入学的风险比是女性的exp(-0.1) = 0.9【入学概率为0.475】。这和我们之前得到的结论完全相反。之前认为的女性入学率低只是因为她们申请了难度较大的学院，并不是因为她们是女性的原因。所以当我们研究两个变量之间的关系时，如果我们加入第三个变量则可能完全逆转前两者的关系。最著名的例子就是辛普森悖论。对于我们的模型和最后得到的结论不要100%相信，要保持怀疑的态度。
在glm()是R语言的标准函数，对于汇总形式的二分类数据，glm()使用cbind来描述结果变量。比如之前的几个使用rethinking::map函数模型，如果使用glm()函数可以写成下列形式：
m10.7glm <- glm(cbind(admit, reject)~1, data = d, family = binomial)
m10.6glm <- glm(cbind(admit, reject)~male, data = d, family = binominal)
m10.8glm <- glm(cbind(admit, reject)~dept, data = d, family = binomial)
m10.9glm <- glm(cbind(admit, reject)~ male + dept, data = d, family = binomial)对于非汇总形式的二分类数据，同样可以使用glm(),
m10.4glm <- glm(pulled_left ~ as.factor(actor) + prosoc_left*condition - condition,
data = chimpanzees, family = binomial)二项分布的期望值是np，方差是np(1-p)，当n非常大，p非常的小的时候，该二项分布的期望值和方差近乎相等。比如，如果试验次数n=1e5，每次试验的样本量为1000，预期结果发生概率p=1e-3，此时期望值和方差为：
y <- rbinom(1e5,1000,1e-3)
c(mean(y),var(y))## [1] 0.997120 1.004282可以看到，期望平均值和方差大小几乎相等。这时的二项分布也称之为Poisson分布。Poisson分布只有一个参数，来描述分布形状，也表示单位时间段或空间内事件平均发生次数。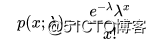
Poisson分布的线性模型可以简化如下表示：
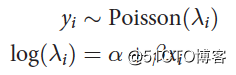
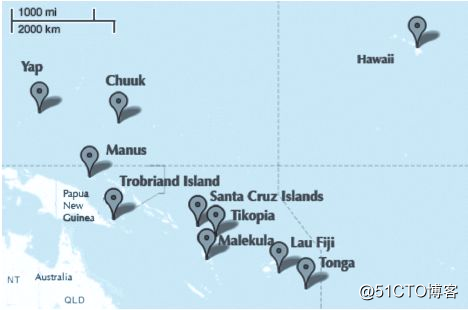
在太平洋一些岛国上有很多原著民，他们的人口数量大小不一，使用的生产工具的数量也有很大不同，比如鱼钩、斧头、船、犁等。有研究理论认为，一个岛上的人口数量越多，该群体使用的工具种类数越多。还有研究提出，岛之间的接触交流程度越高，使用的工具种类数越多。下面是相关研究的一些数据。
library(rethinking)
data("Kline")
d <- Kline
print(d)## culture population contact total_tools mean_TU
## 1 Malekula 1100 low 13 3.2
## 2 Tikopia 1500 low 22 4.7
## 3 Santa Cruz 3600 low 24 4.0
## 4 Yap 4791 high 43 5.0
## 5 Lau Fiji 7400 high 33 5.0
## 6 Trobriand 8000 high 19 4.0
## 7 Chuuk 9200 high 40 3.8
## 8 Manus 13000 low 28 6.6
## 9 Tonga 17500 high 55 5.4
## 10 Hawaii 275000 low 71 6.6第一列是各个岛上的原住民,一共10个群体；第二列是每个群体人口数量；第三列表示群体与其他群体接触交流程度高低；第四列表示使用工具的数量；第五列是其他。
我们建立如下Poisson模型。
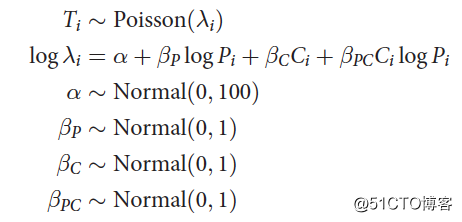
注意，上述模型中，P是人口数，取了对数；C表示交流率高低；同时模型中还加入了P和C的交互项，人口数量和交流率可能存在相关关系。
d$log_pop <- log(d$population)
d$contact_high <- ifelse(d$contact=="high",1,0)
m10.10 <- map(
alist(
total_tools ~ dpois(lambda),
log(lambda) <- a + bp*log_pop + bc*contact_high + bpc*contact_high*log_pop,
a ~ dnorm(0,100),
c(bp,bc,bpc) ~ dnorm(0,1)
),
data = d
)
precis(m10.10, corr = TRUE)
plot(precis(m10.10))## Mean StdDev 5.5% 94.5% a bp bc bpc
## a 0.94 0.36 0.37 1.52 1.00 -0.98 -0.13 0.07
## bp 0.26 0.03 0.21 0.32 -0.98 1.00 0.12 -0.08
## bc -0.09 0.84 -1.43 1.25 -0.13 0.12 1.00 -0.99
## bpc 0.04 0.09 -0.10 0.19 0.07 -0.08 -0.99 1.00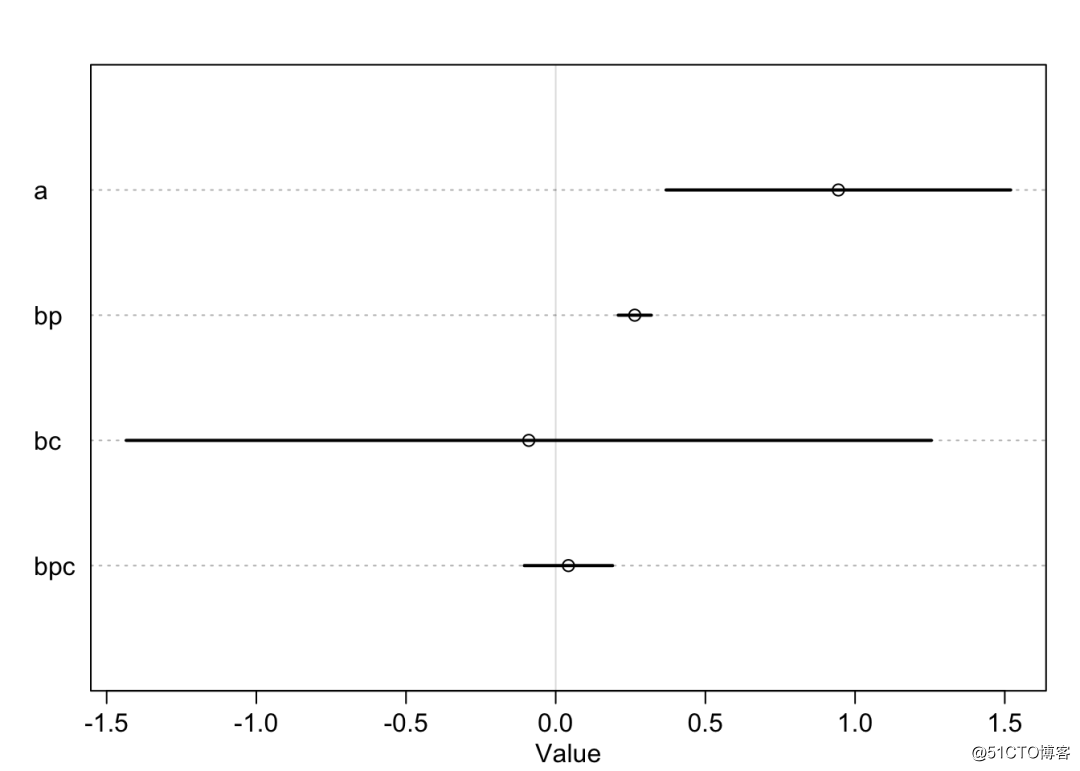
从上面的结果可以看出，对数人口数bp的参数区间不包括0，而bc和bpc的参数区间包括0，所以可以认为使用工具的数量和人口数量有关系，而和交流率没有关系。
不过，上面的结论存在很大问题！真的和交流率没有关系吗？
假设现在有两个对数人口数为8的岛，一个岛是高交流率，另一个岛是低交流率。我们以此来估计他们使用工具数量的后验概率分布，然后比较工具使用数量的差异diff。
post <- extract.samples(m10.10)
lambda_high <- exp(post$a + post$bc + (post$bp + post$bpc)*8)
lambda_low <- exp(post$a + post$bp*8)
diff <- lambda_high - lambda_low
sum(diff>0)/length(diff)## [1] 0.9525结果如下图（左）：
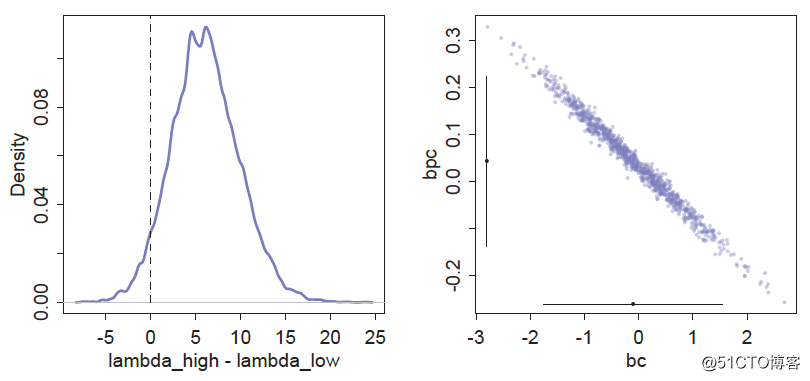
高交流率岛上居民使用的工具数量有95%的可能性比低交流率岛上居民使用工具数量要多。所以交流率也应该是影响工具数量的因素。那么为什么和我们模型的结论不一致呢？
上图（右）表示bp和bpc的相关性。它俩存在明显的负相关。即在交流率低的岛上，交流率和人口数量存在正相关性，反之在交流率高的岛上，交流率和人口数量存在负相关性。所以，我们不能只看单独一个变量的偏不确定性marginal，而应该把所以变量都考虑在内，看多个变量的联合不确定性joint。
一个比较好的做法是使用多个不同的模型，然后进行模型比较。模型的比较是建立在结果变量尺度上的，它包含了各个变量的相关性。同时模型比较也能够帮助识别过度拟合问题。下面是两个自变量，其他不同组合形式的3种模型。
# 包含两个变量，不包含交互作用
m10.11 <- map(
alist(
total_tools ~ dpois(lambda),
log(lambda) <- a + bp*log_pop + bc*contact_high,
a ~ dnorm(0,100),
c(bp,bc) ~ dnorm(0,1)
),
data = d
)
# 只包含人口数量
m10.12 <- map(
alist(
total_tools ~ dpois(lambda),
log(lambda) <- a + bp*log_pop,
a ~ dnorm(0,100),
bp ~ dnorm(0,1)
),
data = d
)
# 只包含接触率高低
m10.13 <- map(
alist(
total_tools ~ dpois(lambda),
log(lambda) <- a + bc*contact_high,
a ~ dnorm(0,100),
bc ~ dnorm(0,1)
),
data = d
)
# 只包含截距项
m10.14 <- map(
alist(
total_tools ~ dpois(lambda),
log(lambda) <- a,
a ~ dnorm(0,100)
),
data = d
)
#比较所有4种模型
islands.compare <- compare(m10.10,m10.11,m10.12,m10.13,m10.14,n=1e4)
plot(islands.compare)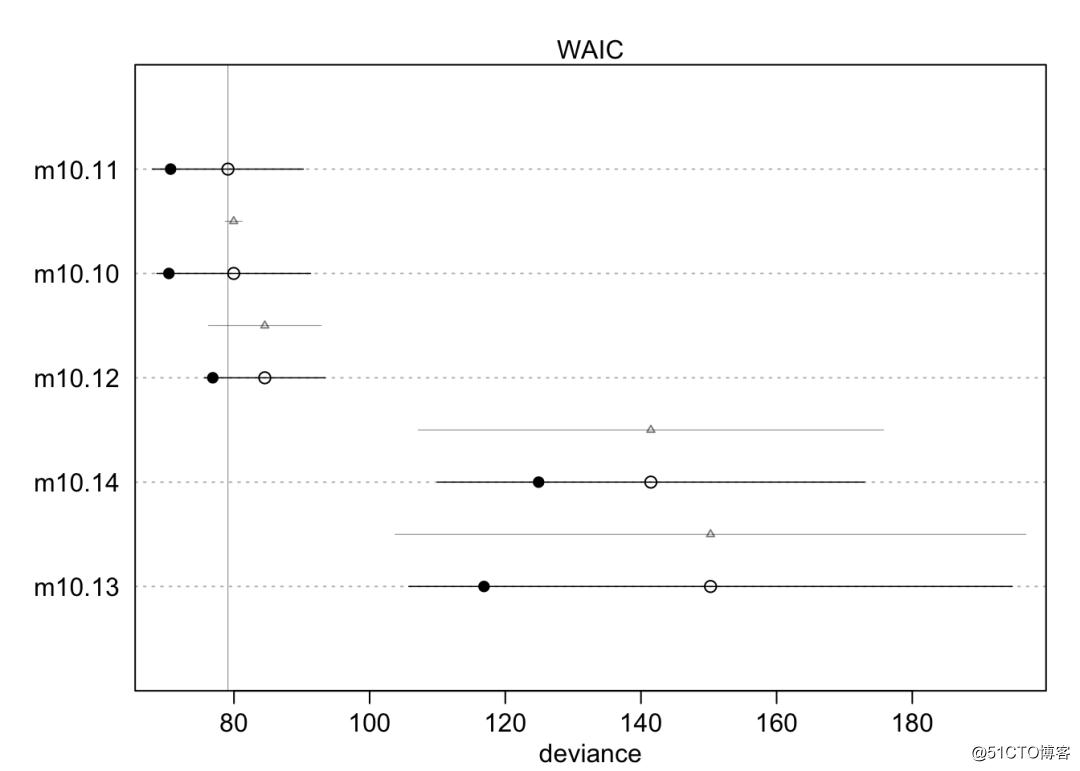
根绝上图可以看到，前3个模型的预测效果都不错，不过模型预测最好的还是m10.11，也就是包含两个自变量，但是不包括交互作用，所以交互项可能是过度拟合。
为了更直观的了解两个自变量和工具数量的关系，综合上述前3个最好的模型，我们通过如下代码作图：
pch <- ifelse(d$contact_high==1,16,1)
plot(d$log_pop, d$total_tools, col = rangi2,pch=pch,
xlab = "log-population",ylab = "total tools")
log_pop.seq <- seq(6,13, length.out = 30)
d.pred <- data.frame(log_pop = log_pop.seq, contact_high = 1)
lambda.pred.h <- ensemble(m10.10,m10.11,m10.12, data = d.pred)
lambda.med <- apply(lambda.pred.h$link, 2, median)
lambda.PI <- apply(lambda.pred.h$link,2,PI)
lines(log_pop.seq, lambda.med, col=rangi2)
shade(lambda.PI, log_pop.seq, col=col.alpha(rangi2,0.2))
# plot low
d.pred <- data.frame(log_pop = log_pop.seq, contact_high = 0)
lambda.pred.l <- ensemble(m10.10,m10.11,m10.12, data = d.pred)
lambda.med <- apply(lambda.pred.l$link, 2, median)
lambda.PI <- apply(lambda.pred.l$link,2,PI)
lines(log_pop.seq, lambda.med, lty=2)
shade(lambda.PI, log_pop.seq, col=col.alpha("black",0.1))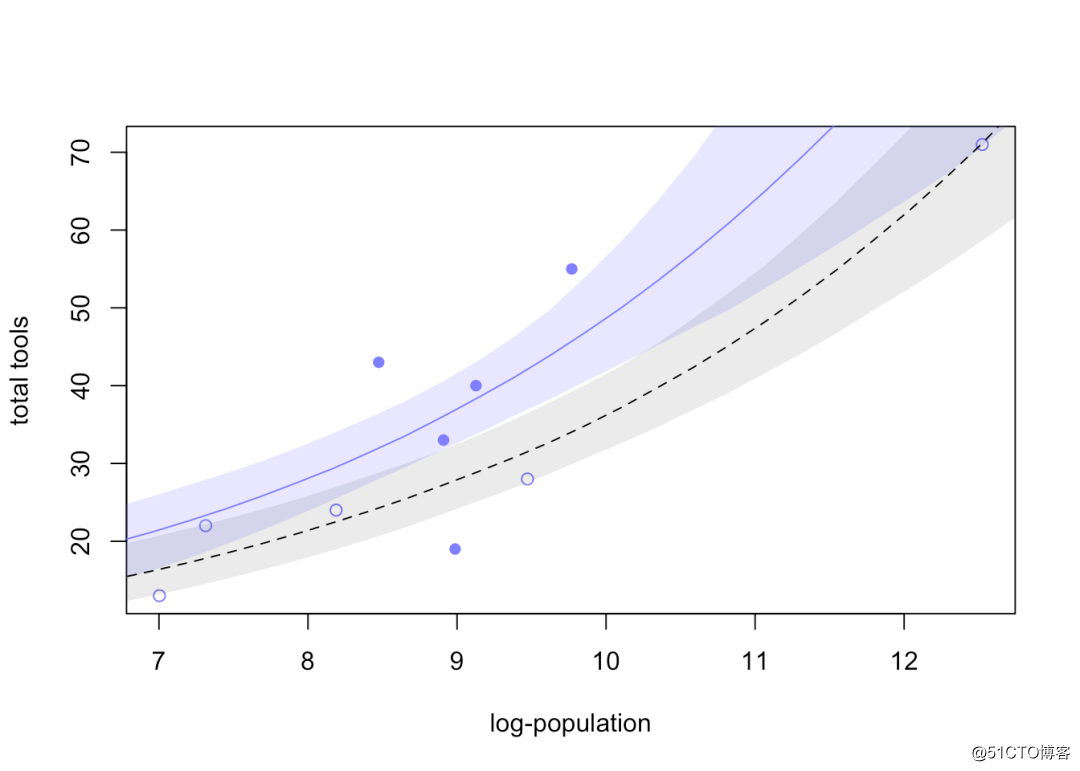
【蓝色部分表示高交流率岛屿，灰色部分表示低交流率岛屿】
通过上图可以很直观的看出，不管是高交流率岛屿还是低交流率岛屿，人口数量的增加都显著的增加了使用工具数量；而高交流率岛屿在中间部分的使用工具数量也显著高于低交流率岛屿。
本文主要介绍了分类计数资料的线性回归模型，包括二项回归模型和Poisson回归模型。通过黑猩猩试验的例子、不同学院男女入学人数和太平洋岛屿原住民使用工具种类数量的例子，分别对上述两个模型进行了剖析。对于分类计数资料我们千万不要将其转化为百分比或者率来分析，这样就损失了样本量信息！
分类计数资料有两种数据形式，一种是logistic数据形式（非汇总形式），另一种是汇总形式。两种数据形式是等价的，不会影响我们最终的分析结果。同时，要注意在数据分析中各个自变量存在的相关性可能会干扰结果，掩盖真实的效应，在数据分析过程中务必对自变量之间的相关性进行核查，同时，通过图形形式来展示模型拟合和预测结果对我们的理解和解释很有帮助。此外，要注意模型参数的相对效应和绝对效应。对数风险比很大，不一定意味着带来的实际效应会很大，还要结合具体模型，将参数转化为原始数据形式进行解释。
当然，除了上述两种常见的分类计数资料的线性回归模型，还有其他几种模型，比如多分类资料回归模型、几何分布模型、负二项回归模型和beta-二项分布模型等。
【THE END】
资料来源：《statistical rethinking》
标签：library ant data 转化 port mil 理论 reject 单位
原文地址：https://blog.51cto.com/15069450/2577075
