标签:就是 odi 表示 查看 rds open 联系 Once mes
好久没写博客了
这次准备在 cnblogs 和 我的博客 上同步更新~
一个 \(n\) 个点 \(m\) 条边的 DAG,有若干个特殊点,边有权值。
一个单词定义为从点 \(1\) 出发到达一个特殊点的路径上,边权按访问顺序构成的一个序列。
\(Q\) 次询问,每次给出 \(k\),求所有单词中字典序从小到大第 \(k\) 个单词的长度,或回答“不存在”。
\(2\le n\le10^5\),\(0\le m\le10^5\),\(1\le k\le10^8\);保证 \(1\) 不是特殊点且 \(1\) 没有入度;保证一个点的所有出边的权值两两不同。
思路挺让人震惊的……原来不仅树可以剖分
可惜的是,但凡 \(k\) 的范围开大到 \(10^9\) 就放不过那种直接跑出 \(10^8\) 的答案的暴力 awa
首先不难想到DP,先求出 \(f_u\) 表示从 \(u\) 出发能够得到多少个单词。转移式很简单,
不过考虑到单词数会非常大,远远大于 \(10^8\),会爆 int,所以当 \(f_u>2\times10^8\) 时就把 \(f_u\) 赋值为 \(2\times10^8\)(不和 \(10^8\) 取 min,还是留一点超出的空间)。
然后先想暴力,每次询问从 \(1\) 出发,按权值从小到大查看出边,如果构成的单词数量足够 \(k\),就从那条出边递归到子问题。复杂度是 \(O(Qn)\) 的。
具体看一下怎么递归子问题,设点 \(u\) 的出边按权值从大到小为 \(w_1,w_2,\dots,w_t\),如果我们发现:
说明应从边 \(i\) 转移,于是递归子问题 k-=w[1]+w[2]+...+w[i-1]。
注意到每次 \(k\) 都会减小一些,于是就有了一个很妙的想法——对于一个点 \(u\),定义其重儿子为 dp 值最大的一个出点,其他出点就是轻儿子。
实际上直接这样定义,理论复杂度会有小问题(但是实测可过),理论复杂度正确的定义应是“dp 值小于 \(2\times10^8\) 的 dp 值最大的出点”
也就是说忽略 dp 值太大的点,以下均假设 \(f_u\le10^8\)。
这样有什么性质?设 \(u\) 的重儿子是 \(p\),一个轻儿子是 \(q\),则 \(f_p\ge f_q\)。如果我们要转移到 \(q\),转移后的子问题为 \(k‘\),则 \(k‘\le f_q\le \frac{f_p+f_q}2\le\tfrac12f_u\)。
这样的话,\(k\) 的上界每次减半,只能减 \(O(\log f)\) 次,于是只会经过 \(O(\log f)\) 次轻边。
两者都是利用的这种“上界减半”的思想。
树链剖分中如果走轻儿子,则子树大小一定减半,那么只会走 $O(\log n)$ 次轻儿子,也就是“一条链只会被剖成 $O(\log n)$ 条重链”这一结论。而走重儿子这种情况,重儿子构成重链,链是一种更简单的结构,因此可以用一些处理序列的数据结构维护。
而这道题将 DAG 剖成“重链”——实际上不是链,而是一棵树,同样简化了图结构。接下来就可以用一些树的技巧解题了。
那如果从重儿子转移呢?这一就不一定满足“上界减半”。但是不难发现重儿子构成了内向树森林 的结构,能不能用什么树的技巧来加速走重儿子的过程?
考虑倍增,维护 \(u\) 的第 \(2^i\) 级祖先 jump[u][i],以及从 \(\mathbf u\) 转移到该祖先之间有多少个字符串 jumpcst[u][i]。画个图可能会好理解一些:
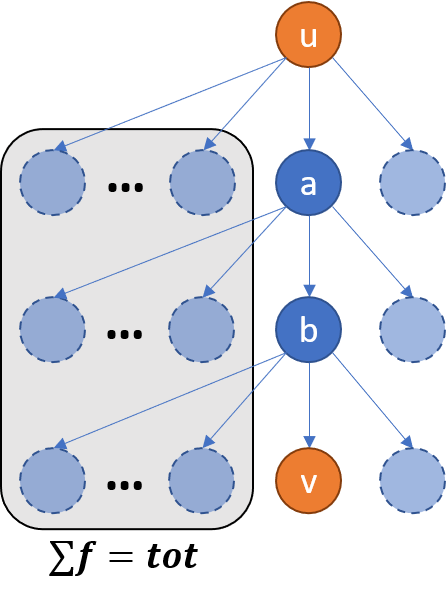
(\(tag_u=1\) 表示 \(u\) 是特殊点)比如从 \(u\) 到 \(a\),\(a\) 左边的所有儿子代表的单词都会被跳过,而且如果 \(u\) 本身是特殊点,在 \(u\) 结尾的单词也会被跳过。
那么可以从 \(u\) 直接倍增到 jump[u][i] 的条件就是
别忘了还有上界。
显然可以倍增,复杂度 \(O(\log n)\)。而走轻儿子就可以直接二分,预处理每个点的出边权值从小到大的 dp 值前缀和即可。
总的复杂度,每次查询会走 \(O(\log f)\) 次轻儿子,每次 \(O(\log n)\) 二分;会走 \(O(\log f)\) 次重链,每次 \(O(\log n)\) 倍增,总的复杂度加上预处理为 \(O(Q\log n\log f+n\log n)\)。
/*Lucky_Glass*/
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
inline int Rint(int &r){
int b=1,c=getchar();r=0;
while(c<‘0‘ || ‘9‘<c) b=c==‘-‘? -1:b,c=getchar();
while(‘0‘<=c && c<=‘9‘) r=(r<<1)+(r<<3)+(c^‘0‘),c=getchar();
return r*=b;
}
const int N=1e5+10;
#define ci const int &
typedef pair<int,int> pii;
int n,m,Q,cas;
int sptag[N],dp[N],son[N],dpcst[N],jump[N][20],jumpcst[N][20];
bool dpdone[N];
vector<pii> lnk[N];
vector<int> key[N];
//dpcst[u]: 从u到son[u]需要跳过多少字符串
//key[u][i]: 从u到lnk[u][i]需要跳过多少字符串
int DP(ci u){
if(dpdone[u]) return dp[u];
dpdone[u]=true,dpcst[u]=dp[u]=sptag[u];
for(int it=0,iit=lnk[u].size();it<iit;it++){
int v=lnk[u][it].second;
DP(v);
//实际上不加 dp[u]<=1e8 也能过……
if(dp[son[u]]<dp[v] && dp[u]<=1e8) son[u]=v,dpcst[u]=dp[u];
dp[u]+=dp[v];
if(dp[u]>2e8) dp[u]=2e8;
key[u].push_back(dp[u]);
}
jump[u][0]=son[u],jumpcst[u][0]=dpcst[u];
for(int i=1;i<20;i++){
jump[u][i]=jump[jump[u][i-1]][i-1];
jumpcst[u][i]=jumpcst[u][i-1]+jumpcst[jump[u][i-1]][i-1];
if(jumpcst[u][i]>2e8) jumpcst[u][i]=2e8;
}
return dp[u];
}
int Jump(int rnk){
int u=1,ret=0;
while(true){
if(rnk>dp[u]) exit(0);
for(int i=19;~i;i--)
if(jump[u][i] && rnk>jumpcst[u][i]){
int v=jump[u][i];
if(rnk>jumpcst[u][i]+dp[v]) continue;
rnk-=jumpcst[u][i];
u=v,ret+=(1<<i);
}
if(rnk==1 && sptag[u]) return ret;
int tmp=int(lower_bound(key[u].begin(),key[u].end(),rnk)-key[u].begin());
if(tmp) rnk-=key[u][tmp-1];
else rnk-=sptag[u];
u=lnk[u][tmp].second,ret++;
}
}
void Solve(){
Rint(n),Rint(m),Rint(Q);
for(int i=1;i<=n;i++){
if(i>1) Rint(sptag[i]);
dpdone[i]=false;
lnk[i].clear(),key[i].clear();
son[i]=dpcst[i]=0;
for(int j=0;j<20;j++) jump[i][j]=jumpcst[i][j]=0;
}
for(int i=1,u,v,varc;i<=m;i++){
Rint(u),Rint(v),Rint(varc);
lnk[u].push_back(make_pair(varc,v));
}
for(int i=1;i<=n;i++) sort(lnk[i].begin(),lnk[i].end());
DP(1);
while(Q--){
int rnk;Rint(rnk);
if(rnk>dp[1]) printf("-1\n");
else printf("%d\n",Jump(rnk));
}
}
int main(){
// freopen("input.in","r",stdin);
Rint(cas);
for(int i=1;i<=cas;i++){
printf("Case #%d:\n",i);
Solve();
}
return 0;
}
> Linked 今日重到苏澜桥-网易云
OI - GRE Words Once More!(HDU)
标签:就是 odi 表示 查看 rds open 联系 Once mes
原文地址:https://www.cnblogs.com/LuckyGlass-blog/p/14244225.html