标签:while 技术 ctc 节点 || lazy out bsp 头结点
题目:
思路:
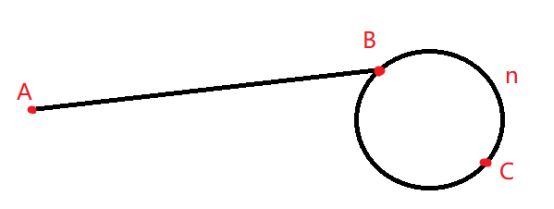
首先画个图出来,假设有两个指针指向头结点-----p1与p2,那么当p1走一步,而p2走两步,如果存在圆,那么必然会出现,p1与p2同时落在C处(即重合点)。故此时链表有环。
其次,题目要求我们取出入口节点,由上可知,
假设
链表头到环入口AB长度为——a,
环入口到相遇点BC长度为——b,
相遇点到环入口CB长度为——c
则相遇时,
快指针路程=a+(b+c)k+b,k>=1,其中b+c为环的长度,k为环的圈数(k>=1,即最少一圈,不能是0圈,不然快慢指针走的路程一样,矛盾)。
慢指针路程=a+b。
因为快指针的路程是慢指针的路程的两倍,所以:(a+b)*2=a+(b+c)k+b。
化简得:
a=(k-1)(b+c)+c,这个式子的意思是:链表头到环入口的距离=相遇点到环入口的距离+(k-1)圈数环长度。其中k>=1,所以k-1>=0圈。所以两个指针分别从链表头和相遇点出发,最后一定相遇于环入口。
代码示例:
public class Solution4 {
public static void main(String[] args) {
ListNode head = null;
System.out.println(detectCycle(head));
}
/**
* 分拆开的步骤
*
* @param head
* @return
*/
public static ListNode detectCycle(ListNode head) {
if (head == null || head.next == null)
return null;
//定义指针
ListNode p1 = head;
ListNode p2 = head;
//判断是否有环
while (p2.next != null && p2.next.next != null) {
p1 = p1.next;
p2 = p2.next.next;
if (p1 == p2) {
break;
}
}
//如果没有环,return null
if (p2.next == null || p2.next.next == null) {
return null;
}
//如果有环,两个指针分别从链表头和相遇点出发
p1 = head;
while (p1 != p2) {
p1 = p1.next;
p2 = p2.next;
}
return p1;
}
public static ListNode detectCycle2(ListNode head) {
if (head == null || head.next == null)
return null;
//定义指针
ListNode p1 = head;
ListNode p2 = head;
//判断是否有环
while (p2.next != null && p2.next.next != null) {
p1 = p1.next;
p2 = p2.next.next;
if (p1 == p2) {
//如果有环,两个指针分别从链表头和相遇点出发
p1 = head;
while (p1 != p2) {
p1 = p1.next;
p2 = p2.next;
}
return p1;
}
}
return null;
}
}
class ListNode {
int val;
ListNode next;
ListNode(int x) {
val = x;
next = null;
}
}
链表中环的入口节点
标签:while 技术 ctc 节点 || lazy out bsp 头结点
原文地址:https://www.cnblogs.com/chafry/p/14273766.html