深度优先遍历DFS

标签：node   连通   max   code   dfs   一个   它的   代码   状态   

算法思想

??图中一个未访问的顶点 V 开始，沿着一条路一直走到底，然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到底...，不断递归重复此过程，直到所有的顶点都遍历完成，它的特点是不撞南墙不回头，先走完一条路，再换一条路继续走。

代码实现

1. 邻接矩阵实现：

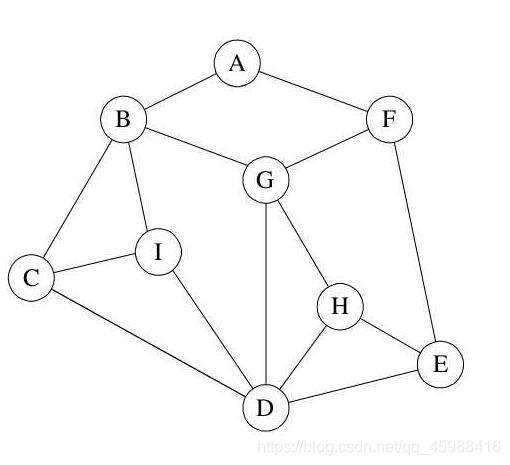
   • 结构体定义：使用二维数组来定义，存入一个结构体中，记录顶点个数。演示是无向图的邻接矩阵

     #define MAX 10
     struct MGraph{
     	int	arr[MAX][MAX];		//存储图的连通状态：1为连通，0为非连通
     	int numVertexes;		//图的顶点数
     };
     int visit[MAX];				//访问标记数组
     

   • DFS算法设计：

     void DFS(MGraph G, int i) {					//i就是顶点的下标
     	visit[i] = true;						//标记访问
     	for (int j = 0;j < G.numVertexes;j++)	//遍历每一个顶点
     		if (G.arr[i][j] && !visit[j])		//如果相连并且没有被访问过
     			DFS(G, j);						//再次调用DFS算法
     }
     

   • 算法入口：

     void DFSTraverse(MGraph G) {
     	memset(visit, 0, G.numVertexes);	//初始化
     	for (int i = 0;i < G.numVertexes;i++)	//对每一个未曾访问过的顶点进行访问
     		if (!visit[i])
     			DFS(G, i);
     }
     

2. 邻接表实现

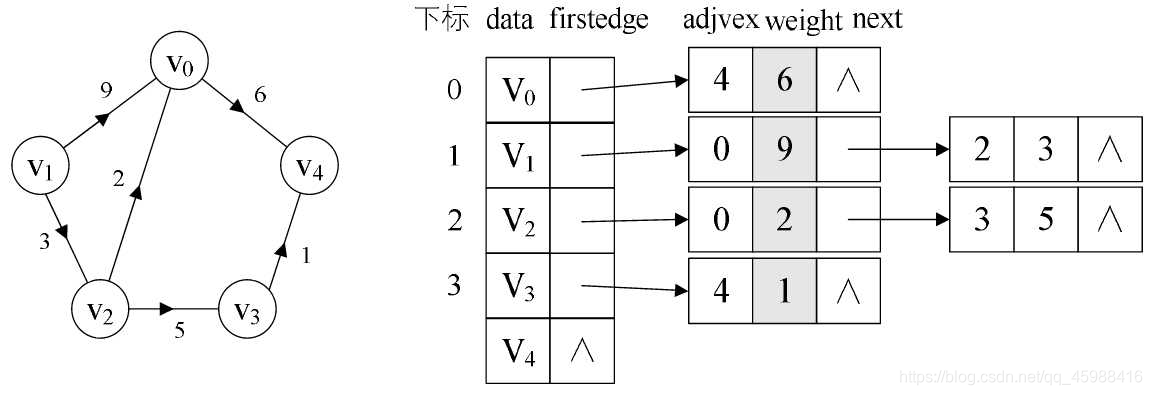
• 结构体定义

  #define MAX 10
  struct EdgeNode {		//存储边的信息
  	int adjvex;			//存储所指向的顶点
  	int weight;			//存储边的权值
  	EdgeNode* next;
  };
  struct VertexNode{
  	int data;			//存储顶点的值
  	EdgeNode* first;	//边
  };
  typedef VertexNode AdjList[MAX];//顶点列表
  struct GraphAdjList{
  	AdjList adjlist;	//列表
  	int numVertexes, numEdges;	//边的数目和顶点的数目
  };
  int visit[MAX];				//访问标记数组
  

• DFS算法设计

  void DFS(GraphAdjList *GL, int i){
  
  	visit[i] = true;
  	EdgeNode* p = GL->adjlist[i].first;
  	while (p) {
  		if (!visit[p->adjvex])DFS(GL, p->adjvex);
  		p = p->next;
  	}
  }
  

• 算法入口

  void DFSTraverse(GraphAdjList *GL){
  	memset(visit, 0, GL->numVertexes);	//初始化
  	for (int i = 0; i < GL->numVertexes; i++)
  		if (!visit[i])
  			DFS(GL, i);
  }
  

深度优先遍历DFS

标签：node   连通   max   code   dfs   一个   它的   代码   状态   

原文地址：https://www.cnblogs.com/3236676588buladuo/p/14394360.html