[POI2006]OKR-Periods of Words 题解

标签：思想   char s   匹配   算法   inf   space   复杂   作者   include   

A 题面

对于一个仅含小写字母的字符串 \(a\) ，若 \(p\) 为 \(a\) 的前缀且 \(p\ne a\) ，那么我们称 \(p\) 为 \(a\) 的 \(proper\) 前缀。

规定字符串 \(Q\)（可以是空串）表示 \(a\) 的周期，当且仅当 \(Q\) 是 \(a\) 的 \(proper\) 前缀且 \(a\) 是 \(Q+Q\) 的前缀。

例如 \(ab\) 是 \(abab\) 的一个周期，因为 \(ab\) 是 \(abab\) 的 \(proper\) 前缀，且 \(abab\) 是 \(ab+ab\) 的前缀。

求给定字符串所有前缀的最大周期长度之和。

输入样例：8 babababa

输出样例：24

B 解题

首先概述一下题意： 对于一个长度为 \(k\) 的字符串 \(A\) 的每个前缀 \(\text{pre}(A, i)\)，求出最长的字符串 \(S_i\) 使得 \(|S_i|<i\) 且 \(A_i\) 是若干个 \(S_i\) 连接在一起的前缀。求出 \(|S_1|+ |S_2| + \cdots + |S_k|\) 。

我们通过样例来看看， 比如我们取 \(\text{A}=\)babababa 的前缀 \(\text{P}\)= bababa，我们将两个字符串 \(\text{A}\) 和 \(\text{P+P}\) 放在一起来比对一下：

P+P:bababa bababa
A:  bababa ba

我们发现 \(\text{A}\) 的后两个字符与 \(\text{PP}\) 的后面的 \(\text{P}\) 前两个的位置相同。这前两个字符其实就是 \(\text{A}\) 的前缀，同时也是 \(\text P\) 的公共前缀后缀。题目要求这个前缀 \(\text P\) 需要是 \(proper\) 前缀，此处可以窥见 KMP 算法的端倪了。

让我们画张图看看（作者不会画图）

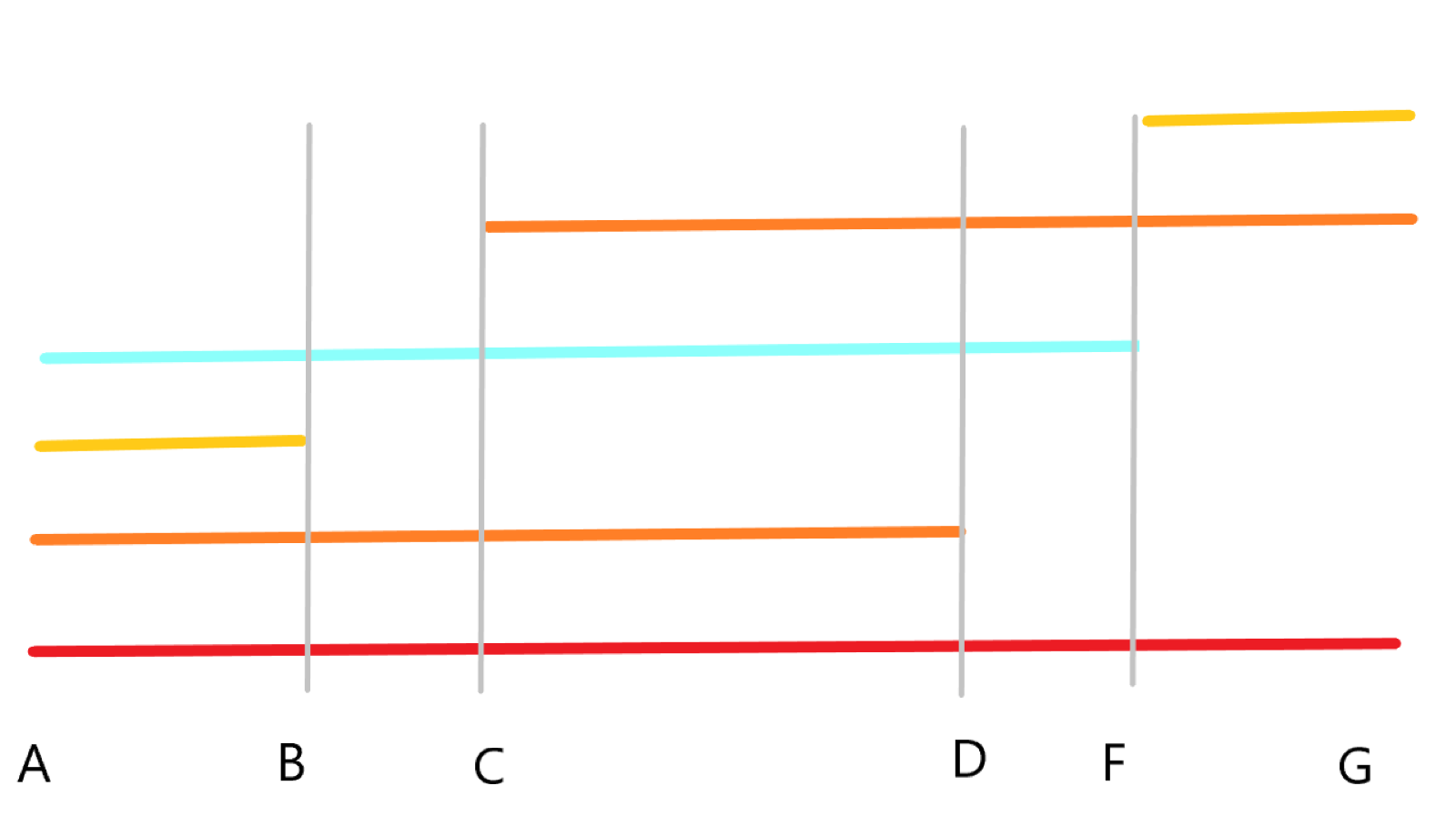
图中，相同颜色线段表示相同字符串

• 线段 \(\text{AG}\)，红色线段是字符串 \(A\)
• 线段 \(\text{AD=CG}\) 橙色线段是 \(A\) 的 \(proper\) 前缀 \(P\)
• 线段 \(\text{AB=FG}\) 棕色线段是 \(P\) 的前后缀

可以发现线段 \(\text{AF}\) ，蓝色线段即使答案之一（一下用加 \(\prime\) 的方式表示 \(\text{AF}\) 复制得到的那一段）

脑补一下，蓝色线段复制一下，\(\text A^{\prime}\text B^{\prime}\) 段和 \(\text{FG}\) 段重合，然后 \(\text B^{\prime} \text F^{\prime}\) 段和 \(\text{AD}\) 段重合。

这不就是 KMP 算法吗？我们把上述的线段用 KMP 的 \(nex\) 数组表示出来（虽然我更喜欢叫他 \(fail\) 数组）

• 线段 \(\text{AD=CG}\) 橙色线段是 \(nex[|\text A|]\)
• 线段 \(\text{AB=FG}\) 棕色线段是 \(nex[|\text P|]\)，也就是 \(nex[next[|\text A|]]\)

题目要求的是什么呢？是想让周期尽可能的大，也就是线段 \(\text{FG}\) 尽可能的短，

所以答案就是 \(|\text A|-\min(\text A的公共前缀后缀)\)

于是最开始，设 \(j=nex[|\text A|]\) ，然后直接暴跳到 $nex[j]=0 $ 的时候就可以了。

但是有一个问题，这样不断地跳，可能会造成时间复杂度退化成 O(n^2)，那我们怎么办？

1. 可以发现我们跳 \(nex\) 的过程很像递归，所以可以借助记忆化的思想， 把刚才求出的最短公共前缀后缀的长度更新到 \(nex\) 数组里头（之前求最长公共前缀后缀的长度的数组），具体见代码。这种方法的时间复杂度依然是 \(O(n)\) 的

2. 第二种想法具体看 这里 ，其主要思想是通过倍增

C 代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;//不开long long见祖宗好吧
const int N = 1000010;

char s[N];
int n,fail[N];//这里的 fail 数组就是 KMP 自匹配的 nex 数组

int main(){
    scanf("%d%s",&n,s+1);
    ll ans=0;fail[1]=0;
    for(int i=2,j=0;i<=n;i++){//KMP 模板
        while(j&&s[i]!=s[j+1])j=fail[j];
        if(s[i]==s[j+1])j++;
        fail[i]=j;
    }
    for(int i=1;i<=n;i++){
        int j=i;
        while(fail[j])j=fail[j];//求最短匹配长度
        if(fail[i])fail[i]=j;//修改 fail 数组，记忆化
        ans+=i-j;//答案显然就是 i-j，统计一下
    }
    printf("%lld",ans);
    return 0;
}

[POI2006]OKR-Periods of Words 题解

标签：思想   char s   匹配   算法   inf   space   复杂   作者   include   

原文地址：https://www.cnblogs.com/wyb-sen/p/14397307.html