标签:问题 文章 独立 难题 image bae weixin mic http
如下图,已知:AB=AC,∠A=∠DCA=20°,∠ABE=30°。求:∠CDE。
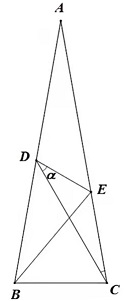
解法一:(walls老师提供)
在AB边上取点F使得FC=BC,连接FC、FE。如下图所示:
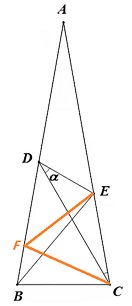
由AB=AC以及∠A=20°,知∠ABC=∠ACB=80°。
由FC=BC知,∠BFC=∠FBC=80°,∠FCB=180°-80°-80°=20°。于是
∠ECF=∠ACB-∠FCB=80°-20°=60°
由∠EBC=∠ABC-∠ABE=80°-30°=50°,以及∠BEC=∠ABE+∠A=30°+20°=50°,知CE=BC=FC。
于是CEF为正三角形。
由∠CDF=∠DCA+∠A==20°+20°=40°,以及∠DCF=∠ECF-∠DCA=60°-20°=40°,知DF=FC=FE。
即有∠FDE=∠FED。而∠DFE=180°-∠BFC-∠CFE=180°-80°-60°=40°,于是
∠FDE=(180°-40°)/2=70°
∠CDE=∠FDE-∠BDC=70°-40°=30°
解法二:由题设知:∠BDC=∠A+∠DCA=40°,CD=AD<AB=AC。
于是在CA上一定有点F,使得CF=CD,连接DF,并延长至点G使得DG=AD,连接AG,如下图所示:
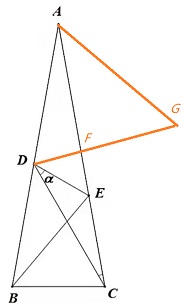
CDF为等腰三角形,且∠DCA=20°,可知∠CDF=80°,∠ADF=180°-∠BDC-∠CDF=60°
于是ADG为正三角形。
考察△BDC和△FAG,易知∠BDC=∠FAG=40°,∠BCD=∠BCA-∠DCA=80°-20°=60°=∠G,再由CD=AD=AG,可知
△BDC和△FAG全等,于是BC=FG。
另外,由∠BEC=∠ABE+∠BAE=30°+20°=50°,∠CBE=∠CBD-∠ABE=80°-30°=50°,可知BC=CE。
于是CE=FG。
由FD=DG-FG,FE=CF-CE,CF=CD=AD=DG,可知FD=FE,于是∠FDE=∠FED。
再由∠DFC=80°,可知∠FDE=(180°-80°)/2=50°。
于是∠CDE=180°-60°-50°-40°=30°。
附言:
最初是在《遇见数学》公众号一篇文章里看到这个题的,里面介绍这个题是著名的几何难题:汤普森问题,我尝试了一阵没做出来。然后看了文章里提供的两个解法之后受到启发才有了上面的解法二。而解法一是walls老师是在完全不知情的情况下独立做出来的,相比解法二以及公众号文章里的两个解法,这个解法显得更加自然,举重若轻。
https://mp.weixin.qq.com/s/LuQb8uCYXgZPcqEevCQw5Q
这是那篇文章的URL。看里面的解法序号可以推测《几何明珠》那本书里至少提供了这题的九种解法。这里的两个解法有可能也在那本书里。
标签:问题 文章 独立 难题 image bae weixin mic http
原文地址:https://www.cnblogs.com/readalps/p/14399787.html