标签：答案   查询   lan   ssi   地方   strong   namespace   lazy   span   

文章中若有不严谨或错误的地方，欢迎在评论中指出QAQ

Description

题目链接

这是一道交互题，题目给出长度为 \(n\) 的数组 \(a\) ，每次查询的格式为 "? \(l\) \(r\)"，其中 \(l\) 和 \(r\) 为查询的区间左端点和右端点，注意 \(l \le r\)。你会得到 [\(l\),\(r\)] 内第二大值所在的位置。

限制查询的次数为最多20次，数组 \(a\) 中的最大值在什么位置，并将其位置以 "! position" 格式输出。

\((2 \leq n \leq 10^5)\) , \((1 \leq l < r \leq n)\)

Solution

首先可以知道，第一次在 1~n 内进行查询，会得到整个 \(a\) 数组的第二大值的位置，这里将其位置记作 \(k\)，然后该位置会将整个区间分为左右两部分。

然后查询左部分，若得到的位置 \(pos\) 与 \(k\) 相同，那么最大值一定在左区间，否则一定在右区间。

这样我们可以对这个区间进行二分，查询二分中点 \(mid\) 与 \(k\) 的值。

若所得到的 \(pos = k\)，那么其答案一定在 \(mid\) ~ \(r\)，否则一定在 \(l\) ~ \(mid\)。

下面以 5 1 4 2 3 为例

第一次查找 1~5 区间，得到位置 \(k=3\)。

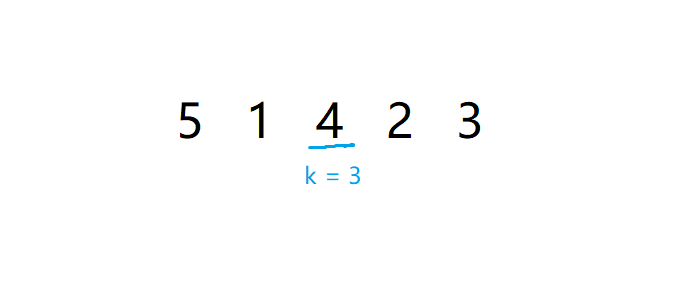
然后查找左区间发现得到的 \(pos=k=3\)。

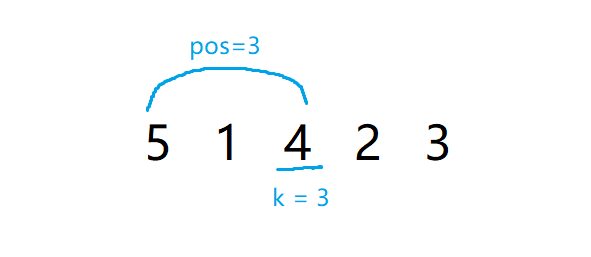
所以答案一定在左区间，这里令 \(l=1,r=k-1\) 然后进行二分，每次询问 \(mid\) ~ \(k\)。

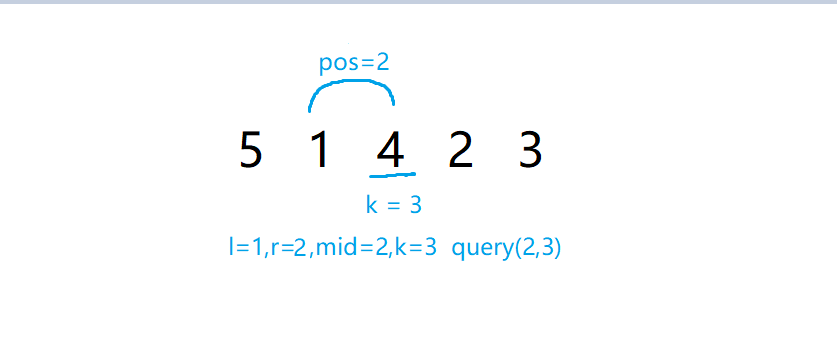
第一次查询发现得到的 \(pos\) != \(k\)，所以答案一定是在 \(mid\) 左边，令 \(r = mid-1\)

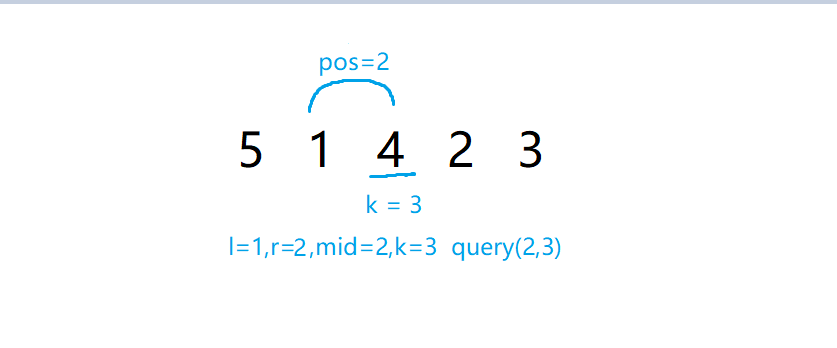
这里发现更新完后 \(l = r\)，那么l就是所要求的答案。

Code

#include <cstdio>

using namespace std;

int ask(int l,int r)
{
    int idx;
    printf("? %d %d\n",l,r);
    fflush(stdout);
    scanf("%d",&idx);
    return idx;
}

void solve(int a,int b)
{
    int left;
    int k = ask(a,b);
    if(a == k) left = 0;
    else left = ask(a,k);
    int ans = 0;
    if(left == k) // 在左边
    {
        int l = a,r = k-1;
        while(l < r)
        {
            int mid = l + r + 1>> 1;
            if(ask(mid,k) == k) l = mid;
            else r = mid - 1;
        }
        ans = l;
    }
    else // 在右边
    {
        int l = k + 1,r = b;
        while(l < r)
        {
            int mid = l + r >> 1;
            if(ask(k,mid) == k) r = mid;
            else l = mid + 1;
        }
        ans = l;
    }
    printf("! %d\n",ans); 
}

int main()
{
    int n;
    scanf("%d",&n);
    solve(1,n);
    return 0;
}

[Codeforces 1486C2]Guessing the Greatest (hard version)

标签：答案   查询   lan   ssi   地方   strong   namespace   lazy   span   

原文地址：https://www.cnblogs.com/Crystar/p/14415408.html