标签:代码实现 enc closed nta fence line pen lazy 常见
二叉排序树的弊端
数列:1,2,3,4,5,6
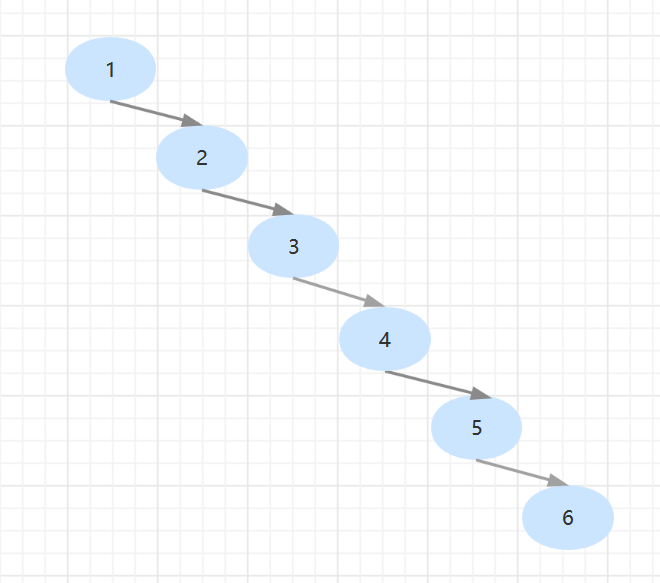
平衡二叉搜索树
AVL树
保证查询效率最高
一颗空树或者是一颗左右两颗子树的高度差的绝对值不超过1, 并且左右子树分别也是平衡二叉树的树

// 树结点 private static class TreeNode{ ? int val; TreeNode left; TreeNode right; ? public TreeNode(int val) { this.val = val; } }

// 返回结点的高度 public int height(){ return Math.max(left == null ? 0 : left.height(), right == null? 0 : right.height()) + 1; } ? // 返回左子树的高度 public int leftHeight(){ if (left == null){ return 0; } return left.height(); } ? // 返回右子树的高度 public int rightHeight(){ if (right == null){ return 0; } return right.height(); }

// 根据二叉排序树的规则添加结点 public void add(TreeNode newNode){ ? if (newNode == null){ return ; } ? /** * 如果当前新结点的值大于当前结点this * 如果当前结点右子树为空,直接添加 * 否则,右子树重新调用add方法,重复此步骤 */ if (newNode.val >= this.val){ if (this.right == null){ this.right = newNode; }else { this.right.add(newNode); } }else { if (this.left == null){ this.left = newNode; }else { this.left.add(newNode); } } }

private static class AVL{ ? // 根节点 private TreeNode root; ? }

// 返回左子树高度 public int leftHeight(TreeNode node){ if (node == null){ return 0; } return node.leftHeight(); } ? // 返回右子树高度 public int rightHeight(TreeNode node) { if (node == null) { return 0; } return node.rightHeight(); } ? // 返回树的高度 public int height(TreeNode node){ if (node == null) { return 0; } return node.height(); }

// 返回左子树高度 public int leftHeight(TreeNode node){ if (node == null){ return 0; } return node.leftHeight(); } ? // 返回右子树高度 public int rightHeight(TreeNode node) { if (node == null) { return 0; } return node.rightHeight(); } ? // 返回树的高度 public int height(TreeNode node){ if (node == null) { return 0; } return node.height(); }

// 添加结点 public void add(TreeNode node){ // root为空,说明node为构建树的第一个结点 if (root == null){ root = node; }else { root.add(node); } }
数列4,3,6,5,7,8
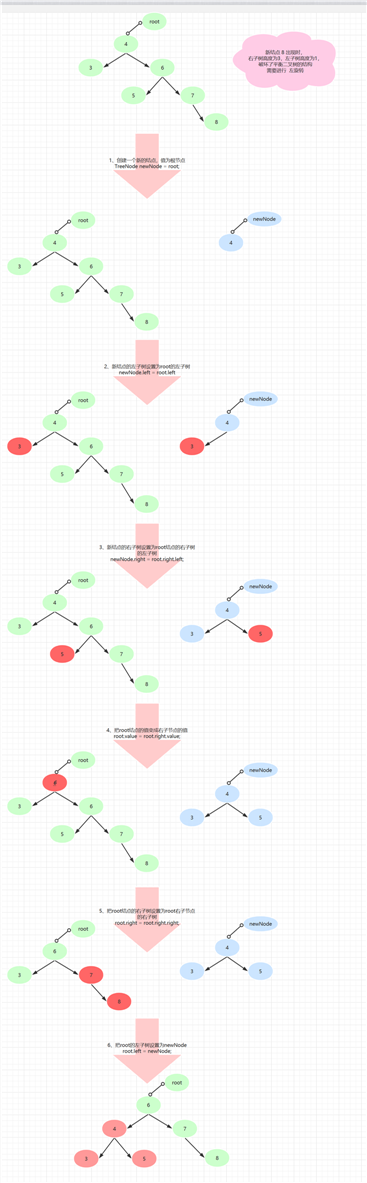

public void leftRotate(){ ? // 1、创建一个新结点,值为当前结点的值 TreeNode newNode = new TreeNode(val); // 2、新结点的左子树 设置为 当前结点的左子树 newNode.left = left; // 3、新结点的右子树 设置为 当前结点右子结点的左子树 newNode.right = right.left; // 4、把当前结点的值 设置为 当前结点 右子节点的值 val = right.val; // 5、把当前结点的右子树 设置为 右子节点 的右子树 right = right.right; // 6、把当前结点的左子树 设置为 新结点 left = newNode; ? }
数列10,12,8,9,7,6
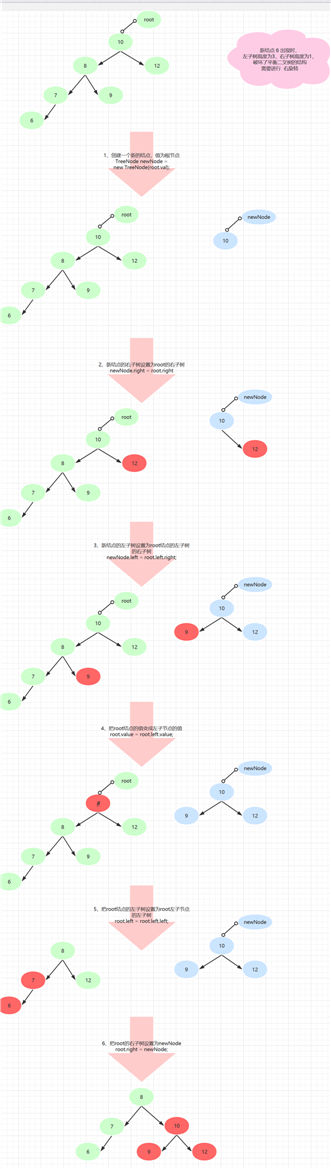

public void rightRotate(){ ? // 1、创建一个新结点,值为当前结点 TreeNode newNode = new TreeNode(val); // 2、把新结点的右子树 设置为 当前结点的右子树 newNode.right = right; // 3、把新结点的左子树 设置为 当前结点的左子树的右子树 newNode.left = left.right; // 4、把当前结点的值 设置为 当前结点的左子结点的值 val = left.val; // 5、把当前结点的左子树 设置为 当前结点的左子结点的左子树 left = left.left; // 6、把当前结点的右子树 设置为 新结点 right = newNode; ? }
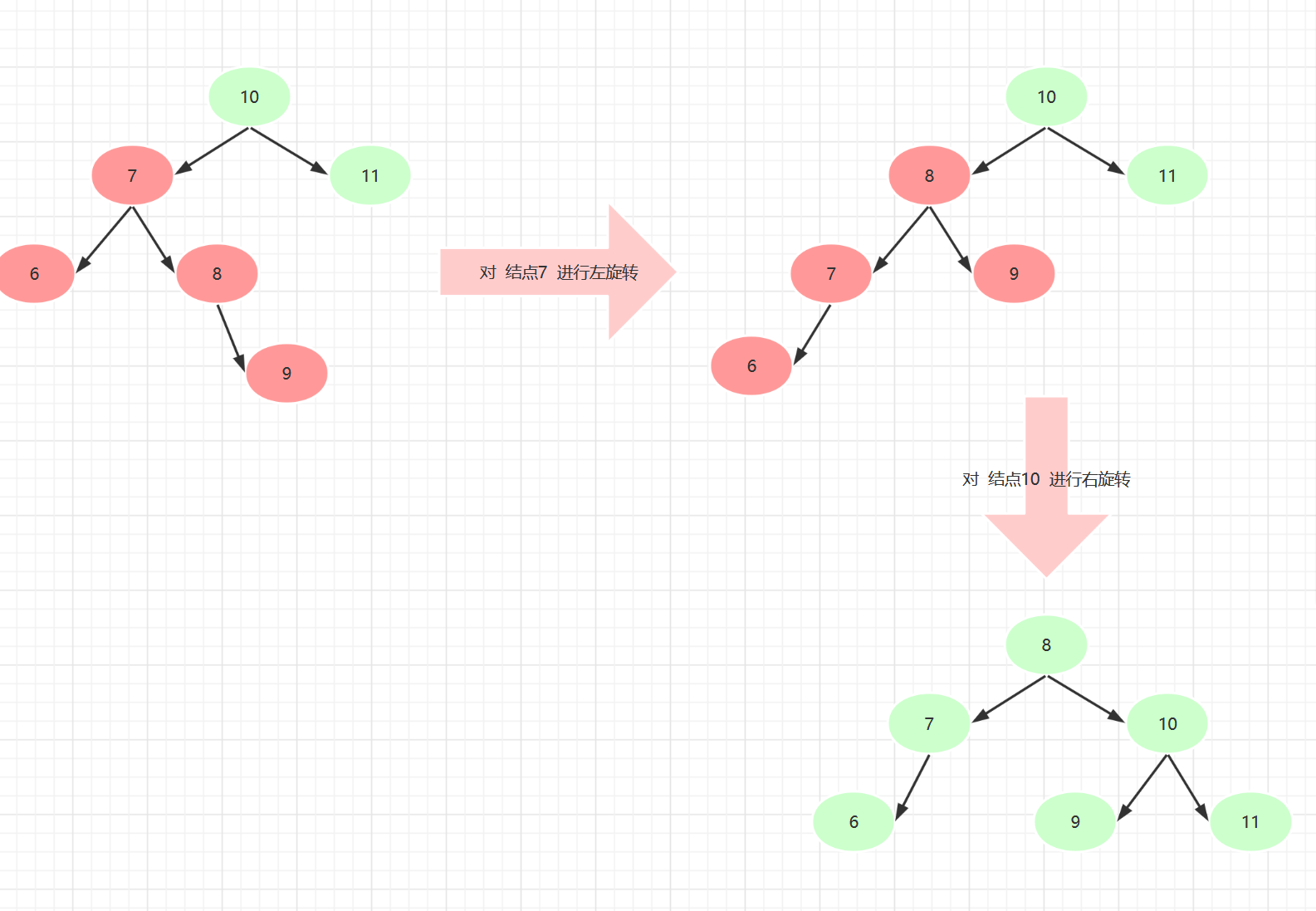
数列10,11,7,6,8,9
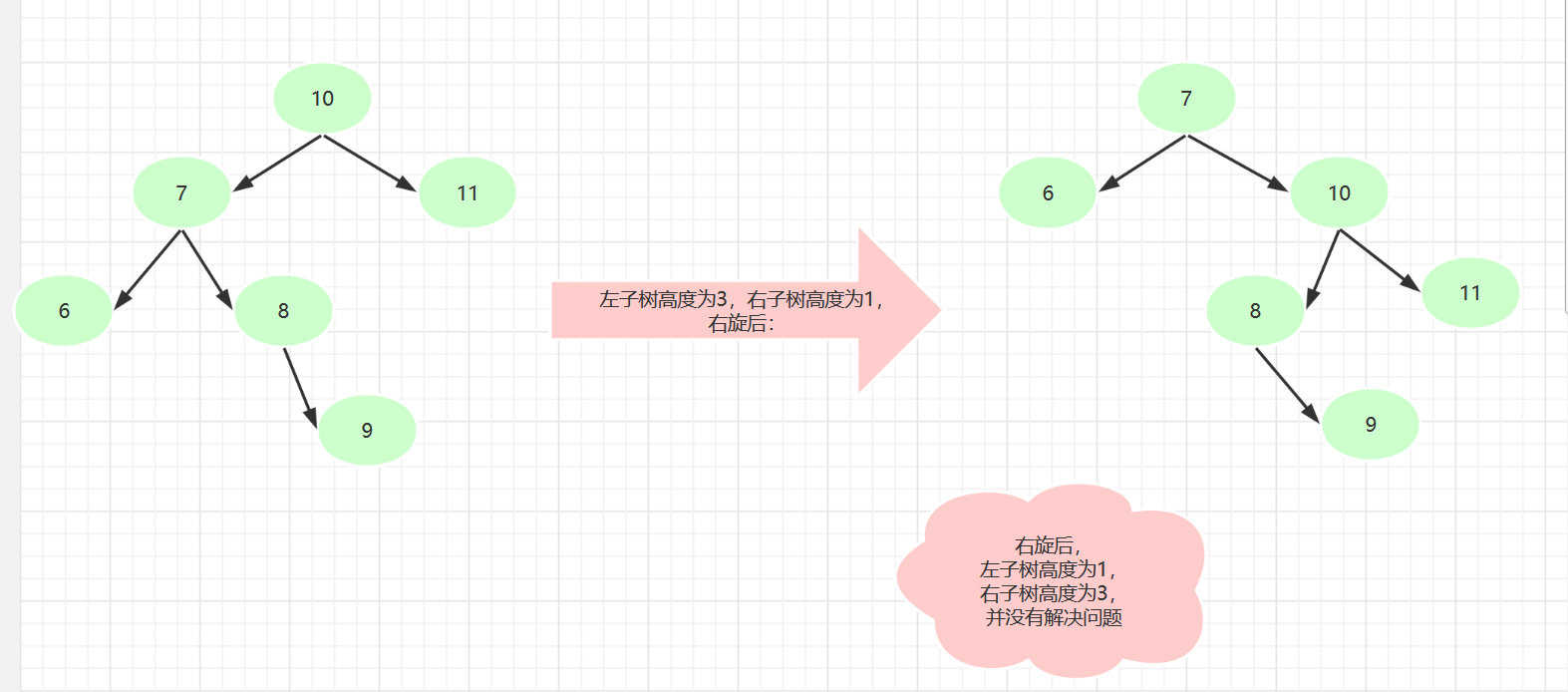
根节点的左子节点的 右子树的高度 大于 左子树的高度
根节点的左子节点的 右子树的高度 = 2
根节点的左子节点的 左子树的高度 = 1
先对根节点的左子树进行 左旋转
再对根节点进行 右旋转
数列2,1,6,5,7,3
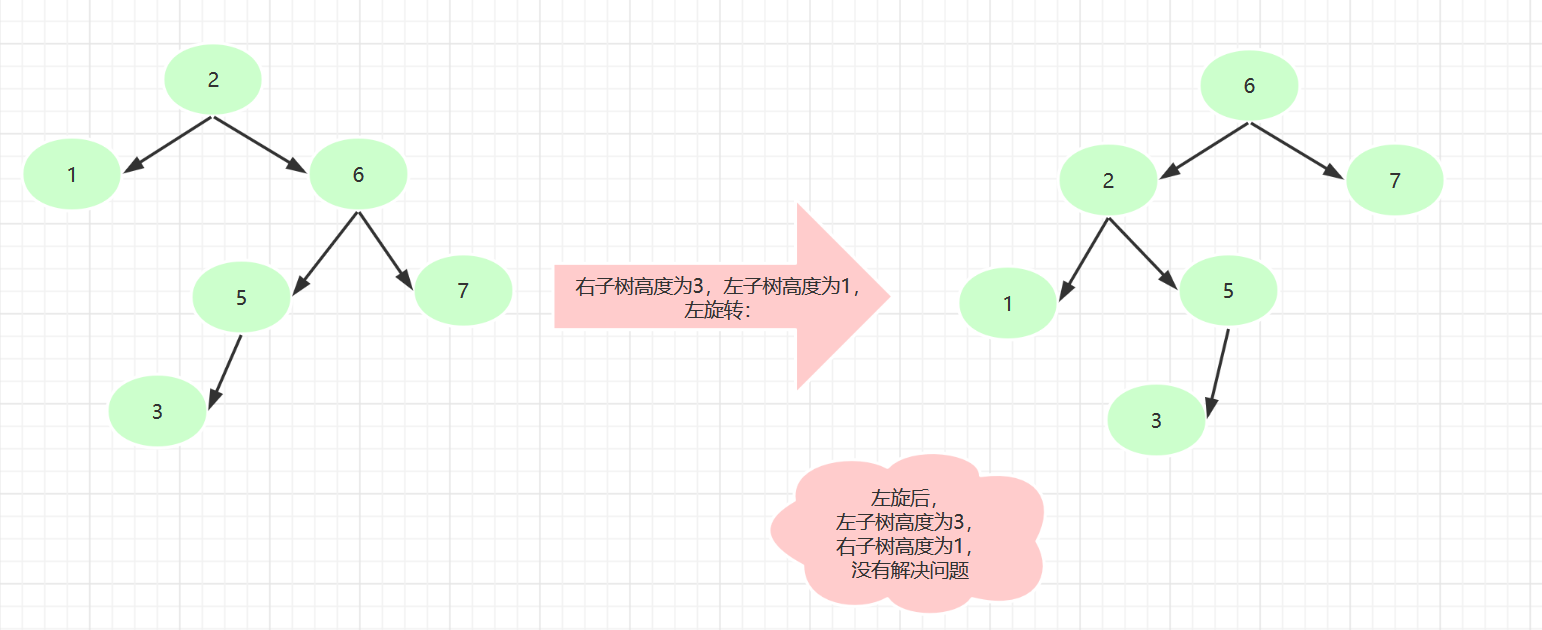
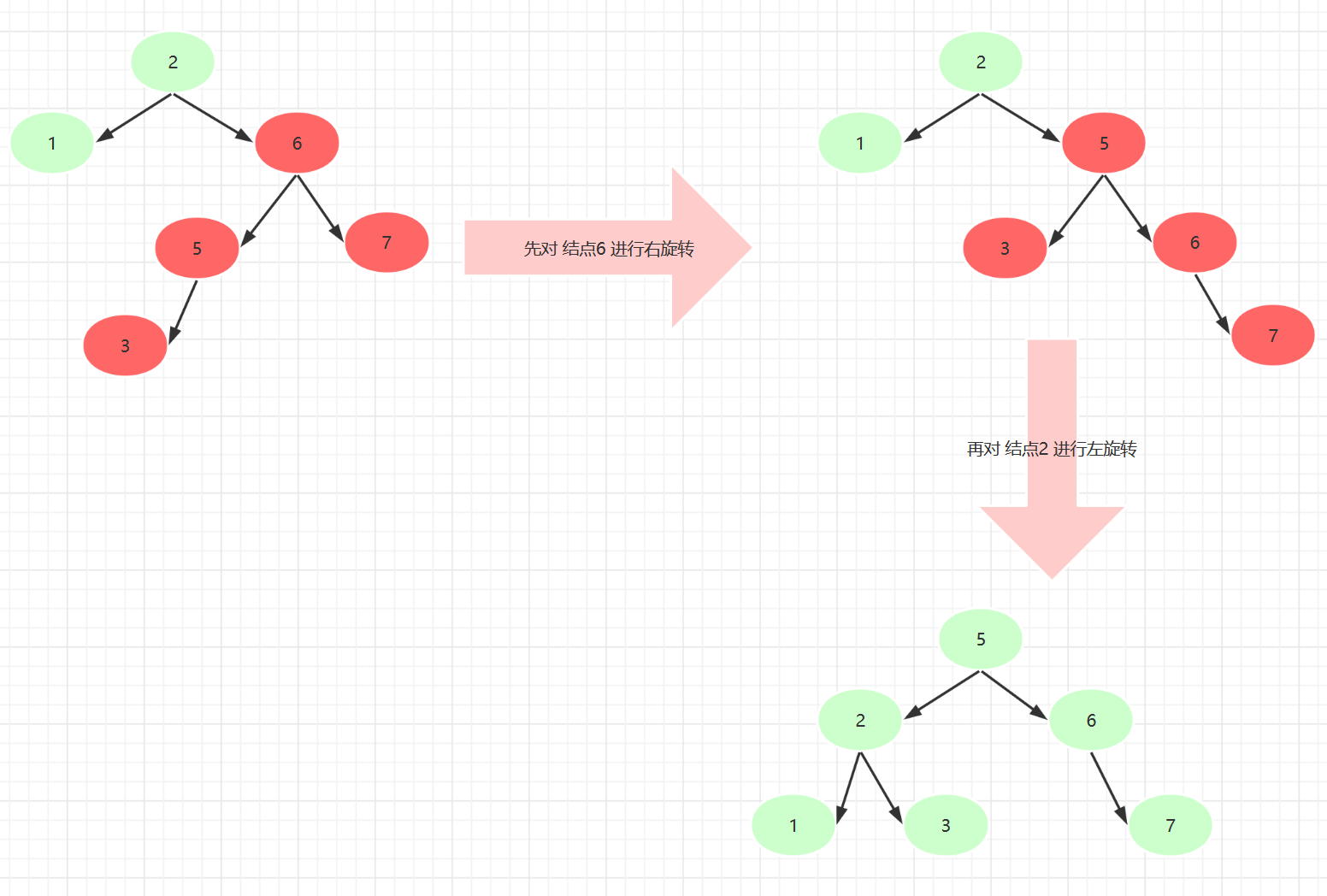
根节点的右子结点的 左子树的高度 大于 右子树的高度
根节点的右子结点的 左子树的高度 = 3
根节点的右子结点的 右子树的高度 = 1
先对根节点的右子节点进行右旋转
再对根节点进行左旋转

// 左旋 if((rightHeight() - leftHeight()) > 1){ // 判定当前节点的右子节点的 左子树的高度 是否大于 右子树的高度 if (right.leftHeight() > right.rightHeight()){ right.rightRotate(); } leftRotate(); } ? // 右旋 if (leftHeight() - rightHeight() > 1){ // 判定当前结点左子结点的 右子树的高度 是否大于 左子树的高度 if(left != null && left.rightHeight() > left.leftHeight()){ // 对当前结点的左子树进行左旋转 left.leftRotate(); } rightRotate(); }
public class AVLTree {
?
// 树结点
private static class TreeNode{
?
int val;
TreeNode left;
TreeNode right;
?
public TreeNode(int val) {
this.val = val;
}
?
// 返回结点的高度
public int height(){
return Math.max(left == null ? 0 : left.height(), right == null? 0 : right.height()) + 1;
}
?
// 返回左子树的高度
public int leftHeight(){
if (left == null){
return 0;
}
return left.height();
}
?
// 返回右子树的高度
public int rightHeight(){
if (right == null){
return 0;
}
return right.height();
}
?
// 左旋
public void leftRotate(){
?
// 1、创建一个新结点,值为当前结点的值
TreeNode newNode = new TreeNode(val);
// 2、新结点的左子树 设置为 当前结点的左子树
newNode.left = left;
// 3、新结点的右子树 设置为 当前结点右子结点的左子树
newNode.right = right.left;
// 4、把当前结点的值 设置为 当前结点 右子节点的值
val = right.val;
// 5、把当前结点的右子树 设置为 右子节点 的右子树
right = right.right;
// 6、把当前结点的左子树 设置为 新结点
left = newNode;
?
}
?
// 右旋
public void rightRotate(){
?
// 1、创建一个新结点,值为当前结点
TreeNode newNode = new TreeNode(val);
// 2、把新结点的右子树 设置为 当前结点的右子树
newNode.right = right;
// 3、把新结点的左子树 设置为 当前结点的左子树的右子树
newNode.left = left.right;
// 4、把当前结点的值 设置为 当前结点的左子结点的值
val = left.val;
// 5、把当前结点的左子树 设置为 当前结点的左子结点的左子树
left = left.left;
// 6、把当前结点的右子树 设置为 新结点
right = newNode;
}
?
// 根据二叉排序树的规则添加结点
public void add(TreeNode newNode){
?
if (newNode == null){
return ;
}
?
/**
* 如果当前新结点的值大于当前结点this
* 如果当前结点右子树为空,直接添加
* 否则,右子树重新调用add方法,重复此步骤
*/
if (newNode.val >= this.val){
if (this.right == null){
this.right = newNode;
}else {
this.right.add(newNode);
}
}else {
if (this.left == null){
this.left = newNode;
}else {
this.left.add(newNode);
}
}
?
// 左旋
if((rightHeight() - leftHeight()) > 1){
// 判定当前节点的右子节点的 左子树的高度 是否大于 右子树的高度
if (right.leftHeight() > right.rightHeight()){
right.rightRotate();
}
leftRotate();
}
?
// 右旋
if (leftHeight() - rightHeight() > 1){
// 判定当前结点左子结点的 右子树的高度 是否大于 左子树的高度
if(left != null && left.rightHeight() > left.leftHeight()){
// 对当前结点的左子树进行左旋转
left.leftRotate();
}
rightRotate();
}
}
?
}
?
// AVL树
private static class AVL{
?
// 根节点
private TreeNode root;
?
// 添加结点
public void add(TreeNode node){
// root为空,说明node为构建树的第一个结点
if (root == null){
root = node;
}else {
root.add(node);
}
}
?
// 返回左子树高度
public int leftHeight(TreeNode node){
if (node == null){
return 0;
}
return node.leftHeight();
}
?
// 返回右子树高度
public int rightHeight(TreeNode node) {
if (node == null) {
return 0;
}
return node.rightHeight();
}
?
// 返回树的高度
public int height(TreeNode node){
if (node == null) {
return 0;
}
return node.height();
}
?
}
?
}
标签:代码实现 enc closed nta fence line pen lazy 常见
原文地址:https://www.cnblogs.com/LittleSkinny/p/14419452.html