标签:不等式 最大 rgba cut gui 分解 loading tps while

思路:
1.动态规划
首先想到的肯定是暴力解法,将所有情况列举出来再计算,时间复杂度O(2^n),很明显这种做法会超时。
如何改进暴力解法呢?在计算时会发现暴力解法实际上是将求解F(n)的问题分解成求解F(n-1)的问题。
由此可以使用动态规划的解法。
定义一个数组dp,其中 dp[i] 表示的是长度为 i 的绳子能得到的最大乘积。我们先把长度为 i 的绳子拆成两部分,一部分是 j,另一部分是 i-j,那么会有下面4种情况:
1. j,i-j 都不可拆
dp[ i ] = ( i - j ) * j
2. j 可拆,i-j 不可拆
dp[ i ] = ( i - j ) * dp[ j ]
3. j 不可拆,i-j 可拆
dp[ i ] = dp[ i - j ] * j
4. j,i-j 都可拆
dp[ i ] = dp[ i - j ] * dp[ j ]
取这4种里的最大值,代码如下:
class Solution { public int cuttingRope(int n) { int[] dp = new int[n+1]; dp[1] = 1; for (int i = 2; i<=n; i++){ for (int j = 1; j < i; j++){ int a = dp[i]; int b = (i-j)*j; int c = (i-j)*dp[j]; int d = dp[i-j]*j; int e = dp[i-j]*dp[j]; dp[i] = Math.max(a,Math.max(Math.max(b,c),e)); } } return dp[n]; } }
2. 数学方法
由算术几何均值不等式可知,当所有绳段长度相等时,乘积最大。
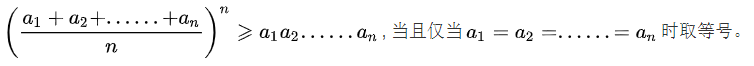
如果把长度为n的绳子分为x段,则每段只有在长度相等的时候乘积最大,那么每段的长度是n/x,他们的乘积是(n/x)^x。
对函数求导,当x=n/e的时候,也就是每段绳子的长度是 n/x=n/(n/e)=e 的时候乘积最大。
而题中绳子剪的长度都是整数,所以只能取接近e的值,也就是3的时候乘积最大。
这里也有例外,当 n≤4 时,因为2×2>1×3,有特殊情况。
因此如果n大于4,就不停的把绳子减去3,代码如下:
public int cuttingRope(int n) { if (n == 2 || n == 3) return n - 1; int res = 1; while (n > 4) { //如果n大于4,我们不停的让他减去3 n = n - 3; //计算每段的乘积 res = res * 3; } return n * res; } 参考: https://leetcode-cn.com/problems/jian-sheng-zi-lcof/solution/shu-xue-zhi-shi-he-dong-tai-gui-hua-liang-chong-fa/
标签:不等式 最大 rgba cut gui 分解 loading tps while
原文地址:https://www.cnblogs.com/zccfrancis/p/14425607.html