LeetCode-766. Toeplitz Matrix（托普利茨矩阵）

标签：limited   element   int   inpu   elements   loading   怎么   存储   否则   

托普利茨矩阵

给你一个 m x n 的矩阵 matrix 。如果这个矩阵是托普利茨矩阵，返回 true ；否则，返回 false 。
如果矩阵上每一条由左上到右下的对角线上的元素都相同，那么这个矩阵是托普利茨矩阵 。
示例1

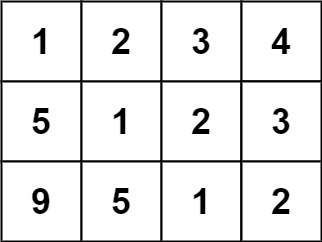
输入：matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
输出：true
解释：
在上述矩阵中, 其对角线为:
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]"。
各条对角线上的所有元素均相同, 因此答案是 True

示例2

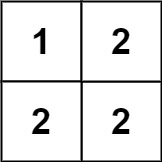
输入：matrix = [[1,2],[2,2]]
输出：false
解释：
对角线 "[1, 2]" 上的元素不同

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 20
• 0 <= matrix[i][j] <= 99

进阶：

1. 如果矩阵存储在磁盘上，并且内存有限，以至于一次最多只能将矩阵的一行加载到内存中，该怎么办？
2. 如果矩阵太大，以至于一次只能将不完整的一行加载到内存中，该怎么办？

Toeplitz Matrix

Given an m x n matrix, return true if the matrix is Toeplitz. Otherwise, return false.
A matrix is Toeplitz if every diagonal from top-left to bottom-right has the same elements.
Example 1:

Input: matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
Output: true
Explanation:
In the above grid, the diagonals are:
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]".
In each diagonal all elements are the same, so the answer is True.

example 2

Input: matrix = [[1,2],[2,2]]
Output: false
Explanation:
The diagonal "[1, 2]" has different elements.

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 20
• 0 <= matrix[i][j] <= 99

Follow up:

1. What if the matrix is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
2. What if the matrix is so large that you can only load up a partial row into the memory at once?

解

我们只需要遍历矩阵时，把当前元素与其左上角的元素比较即可。

class Solution {
   public:
    bool isToeplitzMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                if (matrix[i][j] != matrix[i - 1][j - 1]) {
                    return false;
                }
            }
        }
        return true;
    }
};

进阶1
一次最多只能将矩阵的一行加载到内存中，我们将每一行复制到一个连续数组中，随后在读取下一行第一个元素时，把内存中用不到最后一位调出内存即可，新调入的就与内存中此前保存的数组进行比较。
进阶2
一次只能将不完整的一行加载到内存中，我们将整个矩阵竖直切分成若干子矩阵，并保证两个相邻的矩阵至少有一列或一行是重合的，然后判断每个子矩阵是否符合要求。

LeetCode-766. Toeplitz Matrix（托普利茨矩阵）

标签：limited   element   int   inpu   elements   loading   怎么   存储   否则   

原文地址：https://www.cnblogs.com/qdcs2000/p/14429238.html