标签：director   double   pen   imu   erro   int   读取   sop   exchange   

一、 群的性质

1. {Z,+} 是否为群？若是，验证其满足群定义；若不是，说明理由。
2. {N,+} 是否为群？若是，验证其满足群定义；若不是，说明理由。

其中 Z 为整数集，N 为自然数集。

1）{Z,+}为群

封闭性验证: \(\forall a_1,a_2 \in Z\), 仍有\(a_1+a_2\in Z\)

结合率验证：\(\forall a_1,a_2,a_3 \in Z\), 有\((a_1+a_2) + a_3 = a_1+(a_2 + a_3)\)

幺元验证: 当\(a_0 = 0\) , \(a_0 \in Z\)，有\(\forall a \in Z\)，\(a_0+a=a+a_0=a\)

逆验证：\(\forall a \in Z\)， 存在\(\forall a^{-1} \in Z\)，\(a+a^{-1} = a_0\)

1）{N,+} 为群

封闭性验证: \(\forall a_1,a_2 \in N\), 仍有$a_1+a_2\in $N

结合率验证：\(\forall a_1,a_2,a_3 \in N\), 有\((a_1+a_2) + a_3 = a_1+(a_2 + a_3)\)

幺元验证: 当\(a_0 = 0\) , \(a_0 \in N\)，有\(\forall a \in Z\)，\(a_0+a=a+a_0=a\)

逆验证：\(\forall a \in N\)， 存在\(\forall a^{-1} \in N\)，\(a+a^{-1} = a_0\)

二、验证向量叉乘的李代数性质

我们说向量和叉乘运算构成了李代数，现在请你验证它。书中对李代数的定义为：李代数由一个集合 V，一个数域 F 和一个二元运算 [,] 组成。如果它们满足以下几条性质，称 (V,F,[,]) 为一个李代数，记作 g。

请验证 \(g = (R^3,R,×)\) 构成李代数。

证：

设有 \(\vec{a}=( a_{1},a_{2},a_{3} )\) 和 \(\vec{b}=( b_{1},b_{2},b_{3} )\)，其中 \(\vec{a}, \vec{b} \in {R}^{3}\)

1）封闭性验证：

? \(\vec{a}\times \vec{b}=\left [ \begin{matrix} i & j &k \\ a_{1} & a_{2} & a_{3}\\ b_{1} & b_{2} & b_{3} \end{matrix} \right ]=\left [ \begin{matrix} a_{2}b_{3}-a_{3}b_{2}\\ a_{3}b_{1}-a_{1}b_{3}\\ a_{1}b_{2}-a_{2}b_{1} \end{matrix} \right ] \in {R}^{3}\)

2）双线性验证：

设\(\vec{c}=\left ( c_{1},c_{2},c_{2} \right ) \in {R}^{3}\)，\(\alpha , \beta \in {R}\)。则：

\(( \alpha \vec{a}+\beta \vec{b} )\times \vec{c}=\left [ \begin{matrix} i & j & k\\ \alpha a_{1}+\beta b_{1} & \alpha a_{2}+\beta b_{2} & \alpha a_{3}+\beta b_{3}\\ c_{1} & c_{2} & c_{3} \end{matrix} \right ]\\ =\left ( \alpha a_{2}c_{3}-\alpha a_{3}c_{2} \right )i+\left ( \beta b_{2}c_{3}-\beta b_{3}c_{2} \right )i+(\alpha a_{3}c_{1}-\alpha a_{1}c_{3})j+\left ( \beta b_{3}c_{1}-\beta b_{1}c_{3} \right )j +\left ( \alpha a_{1}c_{2}-\alpha a_{2}c_{1} \right )k\\+\left ( \beta b_{1}c_{2}-\beta b_{2}c_{1} \right )k\\ =\alpha\left [ \begin{matrix} i & j &k \\ a_{1} & a_{2} & a_{3}\\ c_{1} & c_{2} & c_{3} \end{matrix} \right ]+\beta \left [ \begin{matrix} i & j & k\\ b_{1} & b_{2} &b_{3} \\ c_{1} & c_{2} & c_{3} \end{matrix} \right ]\\=\alpha \vec{a}\times\vec{c}+\beta \vec{b} \times \vec{c}\)

同理，\(\vec{c} \times ( \alpha \vec{a}+\beta \vec{b} )=\alpha\left ( \vec{c} \times \vec{a} \right ) + \beta ( \vec{c} \times \vec{b} )\)

3）自反性验证：

? \(\vec{a} \times \vec{a} = 0\)

4）雅克比等价性验证：

? \(\vec{a} \times(\vec{b} \times \vec{c} ) +\vec{c} \times (\vec{a} \times \vec{b} ) +\vec{b} \times \left(\vec{c} \times \vec{a} \right ) =0\)

所以\(g = (R^3,R,×)\) 构成李代数。

三、推导 SE(3) 的指数映射

课上给出了 SO(3) 的指数映射推导，但对于 SE(3)，仅介绍了结论，没有给出详细推导。请你完成 SE(3) 指数映射部分，有关左雅可比的详细推导。

设 \(ξ = [ρ,?]^T ∈ se(3)\)，它的指数映射为：

? \(exp(\xi ^{\wedge}) = \begin{bmatrix} \sum_{n=0}^{\infty }\frac{1}{n!}(\phi ^\wedge)^n & \sum_{n=0}^{\infty }\frac{1}{(n+1)!}(\phi ^\wedge)^n\rho \\ 0^T & 1 \end{bmatrix}\)

令 \(? = θa\)，那么：

\(\sum_{n=0}^{\infty }\frac{1}{(n+1)!}(\phi ^\wedge)^n = \sum_{n=0}^{\infty }\frac{1}{(n+1)!}(θa ^\wedge)^n\)

Taylor展开

\(\sum_{n=0}^{\infty }\frac{1}{(n+1)!}(θa ^\wedge)^n = I + \frac{1}{2!}θa^\wedge + \frac{1}{3!}θ^2{a^\wedge}^2 + ... + \frac{1}{(n+1)!}θ^n{a^\wedge}^n \\=aa^T - a^\wedge a^\wedge + \frac{1}{2!}θa^\wedge + \frac{1}{3!}θ^2{a^\wedge}^2 + ... \\ = aa^T - \frac{(θ - \frac{1}{3!}θ^3 + \frac{1}{5!}θ^5 - ...)a^\wedge a^\wedge}{θ}+ \frac{(\frac{1}{2!}θ^2 - \frac{1}{4!}θ^4 + ...)a^\wedge }{θ}\\ = a^\wedge a^\wedge + I - \frac{\sin θ a^\wedge a^\wedge}{θ}-\frac{\cos θ a^\wedge}{θ} + \frac{a^\wedge}{θ} \\ = (1-\frac{\sin \theta}{\theta})a^\wedge a^\wedge + (\frac{1-\cos \theta }{\theta})a^\wedge + I \\= (1-\frac{\sin \theta}{\theta})(a a^T-I) + (\frac{1-\cos \theta }{\theta})a^\wedge + I \\ = \frac{\sin \theta}{\theta}I + (I-\frac{\sin\theta}{\theta})aa^T + (\frac{1-\cos \theta }{\theta})a^\wedge\)

四、伴随

在 SO(3) 和 SE(3) 上，有一个东西称为伴随（Adjoint）。下面请你证明 SO(3) 伴随的性质。 对于 SO(3)，有：

? \(Rexp(p^∧)R^T = exp((Rp)^∧)\)

此时称 \(Ad(R) = R\)。

提示：首先你需要证明\(?a ∈R^3,Ra^∧R^T = (Ra)^∧\)，参考

Taylor展开\(exp(p^∧)\)，可得

\(Rexp(p^∧)R^T = R\sum_{n=0}^{\infty }\frac{{p^∧}^{n}}{n!}R^T = \sum_{n=0}^{\infty }\frac{(R{p^∧}R^T)^{n}}{n!} = exp(Rp^∧R^T) = exp((Rp)^∧)\)

五、轨迹的描绘

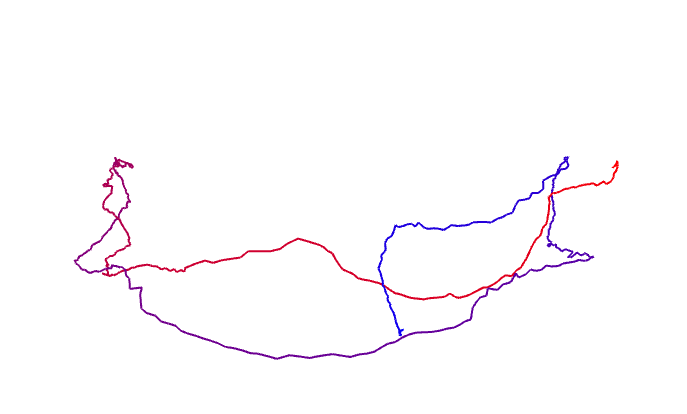
我们通常会记录机器人的运动轨迹，来观察它的运动是否符合预期。大部分数据集都会提供标准轨迹 以供参考，如 kitti、TUM-RGBD 等。这些文件会有各自的格式，但首先你要理解它的内容。记世界坐标系为 W，机器人坐标系为 C，那么机器人的运动可以用 \(T_{WC}\) 或 \(T_{CW}\) 来描述。现在，我们希望画出机器 人在世界当中的运动轨迹，请回答以下问题：

1.事实上，\(T_{WC}\) 的平移部分即构成了机器人的轨迹。它的物理意义是什么？为何画出 \(T_{WC}\)的平移部分就得到了机器人的轨迹？

\(T_{WC}\) 代表的是机器人的相机 C 相对世界坐标系 W 的变换矩阵，世界坐标系 W 相对于 相机 C 是固定不动的。

\(T_{WC}\)的平移部分就得到了机器人的轨迹，是因为机器人的方向由旋转矩阵R决定，而平移是机器人的运动量，该运动量就代表了其运动轨迹。

2.我为你准备了一个轨迹文件（code/trajectory.txt）。该文件的每一行由若干个数据组成，格式为

? \([t,t_x,t_y,t_z,q_x,q_y,q_z,q_w]\),
其中 t 为时间，$t_x,t_y,t_z $为 \(T_{WC}\) 的平移部分，\(q_x,q_y,q_z,q_w\) 是四元数表示的 \(T_{WC}\) 的旋转部分，\(q_w\) 为四元数实部。同时，我为你提供了画图程序 draw_trajectory.cpp 文件。该文件提供了画图部分的代码，请你完成数据读取部分的代码，然后书写 CMakeLists.txt 以让此程序运行起来。注意我们需要用到 Pangolin 库来画图，所以你需要事先安装 Pangolin（如果你做了第一次作业，那么现 在已经安装了）。CMakeLists.txt 可以参照 ORB-SLAM2 部分。

CMakeLists.txt:

cmake_minimum_required( VERSION 2.8 )
project ( draw_trajectory )

set( CMAKE_CXX_COMPILER "g++" )
set( CMAKE_BUILD_TYPE "Release" )
set( CMAKE_CXX_FLAGS "-std=c++11 -march=native -O3" )

############### dependencies ######################
#Pangolin
find_package(Pangolin)
include_directories( ${Pangolin_INCLUDE_DIRS})
# Eigen
include_directories( "/usr/include/eigen3" )
# Sophus 
find_package( Sophus REQUIRED )
include_directories( ${Sophus_INCLUDE_DIRS} )


add_executable(draw_trajectory draw_trajectory.cpp)
target_link_libraries(draw_trajectory
            ${EIGEN3_LIBS}
            ${Pangolin_LIBRARIES}
            ${Sophus_LIBRARIES}
         )

add_executable(draw_gt_est draw_gt_est.cpp)
target_link_libraries(draw_gt_est
            ${EIGEN3_LIBS}
            ${Pangolin_LIBRARIES}
            ${Sophus_LIBRARIES}
         )

CODE:

    ifstream f(trajectory_file);
    while(!f.eof()) {
        Eigen::Vector3d t_tra;
        double t, t_x, t_y, t_z, q_x, q_y, q_z, q_w;
        f >> t >> t_x >> t_y >> t_z;
        t_tra << t_x, t_y, t_z;
        f >> q_x >> q_y >> q_z >> q_w;
        Eigen::Quaterniond q(q_w, q_x, q_y, q_z);
        poses.push_back(Sophus::SE3(q, t_tra));
    }

RESULT:

kieranych@kieranych-ThinkPad-Edge-E431:~/vslam/hw3/code/build$ ./draw_trajectory

六、轨迹的误差

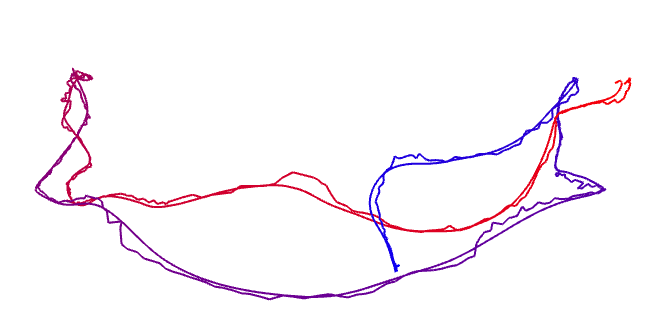
除了画出真实轨迹以外，我们经常需要把 SLAM 估计的轨迹与真实轨迹相比较。下面说明比较的原 理，请你完成比较部分的代码实现。 设真实轨迹（ground-truth）为 Tg，估计轨迹 Te。它们都以 TWC 的形式存储，格式同上题。现在，你 需要计算估计轨迹的误差。我们假设每一个 Tg 都与给定的 Te 对应。那么，对于任意第 i 个位姿，它的误 差可定义为：

? \(e_i = ∥log({T_{gi}}^{-1} T_{ei})^∨∥_2\)

即两个位姿之差的李代数二范数。于是，可以定义两条轨迹的均方根（Root-Mean-Square-Error, RMSE） 误差为：

? $RMSE(g,e) =\sqrt{\frac{1}{n}\sum_{i=1}^{n}e_i2} $

我为你准备了 code/ground-truth.txt 和 code/estimate.txt 两条轨迹。请你根据上面公式，实现 RMSE 的计算代码，给出最后的 RMSE 结果。作为验算，参考答案为：2.207。

CODE:

   // caculate RMSE
    int num = 0;
    double error = 0, RMSE = 0;
    Eigen::Matrix<double,6,1> tmp;

    for (auto i = 0; i < gt_poses.size() - 1; i++){
        tmp = (gt_poses[i].inverse()*est_poses[i]).log();
        error += tmp.transpose()*tmp;
        num++;
    }
    RMSE = sqrt(error/num);
    cout<<"RMSE: "<<RMSE<<endl;

RULST:

./build/draw_gt_est

kieranych@kieranych-ThinkPad-Edge-E431:~/vslam/hw3/code/build$ ./draw_gt_est 
RMSE: 2.20728

李群与李代数

标签：director   double   pen   imu   erro   int   读取   sop   exchange   

原文地址：https://www.cnblogs.com/yujingxiang/p/14459496.html