标签:dir nal cts sso var 没有 图片 要求 com
Hern\(\‘{a}\)n M. and Robins J. Causal Inference: What If.
这一节介绍了一个confounding的概念, 在观测数据中, confounder往往是让人头疼的存在.
backdoor path: 指的是intervention\(A\)和outcome\(Y\)间的一条路径(没有方向要求), 其中存在一个箭头指向\(A\), 但是没有从\(A\)出发的箭头.
注: 存疑
7.1 The structure of confounding
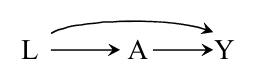
如上图所示, 倘若没有\(L\)的存在, 计算causal effect, 可以直接通过
\[\mathrm{Pr} [Y|A=1] - \mathrm{Pr} [Y|A=0],
\]
来计算, 但是\(L\)的存在导致可交换性不成立, 当然在这个情况下, 我们可以通过standardization, 或者 IP weighting来计算(因为条件可交换性是存在的).
\(L\)是intervention \(A\) 和 预测 \(Y\)的共同的一个cause, 是干扰我们判断的存在, 所以称之为confounder, 这种由\(L\)带来额外的association的现象称之为confounding.
Confounding and exchangeability
这里引入了backdoor criterion的概念, 就是用于判断可交换性是否成立的一个准则.
Confounding and the backdoor criterion
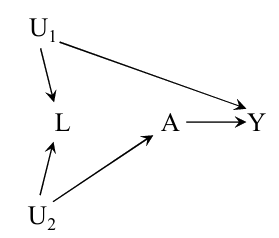
一个非常特殊的情况是, 上图中的\(A \amalg Y\), 但是 \(A \not{\amalg} Y | L\).
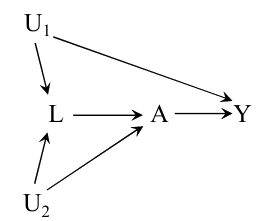
再看上图, 在这种情况下, 无论是否在给定\(L\)的条件下, \(A\)和\(Y\)都是不独立的, 除非给定\(U_1, U_2\).
7.4 Confounding and confounders
7.5 Single-world intervention graphs
介绍了一个更为细致的表示方式: SWIG.
Confounding adjustment
Fine Point
The strength and direction of confounding bias
Identification of conditional and unconditional effects
Surrogate confounders
Confounders cannot be descendants, but can be in the future of treatment
Technical Point
Does conditional exchangeability imply the backdoor criterion?
Fixing the traditional definition of confounder
Difference-in-differences and negative outcome controls
The front door criterion
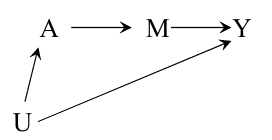
\[\mathrm{Pr}[Y^a=1] =
\sum_m
\mathrm{Pr} [M=m|A=a]
\sum_{a‘}
\mathrm{Pr} [Y=1|M=m,A=a‘]
\mathrm{Pr} [A=a‘].
\]
Chapter 7 Confounding
标签:dir nal cts sso var 没有 图片 要求 com
原文地址:https://www.cnblogs.com/MTandHJ/p/14470513.html



