标签:between 大于 str wav linear sam 滤波器 replicat recover
1.方波采样
square wave的spectrum
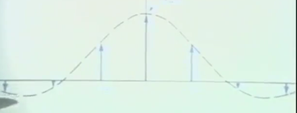
信号经过square wave 采样后的spectrum,时域相乘,频域卷积。
图中可以看到只要采样频率w0 是信号最大频率两倍还大,频谱就不会重叠,信号就能还原.

固定长度,使用Impulse train 作为carrier。

impulse train的频域

原信号

经过
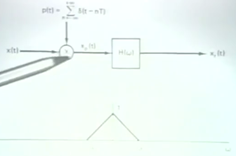
采样后

In other words,When I sample it. the spectrum is replicated.
We can implement exact reconstruction of the original signal by low pass filtering an impulse train whose areas are identical to the sample values.
Essentially this low pass filtering operation provides for us an interpolation in-between the sample values.
2.采样后数据的恢复
采样定理告诉我们,只要采样频率大于等于关心频率的2倍,就能完整的还原原来的信号
一个信号经过采样
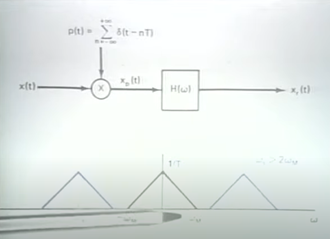
再经过低通滤波器就能得到原来的信号,为啥?
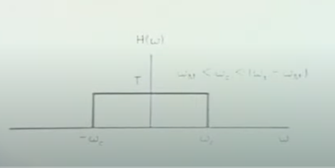
为什么经过低通就能就能得到原来的数据
Xp stands for sampling signal. Xp是采样后的信号
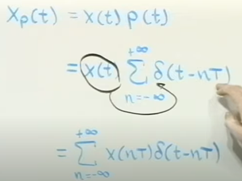
Xr代表recovered signal.
h(t) 这个信号reproduce at each sampling point of the impulses of Xp.
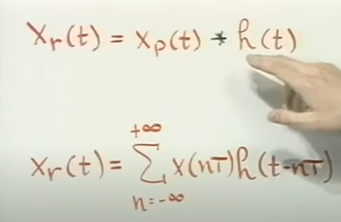
h(t)为理想低通滤波器.
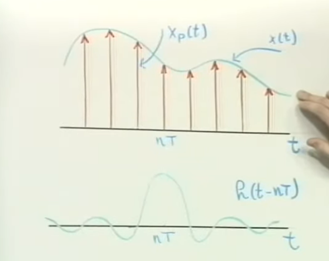
相乘就得到原来的信号了.
3.其他类型的interpolation
Zero order hold
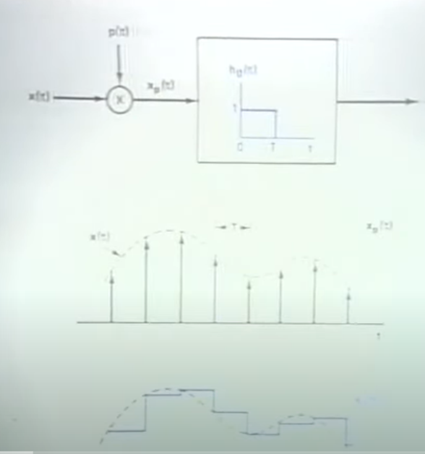
Linear interpolation
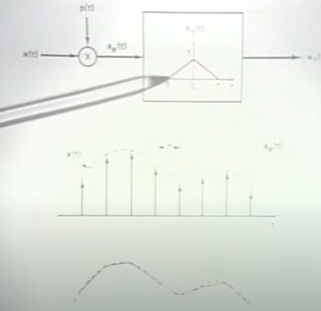
4.采样后的spcreum
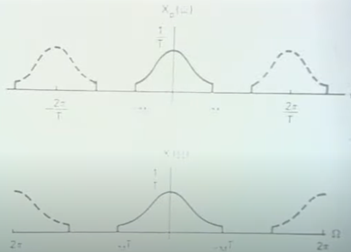
sampling后的连续时间Xp(t)和频谱Xp(w)
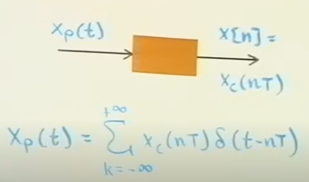
Xp(w) 与X(omega) 一个是连续一个是离散,但是值一样
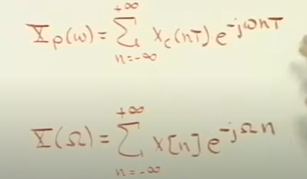
采样后的Xp(w)傅里叶变换和离散时间X(omega)傅里叶变化的关系。
离散时间X(omega)傅里叶是连续时间Xp(w)的stretch T times
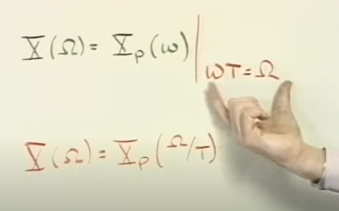
时域分析
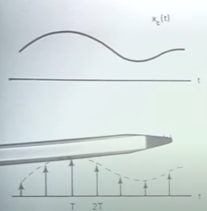
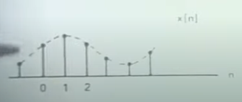
从上图到下图,是一种noromalization, 从1T,2T,3T到数字(1 2 3)
相当于把时间域compress T倍,resacle it from 1T 2T to 1 2.
It means we divide out in time domain by a factor which is the sampling frequency.
Dividing by T in times domain means expand T in frequency domain
If sampling period is doubled. The spacing stretching out by a factor of 2 (上上图).
频域分析
采样后的spctrum
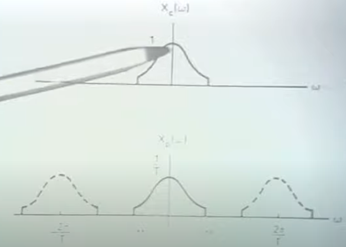
归一化后的spectrum, strech了T倍
5.离散时间采样
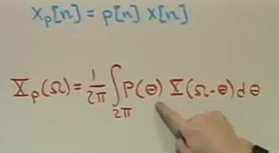
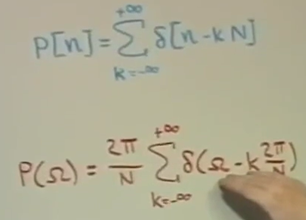
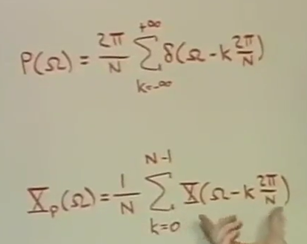
上图是原来的spectrum, 中间是采样spectrum. 下图是采样后的spectrum.

时间分析
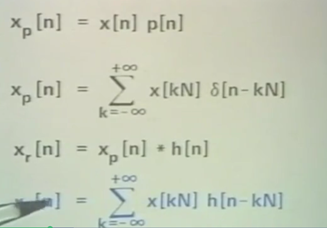
Xd means decimation version
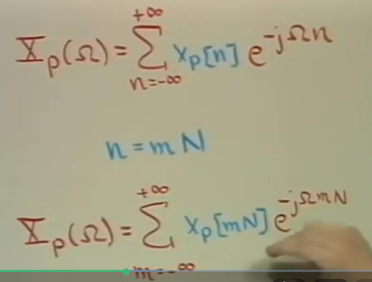
把下面的omega 替代成 omega * N. 上下两个equation equals
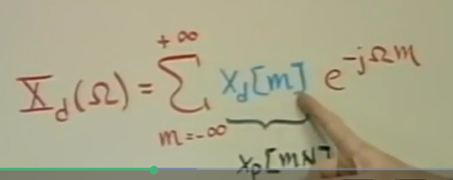
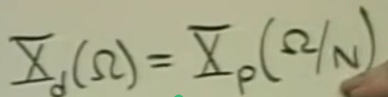
频域分析
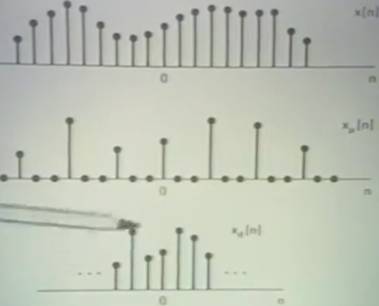
Original signal

After sampling
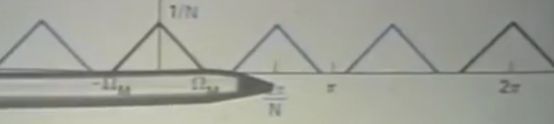
After decimation

标签:between 大于 str wav linear sam 滤波器 replicat recover
原文地址:https://www.cnblogs.com/robsann/p/14487383.html