CF1447E Solution

标签：int   scanf   图片   子节点   lin   题意   name   logs   def   

题目链接

题解

因为要进行异或运算，可以将\(a\)中的数按位存入二叉树中（有些像Trie树）。如题目样例一可存为如下的树：

据题意，\(a_i\)所连的边为与其异或值最小的元素，而该元素在二叉树中一定为与\(a_i\)相邻且与\(a_i\)的LCA最深的叶子节点。如上图中与\(1\)（第4层从左至右数第2个）连边的元素即为其左边的\(0\)。\(n-1\)个间隔位置中连\(n\)条边，一定有至少1条重边，因此实际图中最多有\(n-1\)条有效边，是一个森林。

可以发现，如果存在\(LCA(a_i,a_{i+1})\)（下标为树中顺序）满足其深度小于\(min(LCA(a_{i-1},a_i),LCA(a_{i+1},a_{i+2}))\)，则\(a_i\)与\(a_{i+1}\)之间无法连边，分别在2棵不连通的树中。因此我们希望消除这样的情况，使\(LCA\)单调下降或上升。

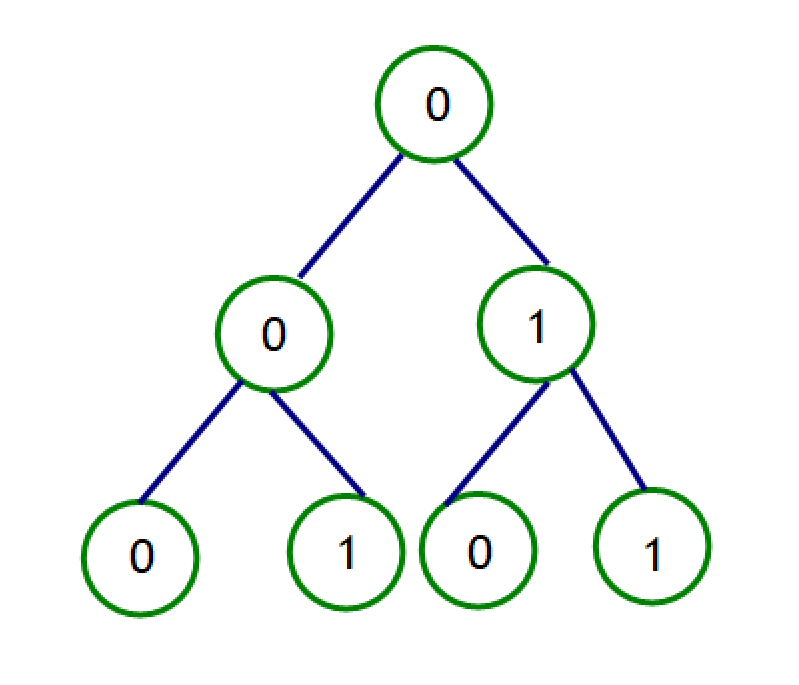
以上图为例，\(LCA(a_i,a_{i+1})\)的深度是先减少后增加的（\(2→1→2\)，根节点深度为\(1\)）。因此对于该图我们需要消除左或右子树中的全部节点，只保留一个叶子节点。例如删去最右侧\(a_4=3\)的叶子节点，则\(LCA(a_{i},a_{i+1})\)变为\(2→1\)。递归分治完成上述操作，保留叶子节点较多的子树即可。

AC代码

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int a[N]; 
int solve(int l,int r,int pos)
{
	if(l>r) return 0;
	if(pos<0) return 1; 
	int mid=r+1;
	for(int i=l;i<=r;i++)
		if(a[i]&(1<<pos)) {mid=i; break;}
	return max(solve(l,mid-1,pos-1)+min(r-mid+1,1),solve(mid,r,pos-1)+min(mid-l,1));
}
int main()
{
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	sort(a+1,a+n+1);
	printf("%d",n-solve(1,n,30));
	return 0;
} 

CF1447E Solution

标签：int   scanf   图片   子节点   lin   题意   name   logs   def   

原文地址：https://www.cnblogs.com/violetholmes/p/14492320.html