【二叉树】leetcode144——二叉树的前序遍历

标签：方便   入栈   参数   tac   pen   树节点   root   lang   return   

编号144：二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

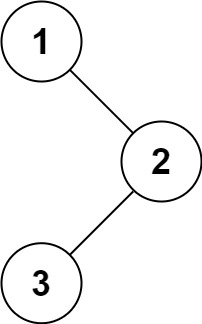
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

思路

具体代码如下：

//Definition for a binary tree node.
type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

• 递归算法

/*递归三部曲
1.确定递归函数的参数和返回值
2.确定终止条件
3.确定单层递归的逻辑
*/

//1.确定递归函数的参数和返回值：因为要打印出前序遍历节点的数值，所以参数里传入[]int类型
//不需要有返回值
func traversal(root *TreeNode, result *[]int) {
	//2.确定终止条件
	if root == nil {
		return
	}

	//3.确定单层递归的逻辑
	//前序遍历 是中 左 右 的顺序，所以先取中间节点的值
	*result = append(*result, root.Val) //中
	traversal(root.Left, result)        //左子树
	traversal(root.Right, result)       //右子树
}

func preorderTraversal(root *TreeNode) []int {
	result := make([]int, 0)
	traversal(root, &result)
	return result
}

• 迭代算法

  前序遍历是中左右，每次先处理的是中间节点，那么先将跟节点放入栈中，然后将右孩子加入栈，再加入左孩子。为什么要先加入 右孩子，再加入左孩子呢？因为这样出栈的时候才是中左右的顺序。

  这里引入了公众号代码随想录的图，方便理解

  

func preorderTraversal(root *TreeNode) []int {
	stack := make([]*TreeNode, 0) //存放二叉树节点
	result := make([]int, 0)      //存放节点数值
	stack = append(stack, root)   //首先将根节点入栈
	for len(stack) != 0 {
		cur := stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		if cur != nil {
			result = append(result, cur.Val) //中
		} else {
			continue //排除叶子节点所指向的左右孩子为空
		}

		stack = append(stack, cur.Right) //右子树进栈
		stack = append(stack, cur.Left)  //左子树进栈
	}
	return result
}

【二叉树】leetcode144——二叉树的前序遍历

标签：方便   入栈   参数   tac   pen   树节点   root   lang   return   

原文地址：https://www.cnblogs.com/zmk-c/p/14492612.html