Leetcode的刷题记录

标签：images   分析   line   部分   matrix   技术   class   前缀和   方便   

长期更新，记录贴。

303 区域和检索

给定一个整数数组 nums，求出数组从索引 i 到 j（i ≤ j）范围内元素的总和，包含 i、j 两点。实现 NumArray 类：NumArray(int[] nums),
使用数组 nums 初始化对象 。int sumRange(int i, int j) 返回数组 nums 从索引 i 到 j（i ≤ j）范围内元素的总和，包含 i、j 两点（也就是 sum(nums[i], nums[i + 1], ... , nums[j])）

求数组的一个子区域的和，暴力计算：每次调用函数进行循环求解。
前缀和：计算\(nums[i]+nums[i+1]+...+nums[j]\)时显然可以用\(sum(nums[0]~nums[j]) - sum(nums[0]~nums[i]) + nums[i]\),这样如果能记录每个元素前面的元素和，要求某个区间内的元素和就可以直接公式计算。因此，直接在初始化数组时记录一个前缀和数组即可。

class NumArray:
    def __init__(self, nums: List[int]):
        self.sums = []  # 记录每一个元素的前缀和
        self.nums = nums
        for i in range(len(nums)):
            if i == 0:
                self.sums.append(nums[0])
            else:
                self.sums.append(self.sums[-1]+nums[i])  # 每次计算到下一个元素，只需要加上该位置元素即可
    def sumRange(self, i: int, j: int) -> int:
        # 计算i到j的元素和，就可以直接调用记录的前缀和数组
        return self.sums[j] - self.sums[i] + self.nums[i]

304 二维矩阵的区域和

给定一个二维矩阵，计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2)

上图子矩阵左上角 (row1, col1) = (2, 1) ，右下角(row2, col2) = (4, 3)，该子矩形内元素的总和为 8。
示例:

给定 matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

和303一样，显然如果要求二维数组某个对角区域和，如果能知道各个点的左上角区域(包含该点)的元素和，那么两个点的对角区域元素和就可以很方便计算。记sum(i,j)为二维数组的左上角(0,0)到点(i,j)的区域元素和，如下图，计算点A和点B的包围区域元素和。从图上可以很直观的看出，AB的区域元素和= B的左上角元素和 - 区域左下角的元素和(不含该点) - 区域右上角的元素和 + A的左上角元素和(不含该点，加它是因为这部分被减去两次)

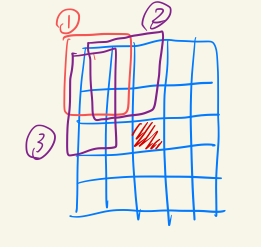
和303问题一样，在初始化时就求出sum(i,j)即可。求前缀和的方法，画图也能直观看出，如下图要求红色点处的左上角区域元素和，可以递归调用，可以两种计算：1）该点对角点的前缀和 + 该点的所在行左边元素和 + 该点所在列的上边元素和 2)该点的左边点的前缀和 + 上边点的前缀和 - 重合区域（对角点的前缀和），即图中的区域②+区域③-区域①。
从分析来看，第一列和第一行的元素的前缀和实际就是一维的情况。然后扩展到二维，依次求出剩下点的前缀和即可。

class NumMatrix:
    def __init__(self, matrix):
        self.sum_mat = matrix  # sum_mat和原数组一样大，存放每个点的前缀和
        # 记录(0,0)到点(i,j)的区域元素和 
        if not len(matrix) == 0:
            # 对于第一行和第一列，是一维问题，直接计算
            for i in range(1,len(matrix)): # 遍历行 的 第一列元素
                # [i][0]处的元素前缀和是 
                self.sum_mat[i][0] = self.sum_mat[i-1][0] + self.sum_mat[i][0]
            for j in range(1,len(matrix[0])):  # di
                self.sum_mat[0][j] = self.sum_mat[0][j-1]  + self.sum_mat[0][j]

            for i in range(1,len(matrix)):
                for j in range(1,len(matrix[0])):
                    # matrix[i][j]表示第i行j列的元素 要求它的左上角邻域元素和  
                    # 它左边点的邻域和 + 上边点的领域和 - 左上角点的邻域和
                    self.sum_mat[i][j] = self.sum_mat[i][j-1] +  self.sum_mat[i-1][j] - self.sum_mat[i-1][j-1] + self.sum_mat[i][j]



    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        # 求任意两点之间的邻域和 等于 
        
        if col1 == 0  and row1 == 0:
            return self.sum_mat[row2][col2]

        if col1 == 0 :
            return self.sum_mat[row2][col2] - self.sum_mat[row1-1][col2]

        if row1 == 0 :
            return self.sum_mat[row2][col2] - self.sum_mat[row2][col1-1]

        p1 = [row2,col1-1]  # 考虑col1就是第一列的情况
        left_bottom = self.sum_mat[p1[0]][p1[1]]
        right_up = self.sum_mat[row1-1][col2] 
        left_up = self.sum_mat[row1-1][col1-1]
        return self.sum_mat[row2][col2] - (left_bottom + right_up - left_up)

Leetcode的刷题记录

标签：images   分析   line   部分   matrix   技术   class   前缀和   方便   

原文地址：https://www.cnblogs.com/muyisun/p/14492598.html