标签:res 梯度下降 enter 也会 eal linear 输出 sim 比较
目前大多数 SR 的 model 都是用的合成下采样图片来进行训练的,而这些合成的图片常常使用的是 MATLAB 里面的 imresize 函数来进行实现的,这样的做法也就是会使得 SR-kernel 是固定和理想。当然还有很多是用各向同性或者各向异性的高斯核作为模糊核通过下式来得到 LR 图像:
不过用这些模糊核合成的图片与真实场景图片都不太符,因此出现往往数据集跑得不错的模型,拿真实场景的图片来测就表现不佳。在现实场景中,即便是同一个 sensor,也会因为手持时细微的相机移动或者 sensor 的光学特性而导致产生不同的 LR。
文章使用了自然场景图片的重要性质:单张图片中的跨尺度小图片块的重现 (recurrence) 性质。基本可以理解为:裁剪出一张图片的图片块 (patch) 和其下采样后图片的图片块 (patch),两张 patch 的大小可能不一样(可能分别是 5*5 和 7*7),但这两张 patch 在像素的分布上大体是一致的。Michaeli & Irani 使用这个性质来估计 SR-Kernel:
the correct SR-kernel is also the downscaling kernel which maximizes the similarity of patches across scales of the LR image.
也就是图片的模糊核是使得 LR 图片中的跨尺度 patch (跨尺度理解为同一张图片的不同分辨率,patch 理解为图片的子图)相似性最大的下采样核。因此只要文章通过 LR 图像找到使得两跨尺度子图相似性最大的 kernel,那该 kernel 就十分接近真实模糊核。
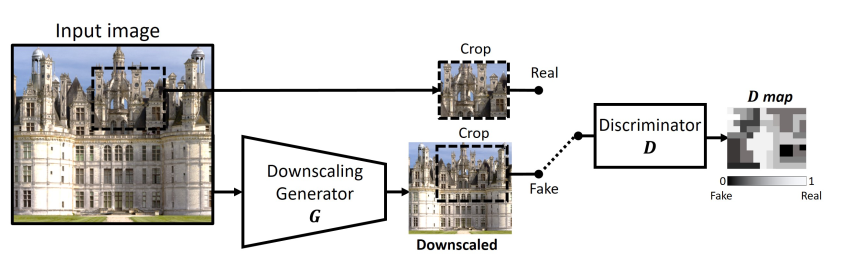
文章提出了 KernelGAN 使用无监督学习来估计 LR 中的模糊核。其具体做法通过生成器生成出低分辨率图像的 s 倍下采样图(s 一般为2),然后裁取一块 patch 作为 Fake 图像,裁取生成器输入的一块 patch 作为 Real 图像,并一起送入判别器中进行判断真假。也就是说生成器可以看作生成 LR 的downscaling 图像的模块,而判别器是用来判别 LR 的 patch 和 LR 下采样图像的 patch 孰真孰假。当判别器难以判别的时候,此时生成器的权重就接近所求的模糊核了。
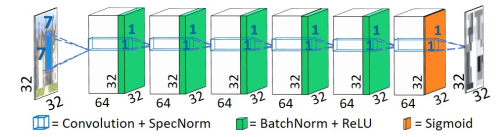
论文提出的判别器全部使用了卷积层,并且卷积层没有使用 stride,除了第一层使用了 7*7 的卷积核,其余层均使用了 1*1 的卷积核,也就是在最后生成的热图 (heat-map) 中的一个值是对输入一个大小为 7*7 的 patch 真假的判断,map 里面的值是 0 到 1 之间(包括端点)的数。输入的 label 取决于输入的真假,如果是真的,label 便全为 1,反之为 0。
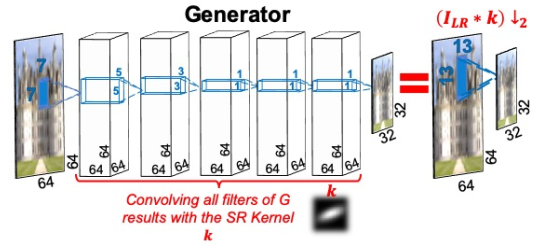
生成器可以理解为一个对输入图片使用了 the downscaling SR-Kernel 进行了下采样的模块。文章认为 downscaling 是由卷积和下采样组成,而这本身是一种线性的变换。文中于是使用的生成器不包含任何非线性的激活函数。

理论上,使用单层卷积层应该可以涵盖所有可能 downscaling 方法的情况,但实验中发现并不能收敛到一个正确的解(如上图)。针对这种情况,文章进行以下推测:
非线性的生成器也是不合适的。生成器没有线性的显式约束,可能会生成一些不想要的结果。这种结果往往生成任何图片都会包含一些跟 downscaling 无关的 patch。
文章于是使用 deep linear networks,并且没有任何的非线性激活函数。虽然说从表达能力来说,深度线性网络和单层线性网络无差。但是在优化过程种,它有多个不同的面,可以使得有无限多个等价的全局最优点,这对于训练更加容易,更快。具体结构如最上面的图,其作用相当于用一个大小为 13*13 的模糊核对 LR 进行 blur 并进行 2 倍下采样。为了提供比较合理的初始点,生成器的输出被与输入经过一种理想的 downscaling 后的图片进行 constrain。一旦生成可以接受的输出后,便不再使用 constraint。
显然单张 LR 图片的 kernel 可以由生成器的权重得到,文章针对为什么要显式地从 生成器中提取 Kernel 进行了说明:
? 我们最终目的是为得到 kernel,而不是得到 downscaling 的网络,并且由生成器提取的 SR-kernel k 是一组小的数组以至于可以应用于 SR 算法之中;
? 显式的提取 kernel 以便于对其进行显式的加入有物理意义的先验操作。
关于第二点文章在 loss 中使用正则项来使提取出的 kernel 满足一些限制,以达到减少一些解看起来正常,实质不行的 kernel:
? kernel 的总和需要为 1;
? kernel 的几何中心必须在正中央位置。
以上两项是为了保证 kernel 不会 shift 图像(应该是不会让图像几何变形)
? kernel 需要有稀疏性,以至于不会 oversmooth;
? kernel 希望越接近边界越接近零,不希望非零值靠近边界。
最后,希望提取是可微的,这样 loss 中的正则化项(因为正则化项是由提取的 kernel 计算的)才能进行反向传播(文中对 G 中所有的 filters 使用 -1 的 stride 进行卷积)。整个网络和正则项的定义如下:
SR-kernel 除了和图片有关,还与下采样的倍数 s 有关。但是对于 SR-kernel 来说不同 scales 之间是有关联的,文章训练的是 scale 为 2 的 SR-kernel,但是可以由此推导出 scale 为 4 的kernel。这使得我们可以由一种 scale 的 kernel 生成多种 scale 的 kernel,并且当需要大 scale (如4)的 kernel 不需要非得去制作 scale 为 4 的 LR 来训练得到相应的 kernel(即便得到了 scale 为 4 的 LR,也会因为其只有 HR 的十六分之一导致包含信息太小而难以训练。
delta = torch.Tensor([1.]).unsqueeze(0).unsqueeze(-1).unsqueeze(-1).cuda()
for ind, w in enumerate(self.G.parameters()):
curr_k = F.conv2d(delta, w, padding=self.conf.G_kernel_size - 1) if ind == 0 else F.conv2d(curr_k, w)
self.curr_k = curr_k.squeeze().flip([0, 1])
文章使用狄拉克函数作为初始输入,使用 G 的每一层卷积核作为提取 kernel 的卷积层的卷积核,得到的输出作为下一层提取 kernel 的卷积层的输入。由于初始值为 1 最后的结果与一张图片所卷积的效果等同于使用 G 中所有卷积层与图片卷积的效果。这便是提取到的最初始的 kernel。
代码位置
Blind Super-Resolution Kernel Estimation using an Internal-GAN 论文解读
标签:res 梯度下降 enter 也会 eal linear 输出 sim 比较
原文地址:https://www.cnblogs.com/froml77/p/14453399.html