codeforces CF981C Useful Decomposition 菊花图性质

标签：mon   描述   iostream   bit   puts   def   byte   接下来   输入输出   

博客迁移计划12

$ \rightarrow $ 戳我看CF原题

C. Useful Decomposition

　
Ramesses knows a lot about problems involving trees
(undirected connected graphs without cycles)!
　
He created a new useful tree decomposition,
but he does not know how to construct it, so he asked you for help!
　
The decomposition is the splitting the edges of the tree in some simple paths in such a way
that each two paths have at least one common vertex. Each edge of the tree should be in exactly one path.
　
Help Remesses, find such a decomposition of the tree or derermine that there is no such decomposition.

Input

The first line contains a single integer $ n (2 \le n \le 10^6) $ the number of nodes in the tree.
　
Each of the next $ n-1 $ lines contains two integers $ a_i $ ans $ b_i (1\le a_i,b_i \le n, a_i \not= b_i ) $
— the edges of the tree. It is guaranteed that the given edges form a tree.

Output

If there are no decompositions, print the only line containing "No".
　
Otherwise in the first line print "Yes", and in the second line print the number of paths in the decomposition $ m $ .
　
Each of the next $ m $lines should contain two integers $ u_i ,v_i (1 \le u_i,v_i \le n, u_i \not= v_i ) $ denoting that
one of the paths in the decomposition is the simple path between nodes $ u_i $ and $ v_i $ .
　
Each pair of paths in the decomposition should have at least one common vertex,
and each edge of the tree should be presented in exactly one path.
You can print the paths and the ends of each path in arbitrary order.
　
If there are multiple decompositions, print any.

Examples

input1

 4
 1 2
 2 3
 3 4

output1

 Yes
 1
 1 4

input2

 6
 1 2
 2 3
 3 4
 2 5
 3 6

output2

 No

input3

 5
 1 2
 1 3
 1 4
 1 5

output3

 Yes
 4
 1 2
 1 3
 1 4
 1 5

Note

The tree from the first example is shown on the picture below:

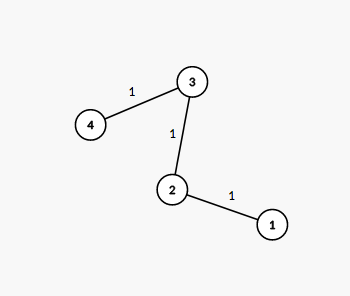
The number next to each edge corresponds to the path number in the decomposition.
It is easy to see that this decomposition suits the required conditions.
　
The tree from the second example is shown on the picture below:

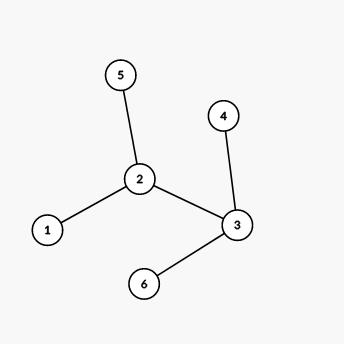
We can show that there are no valid decompositions of this tree.
　
The tree from the third example is shown on the picture below:

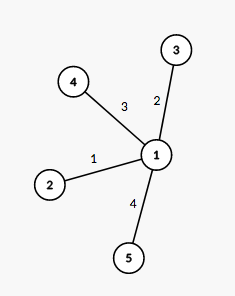
The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.

题目描述

RAMESS知道很多关于树的问题（无循环的无向连通图）！
他创建了一个新的有用的树的划分，但他不知道如何构造它，所以他请求你的帮助！
划分是从树上的边中分裂出一些简单的路径，使得每个两条路径都具有至少一个公共顶点。树的每一个边都应该在一条路径上。
帮助RAMESs，找到这样的树的划分，或判断没有这样的划分。

输入输出格式:

输入格式:

第一行一个整数 $ n $ 表示树上的点个数,树上的点编号从 $ 1~n $。
接下来 $ n-1 $ 行每行两个整数 $ a_i, b_i $ 表示树上有一条从 $ a_i $ 到 $ b_i $ 的边。 $ (1 \le a_i,b_i \le n,a_i \not= b_i) $
　

输出格式:

如果没有划分,只用输出"No" 否则输出"Yes",并在第二行输出划分中的路径数
接下来 $ m $ 行每行两个整数 $ u_i,v_i $ 表示分解中的一条路径是从 $ u_i $ 到 $ v_i $ 的简单路径。 $ (1 \le u_i,v_i \le n,u_i \not= v_i) $
划分中的每一对路径都应该具有至少一个公共顶点，并且树的每一个边都应该在一个路径中呈现。
你可以按任意顺序输出路径。如果有多个分解，输出其中任意一个即可。
　
@来自洛谷U57304 jzzcjb

题解

• 以度数最大的点为根
• $ DFS $ 检查整张图是否形如以该点为中心的“菊花”
  　

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,in[100005],leaves[100005],comv[100005];
int main(){
	scanf("%d",&n);
	for(int u,v,i=1;i<n;++i){
		scanf("%d %d",&u,&v);
		++in[u]; ++in[v];
	}
	for(int i=1;i<=n;++i)
		if(in[i]==1) leaves[++leaves[0]]=i;
		else if(in[i]>2) comv[++comv[0]]=i;
	if(comv[0]>1){ puts("No"); return 0; }
	puts("Yes");
	if(!comv[0]) printf("1\n%d %d\n",leaves[1],leaves[2]);
	else{
		printf("%d\n",leaves[0]);
		for(int i=1;i<=leaves[0];++i) printf("%d %d\n",leaves[i],comv[1]);
	}
	return 0;
}/*
#        40052261
When     2018-07-07 08:55:52 
Who      PotremZ 
Problem  C - Useful Decomposition
Lang     GNU C++ 
Verdict  Accepted 
Time     62 ms 
Memory   1200 KB 
*/ 

codeforces CF981C Useful Decomposition 菊花图性质

标签：mon   描述   iostream   bit   puts   def   byte   接下来   输入输出   

原文地址：https://www.cnblogs.com/Potrem/p/CF981C.html