非递归 前序/中序/后序 遍历二叉树

 1 void preTraverse(const BiTree &T){
 2     //initialStack(stack)
 3     BiTree stack[MAX];
 4     int top=-1;
 5     BiTree p=T;
 6     //while(!stackEmpty(stack)||p)
 7     while(p||top>-1){
 8         while(p){
 9             //visit(p->data)
10             cout<<p->data<<" ";
11             //push(stack,p)
12             stack[++top]=p;
13             p=p->lChild;
14         }
15         //pop(stack,p)
16         p=stack[top--];
17         p=p->rChild;
18     }
19 }

 1 void inTraverse(const BiTree &T){
 2     //initialStack(stack)
 3     BiTree stack[MAX];
 4     int top=-1;
 5     BiTree p=T;
 6     //while(p||!stackEmpty(stack))
 7     while(p||top>-1){
 8         if(p){
 9             while(p){
10                 //push(stack,p)
11                 stack[++top]=p;
12                 p=p->lChild;
13             }
14         }else{
15             //pop(stack,p)
16             p=stack[top--];
17             //visit(p->data)
18             cout<<p->data<<" ";
19             p=p->rChild;
20         }
21     }
22 }

void postTraverse(const BiTree &T){
    stack<BiTree>s;
    BiTree p=T,prev=NULL;
    while(p||!s.empty()){
        while(p){
            s.push(p);
            p=p->lChild;
        }
        p=s.top();
        s.pop();
        if(p->rChild==NULL||p->rChild==prev){
            cout<<p->data<<" ";
            prev=p;
            p=NULL; 
        }else{
            s.push(p);
            p=p->rChild;
        }
    }
}

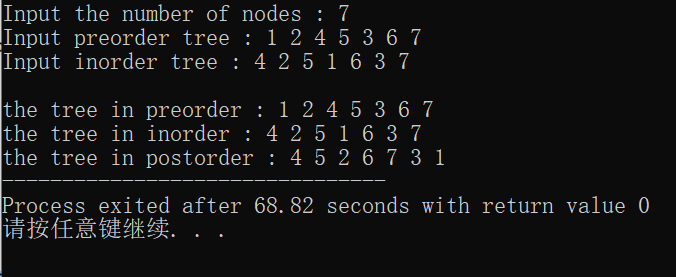
#include<iostream>
#include<stack>
#define MAX 100
using namespace std;

typedef struct BiTNode{
    public:
        int data;
        struct BiTNode *lChild,*rChild;
}BiTNode,*BiTree;

void preTraverse(const BiTree &T){
    //initialStack(stack)
    BiTree stack[MAX];
    int top=-1;
    BiTree p=T;
    //while(!stackEmpty(stack)||p)
    while(p||top>-1){
        while(p){
            //visit(p->data)
            cout<<p->data<<" ";
            //push(stack,p)
            stack[++top]=p;
            p=p->lChild;
        }
        //pop(stack,p)
        p=stack[top--];
        p=p->rChild;
    }
}

void inTraverse(const BiTree &T){
    BiTree stack[MAX];
    int top=-1;
    BiTree p=T;
    //while(p||!stackEmpty(stack))
    while(p||top>-1){
        if(p){
            while(p){
                //push(stack,p)
                stack[++top]=p;
                p=p->lChild;
            }
        }else{
            //pop(stack,p)
            p=stack[top--];
            //visit(p->data)
            cout<<p->data<<" ";
            p=p->rChild;
        }
    }
}

void postTraverse(const BiTree &T){
    //initialStack(stack)
    stack<BiTree>s;
    BiTree p=T,prev=NULL;
    while(p||!s.empty()){
        while(p){
            s.push(p);
            p=p->lChild;
        }
        p=s.top();
        s.pop();
        if(p->rChild==NULL||p->rChild==prev){
            cout<<p->data<<" ";
            prev=p;
            p=NULL; 
        }else{
            s.push(p);
            p=p->rChild;
        }
    }
}

bool preAndInCreate(BiTree &T,int pre[],int in[],int length){
    if(length<=0){
        T=NULL;
    }else{
        int i;
        T=new BiTNode; 
        T->data=pre[0];
        for(i=0;i<length&&in[i]!=pre[0];++i);
        if(i>length) return false;
        preAndInCreate(T->lChild,pre+1,in,i);
        preAndInCreate(T->rChild,pre+i+1,in+i+1,length-1-i);
    }
    return true;
}

bool deleteTree(BiTree &T){
    if(T){
        BiTree L=T->lChild;
        BiTree R=T->rChild;
        delete T;
        T=NULL;
        deleteTree(L);
        deleteTree(R);
    }
}

int main(){
    int n;
    cout<<"Input the number of nodes : ";
    cin>>n;
    cout<<"Input preorder tree : ";
    int pre[n],in[n];
    for(int i=0;i<n;++i) cin>>pre[i];
    cout<<"Input inorder tree : ";
    for(int i=0;i<n;++i) cin>>in[i];
    BiTree T=NULL;
    preAndInCreate(T,pre,in,n);
    cout<<"\nthe tree in preorder : ";
    preTraverse(T);
    cout<<"\nthe tree in inorder : ";
    inTraverse(T);
    cout<<"\nthe tree in postorder : ";
    postTraverse(T);
    deleteTree(T);
}