标签:线段 总结 数位 增加 大致 main 伪代码 就是 ace
考的是某年 \(FJWC\) 的题。
\(T1\) 比较简单的构造题,但自己考试的时候犯了个 \(zz\) 错误,把边权搞错了,就只拿了 \(50\) 分。
\(T2\) 大数据结构题,一开始想打暴力的,但要分类讨论好多种情况,就没写。
\(T3\) 思维题,打死都想不出正解的那照片那种。
你需要构造一棵至少有两个顶点的树,树上的每条边有一个非负整数边权。树上两点 \((i,j)\) 的距离 \(dis(i,j)\) 定义为树上连接 \(i\) 和 \(j\) 这两点的简单路径上的边权和。
我们定义这棵树的直径为,所有满足 \(1 \leq i < j \leq n\) 的 \((i,j)\) 中,\(dis(i,j)\) 最大的。如果有多个这样的 \((i,j)\),那么均为直径。
作为一个构造题,你需要构造一个恰有 \(k\) 个直径的树。可以证明在给定的限制下一定有解。
数据范围: \(2\leq n\leq 5000,1\leq k\leq 5\times 10^6\) 每条边的边权 \(0\leq w\leq 10^5\)
构造。
直径数为 \(a\times b\) 的构造方案很好想,只需要构造一个菊花图就可以了。
注意边权是可以等于 \(0\) 的,考虑如下图的构造方案:
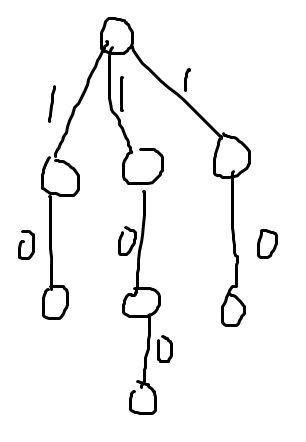
设三条链的长度分别为:\(a,b,c\) 那么直径数显然为:\(a\times b+b\times c+a\times c\) 。
暴力枚举 \(a,b,c\) ,在判断 \(a\times b+b\times c+a\times c\) 是否等于 \(k\) 即可。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
#define mp make_pair
const int maxn = 5000;
void print(int x,int y)
{
printf("%d\n",x+y+2);
printf("%d %d %d\n",x+y+1,x+y+2,2);
for(int i = 1; i <= x; i++) printf("%d %d %d\n",x+y+1,i,2);
for(int i = x+1; i <= x+y; i++) printf("%d %d %d\n",x+y+2,i,2);
}
void init(int x,int y,int z)
{
printf("%d\n",x+y+z+1);
printf("%d %d %d\n",1,2,1);
for(int i = 3; i <= x+1; i++) printf("%d %d %d\n",2,i,0);
printf("%d %d %d\n",1,x+2,1);
for(int i = x+3; i <= x+y+1; i++) printf("%d %d %d\n",x+2,i,0);
printf("%d %d %d\n",1,x+y+2,1);
for(int i = x+y+3; i <= x+y+z+1; i++) printf("%d %d %d\n",x+y+2,i,0);
}
int main()
{
freopen("diameter.in","r",stdin);
freopen("diameter.out","w",stdout);
int n; scanf("%d",&n);
for(int i = sqrt(n); i >= 1; i--)
{
if(n % i == 0)
{
if(i+n/i+2 <= maxn)
{
print(i,n/i);
return 0;
}
}
}
for(int i = 1; i <= 5000; i++)
{
for(int j = 1; j <= 5000; j++)
{
if(i*j > n) break;
for(int k = 1; i+j+k+1 <= 5000; k++)
{
if(i*j+i*k+j*k == n)
{
init(i,j,k);
return 0;
}
else if(i*j+i*k+j*k > n) break;
}
}
}
fclose(stdin); fclose(stdout);
return 0;
}
作为 ByteLand 中最出色的开发者,你刚刚开发了一款新游戏。
为了赚更多的钱,这个游戏的主线剧情分为 \(n\) 个 DLC 出售。你打算发行 \(n\) 种预购套装,第 \(i\)
\((1 ≤ i ≤ n)\) 种套装包含前 \(i\) 个 DLC。当然,第 \(i\) \((2 \leq i \leq n)\)个套装的价格需要严格高于第 \(i?1\) 个套
装的价格,并且第 \(1\) 个套装的价格大于 \(0\)。现在你需要确定这 \(n\) 个价格。
在 Byteland,所有物品的价格都只能为 \(m\) 位二进制非负整数。此外,政府限制了每个价格的某些
二进制位必须为 \(0\)。为了体现你是良心开发商,你需要求出所有 套装 的价格和的最小值。由于这个值可
能太大了,你只需要输出它 \(\mod 10 9 + 7\) 后在十进制下的值。
天有不测风云,政策瞬息万变。一开始政府限制了每个价格的每个二进制位都必须为 \(0\),后来随着
时间推移,政府可能会允许某个价格的某个二进制位可以为 \(1\),或重新限制某个二进制位必须为 \(0\),你
必须高效地对政策的变化作出反应,并随时支持求出价格和的最小值。
数据范围:\(1\leq n\leq 1000,1\leq m\leq 10^9,1\leq q\leq 500000\), 操作 \(2\) 的数量不超过 \(1000\)。
贪心+单调栈+set。
不会做,直接搬题解。
显然定价正确策略就是贪心确定每个产品的价格。
观察数据范围可以发现我们大概是需要在 \(O(nlogn)\) 的时间内模拟这个贪心。
我们先总结一下贪心的时候在干啥。
假设我们上一行有若干位为 \(1\),那么对于下一行,我们需要找到最高的为 \(1\) 位,满足这一行这位不能再为 \(1\) 了,我们就需要选取在这个位置之前的一个可以变成 \(1\) 的 \(0\) ,把它变成 \(1\),并把后面的位置全变成 \(0\)。直接用 \(bitset\) 维护可以获得部分分。
我们考虑使用一个栈维护当前的 \(1\),假设我们能找到最高的不能继续为 \(1\) 的位,我们就可以从这一位开始依次遍历前面的 \(1\),找到这个 \(1\) 之前第一个可以变成 \(1\) 的位置,如果这个位置在下一个 \(1\) 之前就是答案。
考虑如何找到最高的不能继续为 \(1\) 的位。对于栈内的每个元素,我们算出它到哪一行时不能继续为 \(1\),我们对于这些行维护一个优先队列,出栈时也在优先队列里弹出,这样就可以查询出所有不能继续为 \(1\) 的位了。
由于每次 \(1\) 的个数只会增加 \(1\),这样均摊复杂度就是对的了。
算到哪一行时不能继续为 \(1\) 和找到每一行某一个位置前的第一个能为 \(1\) 的位置可以使用你喜爱的数据结构维护,例如动态开点线段树,set<pair<int,int>>等。
zzq 近日发明了一种最新的排序算法 FastSort,它的伪代码大致如下:
function FastSort(a, n)
cnt ← 0
for i ← 1 to n do
for j ← i + 1 to n do
if a j < a i then
tmp ← a j
a j ← a i
a i ← tmp
end if
cnt ← cnt + 1
end for
end for
return a
end function
当然,这个伪代码里的 \(cnt\) 对排序来说没什么用,它只是用来指示这个算法的运行效果的。
zzq 很喜欢这个算法,于是他打算用它来给一个 \(1,2...n\) 的排列 \(a\) 排序。为了清楚地获取算法的运
行过程,zzq 决定在每次 \(cnt\) 改变时记录下当前的 \(cnt\) 和 \(a\) 便于分析。
zzq 运行了这个算法之后就睡觉去了。第二天早上,zzq 发现昨天停电了,日志里只剩下了记录下的
最后一个 \(cnt\) 和 \(a\)。zzq 不想再运行一遍算法了,于是他想让你确认一下记录是否正确。
一句话题意:对给定的 \(1,2...n\) 的排列 \(a\) 执行算法 FastSort,问当 \(cnt\) 刚刚变成输入中给定的值
时的 \(a\) 序列。
数据范围:\(2\leq n\leq 10^6,1\leq cnt\leq {n(n-1)\over 2}\)
打表找规律+模拟。
正解的话太过神仙了,没有看懂。
找了一篇找规律的题,发现其实挺好写的。
考虑先算出外层进行完第 \(k\) 轮每个数的位置,然后在暴力模拟剩下的步数即可。
打表找一下每个数位置的规律:
//第一轮:1 9 5 4 8 7 2 3 6
//第二轮:1 2 9 5 8 7 4 3 6
//第三轮:1 2 3 9 8 7 5 4 6
//第四轮:1 2 3 4 9 8 7 5 6
//第五轮:1 2 3 4 5 9 8 7 6
//第六轮:1 2 3 4 5 6 9 8 7
//第七轮:1 2 3 4 5 6 7 9 8
//第八轮:1 2 3 4 5 6 7 8 9
//第九轮:1 2 3 4 5 6 7 8 9
可以发现一个规律:设原序列中第 \(i\) 个数前面比 \(a_i\) 大的数有 \(num_i\) 个,则 \(a_i\) 在前 \(num_i\) 轮的位置保持不动,在第 \(num_i+1\sim a_i\) 轮,\(a_i\) 逐个变到原序列中他后面比她小的数的位置,第 \(a_i\) 轮回到第 \(a_i\) 个位置。
有了这个规律之后,随便拿个数据结构(线段树/单调栈)维护一下即可。
标签:线段 总结 数位 增加 大致 main 伪代码 就是 ace
原文地址:https://www.cnblogs.com/genshy/p/14603577.html