标签:开头 相对 uid pair math 中心 卡尔 特性 spl
OpenFOAM 自带的壁面函数边界条件可以分别用于不同边界面33。不同的壁面可以使用不同的壁面边界条件。我们可以对湍流粘度场????内进行修改以使用不同壁面函数,其位于0/nut 文件夹内。
在这个算例中,通过把movingWall 和fixedWall 指定为nutWallFunction 类型来使用标准壁面函数模型。其它的壁面边界模型,例如粗糙壁面边界类型,可以通过nutRoughWallFunction关键词来指定。
??为epsilonWallFunction 边界条件,k 为kqRwallFunction 边界条件。后者是一个普适性边界条件,它可以用于任何的湍动能类场,例如k、q、以及雷诺应力R 场。最初的k 和??值通过对速度波动量,??′,和湍流尺度量,????,进行预估来计算,k 和??的计算公式如下:
其中,????是?? ? ??模型的标准参数,其值为0.09。对于笛卡尔坐标体系,k 的计算公式为:
其中,???? ′ 2,???? ′ 2,???? ′2是速度在??,??,??方向的脉动速度。
在求解器最开始运行的时候,它会读取tubulenceProperties 字典文件里面的simulationType 关键词来获取湍流模型的相关信息。
可选的simulationType 有laminar,RAS 以及LES
kEpsilon对应的是标准?? ? ??模型;同时,用户应该确保turbulence 设置为on 的状态。
每个湍流模型的参数都存储在每个湍流模型的代码中并且具有一个默认值。printCoeffs开关如果设置为on 的话,这些参数的值会被输出到终端。它们以子字典的形式被输出,我们会看到每个模型的名字后面都加上了Coeffs,例如kEpsilon 模型会输出kEpsilonCoeffs。这些模型的参数也可以通过在RAS 子字典文件中自定义来修改。
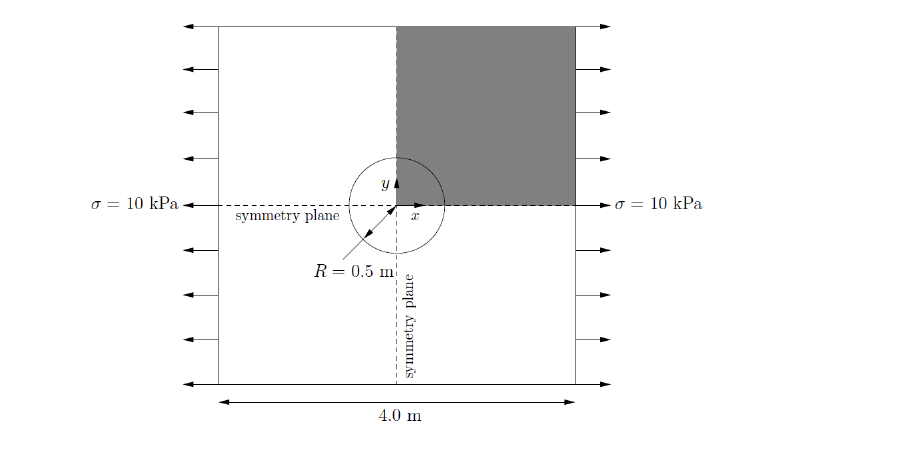
由于负载被附加于盘体的一个平面上,因此这个问题可以看做是二维的。在笛卡尔坐标系下面,关于第三个维度的行为存在两种假定:
(1)应力平面条件:适用于在这个2D 平面外的第三维度的应力是可忽略的情况;
(2)应变平面条件:适用于在这个2D 平面外的第三维度的应变是可忽略的情况。
应力平面条件对于那些第三维度方向非常薄的算例是合适的。应变平面条件对于第三维方向比较厚的情况下适用。
对于一个无限大的中心带有圆形空洞的薄盘,它存在解析解。垂直于应力对称平面的解析解为:
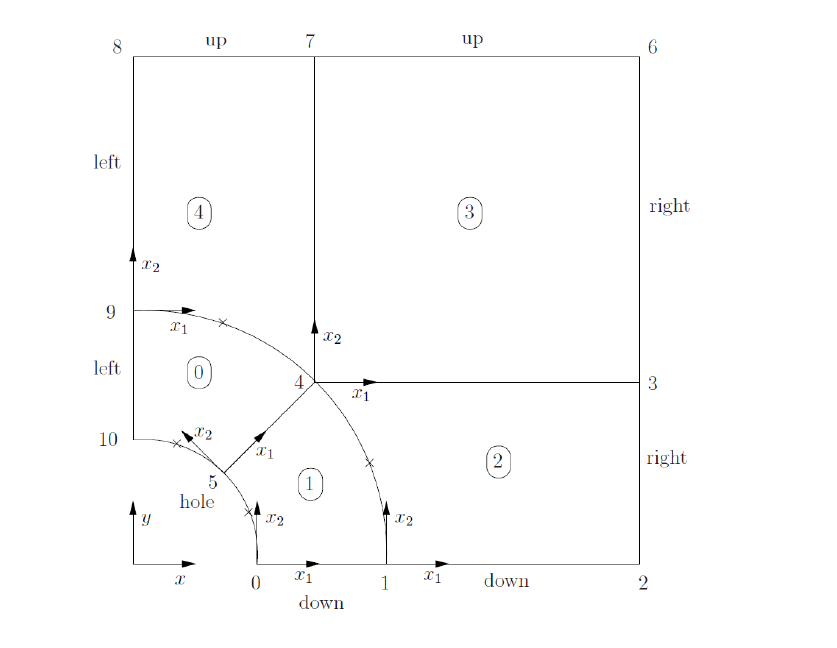
制作曲边block,可以通过修改关键词edges下的相关信息来完成。
Edge 下面的语句要确保每行信息以arc,simpleSpline,polyLine 等开头
在这个例子中,所有的曲边都是圆形的,因此可以用arc 关键词来指定。后面的信息是弧边的起始点和终止点的标示,以及这个弧边通过的点的坐标。
patch 如下定义:
平板的每个边为一个patch,空洞为一个patch,前后面各为一个patch。左边和下面的patch 是对称面。这个对称面是一个几何的对称面。因此它需要在网格里面进行定义而不是简单的定义一个初始边界条件。用户需要在blockMeshDict 里面使用symmetryPlane 关键词来定义。
frontAndBack,这个patch 代表了这是一个2D 的算例,在计算中这个patch 将被忽略。再次提醒一下,这是一个几何方面的限制,因此需要在网格内进行定义。用户需要在blockMeshDict 中将其定义为empty。
一旦网格生成后,必须指定边界条件的初始场。
patches 是应力边界条件,应力边界条件通过traction 字符来指定。它由以下两个关键词组合来构成:
(1)在关键词traction 下指定应力边界矢量和大小。
(2)在pressure 关键词下,如果这个边界面法向应力指向表面之外,就被定义为负值。
在物理特性字典中,需要指定planeStress为yes。
稳态问题,因此用户应该在timeScheme 的时间离散里面选择SteadyState。这就屏蔽掉了时间离散项。
在流体力学中,并不是所有的求解器,可以即用稳态又用瞬态来进行计算。但是solidDisplacementFoam可以计算稳态又计算瞬态,因为对于这个求解器,两种类型的算法大体相同。
最小二乘法 计算梯度的least squares 对网格较差的算例较好
应力分析的动量方程包含几个含有位移梯度量的显性项。梯度项计算的精准性和光滑性对结果有很大影响。一般情况下,有限体积离散建立于高斯定律之上,高斯定律对于大部分的模拟目的来说是足够精准的。
控制求解线性方程组使用的矩阵求解器
D 的矩阵求解器为GAMG。求解器的tolerance 是。矩阵求解器的相对误差由relTol 控制,控制每次迭代的残差减小量。本例中设置一个很小的残差是不经济的,因为方程组中很多项是显性的,并且采用分离迭代求解技术。因此,合理的迭代残差为0.01,更高也是可以的,比如0.1,在某些例子中,0.9 也是可以的
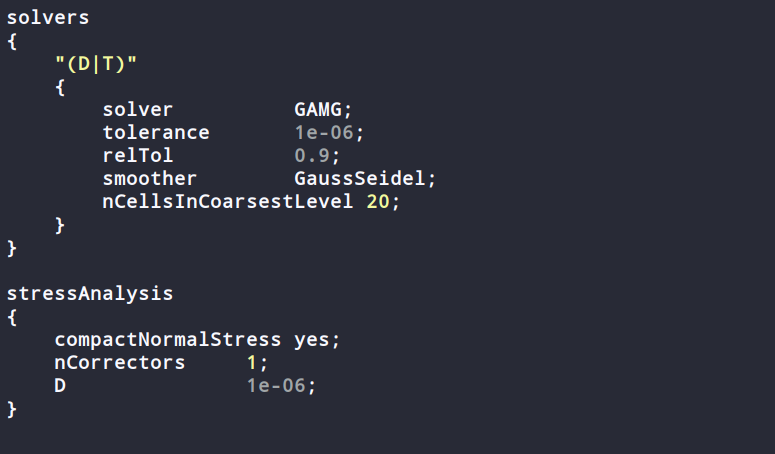
包含了这个求解器所需的控制参数
nCorrectors 表示整个方程组求解的外循环数,包括每个时间步的拉伸边界条件。
由于这是一个稳态问题,我们用时间步代表迭代数。因此我们可以设置nCorrectors 为1。
关键词 D 指定外循环的收敛残差,例如:设置一个残差,当达到这个值的时候迭代停止。这个残差,本例为,应该在运行之前就设定好。
postProcess -func “components(sigma)”
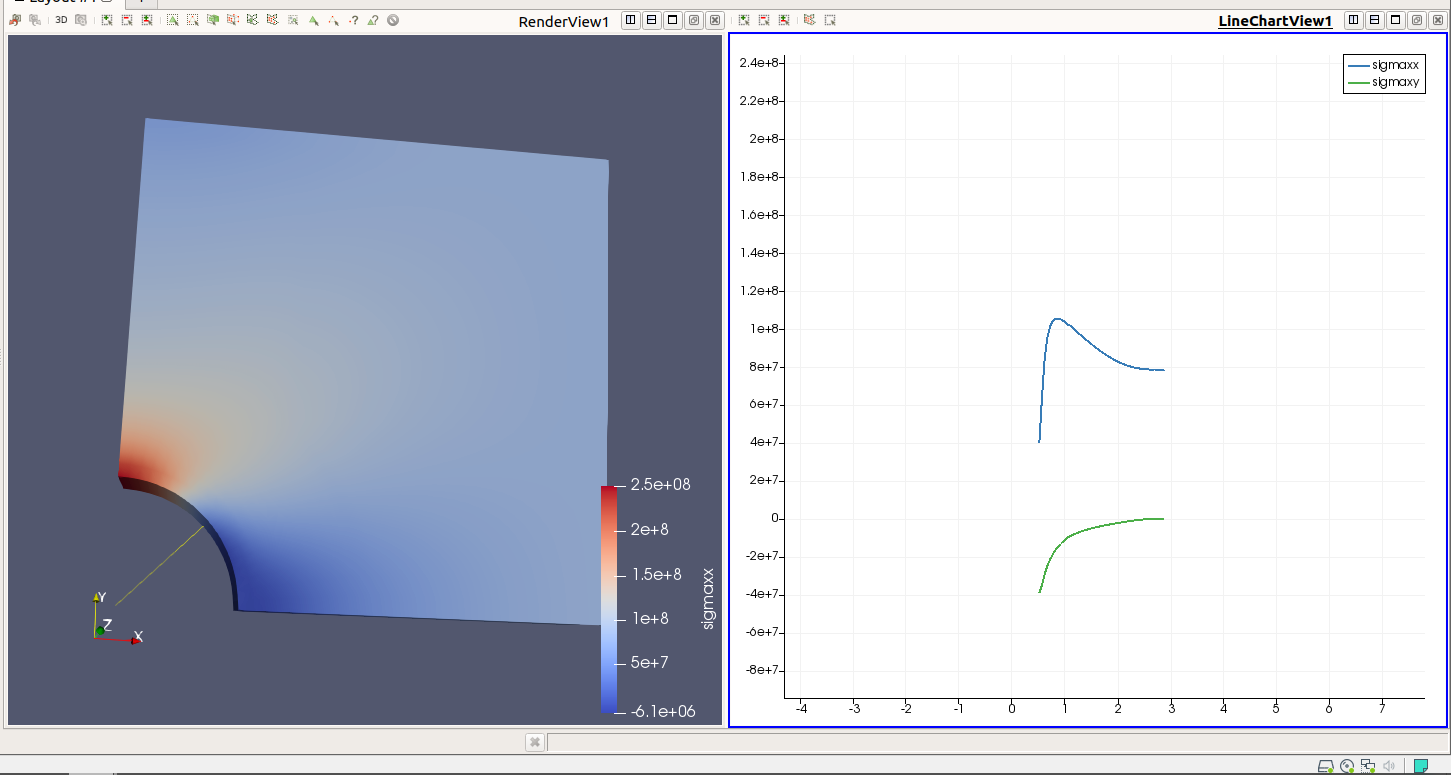
singleGraph 数据输出
需要提供postProcess读取的字典文件
postProcess -func “singleGraph”
其写入格式为raw,并提取出2 列的原始数据。
数据随后被写入postProcessing/singleGraph下的每个时间步文件中。例如:100s 的场数据存储在singleGraph/100/leftPatch_sigmaxx.xy中。
依靠GnuPlot,用户可以使用如下命令来把精确解和数值解画在同一个图中:
plot [0.5:2] [0:] ‘postProcessing/sets/100/leftPatch sigmaxx.xy‘,1e4*(1+(0.125/(x**2))+(0.09375/(x**4)))
标签:开头 相对 uid pair math 中心 卡尔 特性 spl
原文地址:https://www.cnblogs.com/Augustusben/p/14608306.html