康威生命游戏的简要介绍, 实际上这并不是传统意义上的游戏, 而是一种数学模型, 通过简单的规则, 模拟出生命的繁衍和演化.
有限状态自动机 (Finite-state Machine), 简称自动机, 是一种对有限状态之间转移的数学模型. 这里的自动机范围很广, 简单到处理逻辑运算的晶体管, 复杂到处理多模式串匹配的 AC 自动机, 都是自动机的应用实例. 晶体管源极接受一个源电压, 这是状态, 根据栅极电压的有无, 即条件, 最后在漏极的漏电流有无就是转移. AC 自动机中, 字符串中已经匹配的模式串的公共子串就是状态, 正在判断的这个字符就是条件, 自动机跳 Fail 边或沿着 Tire 的边往下走都是转移, 无论失配还是成功匹配, 新的匹配的子串就是转移后的状态.
由美国数学家冯·诺依曼于 \(20\) 世纪 \(50\) 年代提出, 又称细胞自动机. 一个任意维的空间, 由无限个相同的单元组成, 每个单元有有限种状态, 状态转移的规则和它的邻域中的单元状态有关.
每个单元的邻域是与它相邻的单元集合, 相邻的定义对于任意单元都相同, 而且任意单元邻域有限. 因为邻域是单元集合, 所以一个单元邻域中单元和它本身的相对位置不影响集合的组成.
元胞自动机的规则是将一个单元的状态, 通过邻域中的单元状态集合为条件, 转移到另一种状态的规则.
在状态转移时, 每个单元读取邻域单元当前阶段的状态用来转移, 所有单元同时进行转移.
康威生命游戏, 是由英国数学约翰·康威于 \(1970\) 年提出一种元胞自动机, 简称生命游戏. 一个二维的网格, 每个格子是一个单元, 有 \(0\), \(1\) 两种状态, 表示有无生命. 单元邻域是它周围的八个格子, 即和它八连通的格子. 一个阶段在生命游戏中被认为是一代. 生命游戏的规则不是固定不变的, 但是一般它的规则是这样的.
生命害怕孤独, 当一个格子有生命, 且其邻域中生命数量小于 \(2\) 时, 它会孤独而死.
生命有生存竞争, 当一个格子有生命, 且其邻域中生命数量大于 \(3\) 时, 它会拥挤而死.
生命有繁殖能力, 当一个格子无生命, 且其邻域中生命数量大于等于 \(3\) 时, 这个格子会产生生命.
其余情况下, 格子状态保持不变
我们把这种规则称为 B3/S23, B 指 Being, 即存在生命, S 指 Stay, 即保持原来状态不变. 字母后面的每个数字都是执行字母代表的转移的条件, 即邻域生命数量. 在 B 和 S 的条件同时满足时, 优先按 B 转移.
由于每个单元的影响范围有限, 所以和外界互不影响的单元集合称种群. 显然, 一个种群和其他种群在同一世界的发展和这个种群单独在一个世界中发展的本阶段的结果是一样的.
之后提到状态一般指一个种群的状态. 种群的稳定状态指在没有外界干扰的情况下, 无论过多少代, 这个种群保持此状态不变, 简称稳态.
最简单的稳态是一个 \(2*2\) 的正方形 (A 表示 Alive, 即存在生命; D 表示 Dead, 即不存在生命)
状态如图

四个生命的邻域中都有三个生命, 所以都保持存在生命, 周围的格子邻域中的生命都小于 \(3\), 不会生成新生命.
与稳态不同的是, 这种状态的种群在经历一系列变化后会回到初始状态. 显然, 回到原始状态后它会再次经历一次这杨的变化, 陷入一个无限的循环. 从一个状态开始回到这个状态所经历的阶段数就是这个循环的周期. 我们吧这种状态称为振荡状态, 简称振荡.
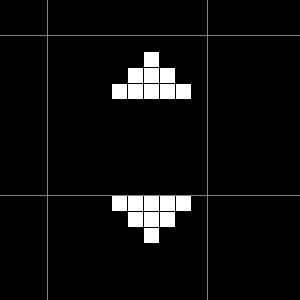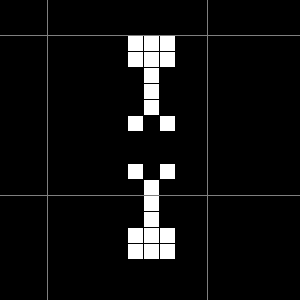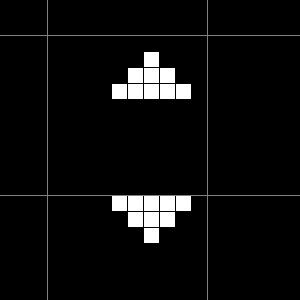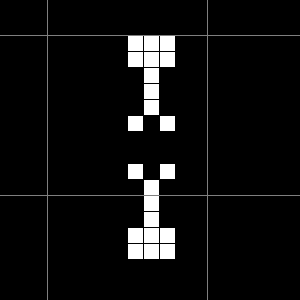
图中是一个振荡, 周期为 \(15\), 名为十五项全能
是震荡状态的变种, 每个周期种群移动一定距离, 这就是飞船.
图中是最简单的飞船, 周期为 \(4\), 名为滑翔机 (Glider).

生命游戏是计算机科学, 数学的结合, 它在某种程度上模拟了生命的演变, 在接下来的学习中, 我们还能领略到其中递归的思想和无限增值, 人们甚至可以在生命游戏中制造计算机并且证明了它的图灵完备性. 而这一切, 都是前面提到的简单得不能再简单的基本规则支配的, 正如现实世界中的万物都要遵循最基本的力学定律一样.
原文地址:https://www.cnblogs.com/Wild-Donkey/p/14614483.html