二分图

标签：alt   scanf   inf   放弃   思路   二分   pre   集合点   枚举   

二分图就是可以把所有点划分到两边去，使得所有边都是在集合之间的，而集合内部没有边。如下图：

1.1 染色法

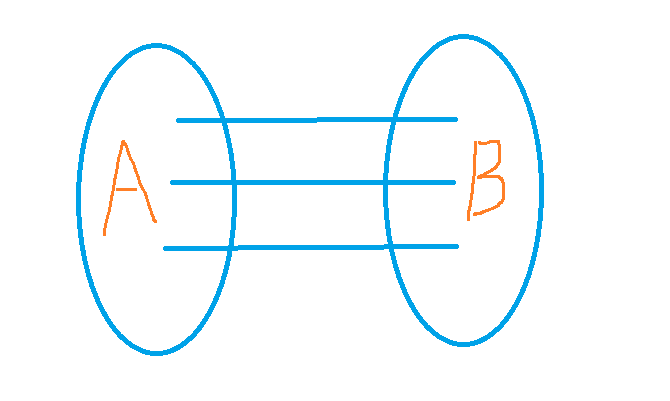
时间复杂度：O(n+m)

用来判断一个图是不是二分图。染色法就是一个很简单的DFS。

图论的一个性质：一个图是二分图，当且仅当这个图可以被染色。

一个图是二分图，当且仅当图中不含奇数环。环是从一个点出发可以回到自己的路径。奇数环就是这个环中边数是奇数。

对应于二分图定义，一个环如果是奇数环，那么如下图：

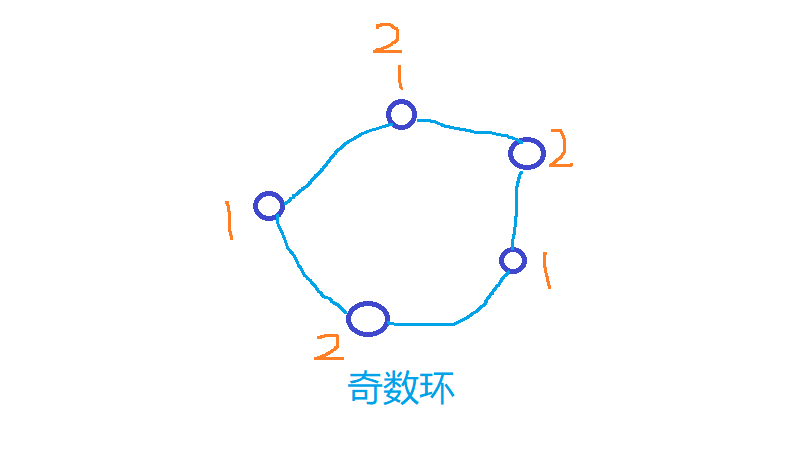
初始点既是第一个集合又是第二个集合的，矛盾。

框架：

for(int i = 1; i <= n; i++){

? if i未染色：

? dfs(i); // 把i所在的连通块整个染一遍

}

1.2 练手：染色法判断二分图

1.3 解答：染色法

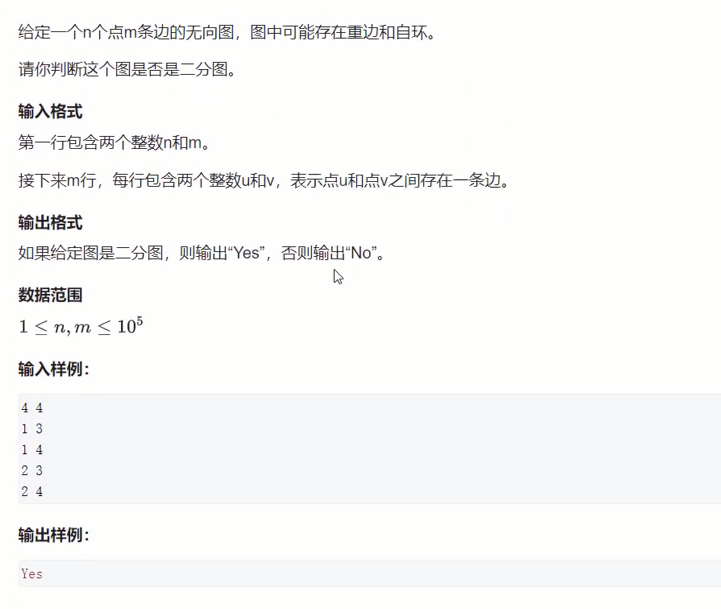
可以搜索关押罪犯这道题，都是染色法。

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010, M = 200010;

int n, m;
int h[N], e[M], ne[M], idx;
int color[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool dfs(int u, int c)
{
    color[u] = c; // 记录当前点颜色是c

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i]; // 存储当前点的编号
        if (!color[j]) // 没染色，就染成另一种颜色，3-c把变成2，2->1
        {
            if (!dfs(j, 3 - c)) return false;
        } // 端点两边颜色相等，矛盾了
        else if (color[j] == c) return false;
    }

    return true;
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }

    bool flag = true; // 表示染色时候是否有矛盾发生
    for (int i = 1; i <= n; i ++ )
        if (!color[i]) // 如果当前点没被染过色
        {
            if (!dfs(i, 1))
            {
                flag = false;
                break;
            }
        }

    if (flag) puts("Yes");
    else puts("No");

    return 0;
}

1.4 匈牙利算法

时间复杂度：O(mn)，但实际运行时间一般远小于O(mn)。

n是点的数量，m是边。

求二分图的最大匹配。

基本思路：可以在比较快的时间内告诉我们，左边和右边匹配成功的最大的数量是多少。

匹配成功指：不存在两条边共用一个点。

初始状态如下：

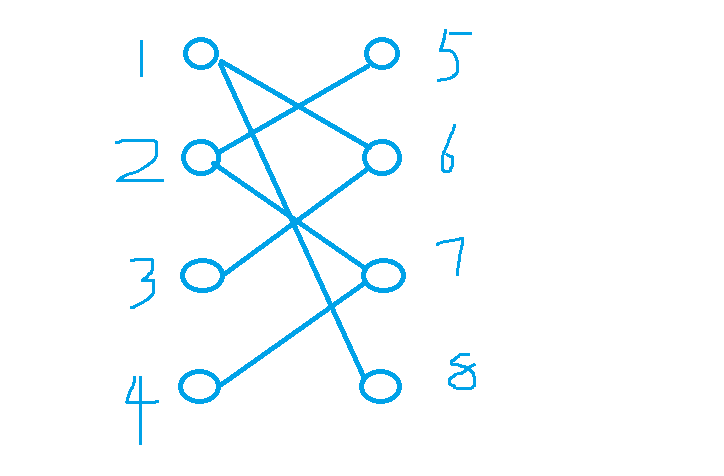
两两开始匹配，匹配到3号点时：

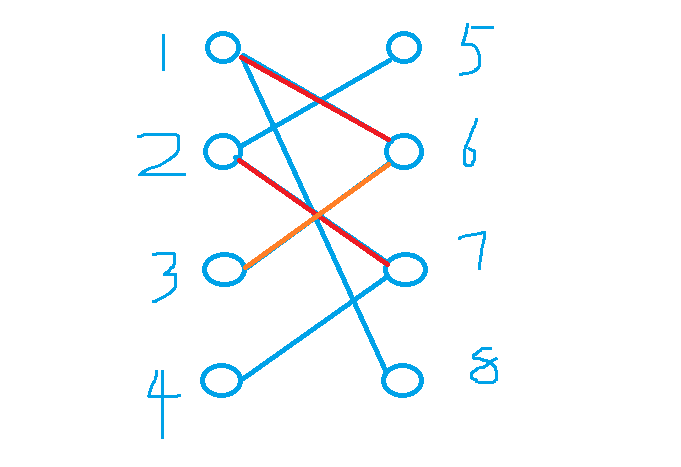
3号点只有一个选择可以连接，匈牙利算法中3号点不撞南墙不回头，他会继续尝试，但因为不能有两条边共用一个点，所以就要看1号点，发现1号点还可以连接8号点，那么1号点就改为连接8号点。

每次匹配时，如果当前匹配的点已经有人连接了如1，6，那么就要看看1有没有其他点可以选择，如果有就匹配其他点，如果不能那么就只能放弃了。

最后结果如下：

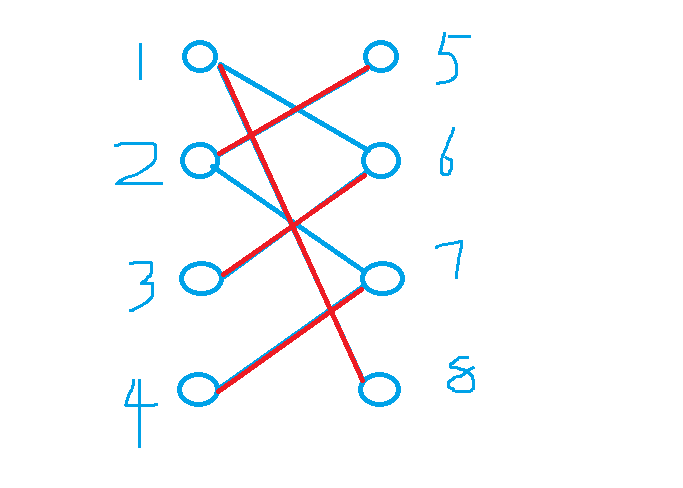
最终匹配数量为4。

1.5 练手：

2.6 解答：

// 把左面部分看成男生，右面看成妹子
// 可以看一下棋盘覆盖这道题
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510, M = 100010;

int n1, n2, m;
// 如果数组越界了，即开小了，什么错误都可能发生
int h[N], e[M], ne[M], idx;
int match[N]; // 记录右边的点与左边哪些点有边相连
bool st[N]; // 判重，不要重复搜索一个点

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool find(int x)
{
    // 枚举左面所有点看上的右面的点的集合
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i]; // 当前集合点的编号
        if (!st[j]) // 右面这个点之前没考虑过
        {
            st[j] = true;
            // 如果这个妹子还没有匹配任何男生 或
            // 虽然匹配了男生，但是我们可以为这个男生找到下家，
            // 这个妹子就可以匹配当前男生了
            if (match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }

    return false;
}

int main()
{
    scanf("%d%d%d", &n1, &n2, &m);

    memset(h, -1, sizeof h);

    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }

    int res = 0; // 匹配数量
    // 从上到下依次分析左面每个点要对应右面哪个点
    for (int i = 1; i <= n1; i ++ )
    {
        // 先将右面每个点清空，表示还没有匹配过
        memset(st, false, sizeof st);
        if (find(i)) res ++ ;
    }

    printf("%d\n", res);

    return 0;
}

二分图

标签：alt   scanf   inf   放弃   思路   二分   pre   集合点   枚举   

原文地址：https://www.cnblogs.com/ApStar/p/14616068.html