标签:否则 反射 异或 大于 对比 att 重要 原理图 struct
类似于双目,如果把投影仪看成一个逆相机,直到空间中的一点成像平面的位置,就可以知道空间中一点的坐标。
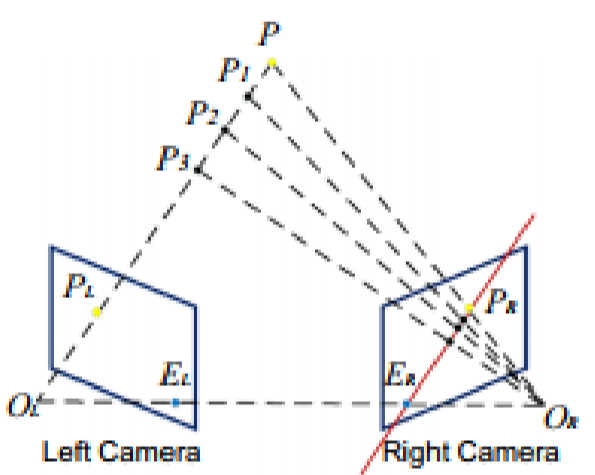
编码的目的:知道打在物体物体表面的光是从投影仪的那个像素发出来的,就知道在投影仪的虚拟成像位置。
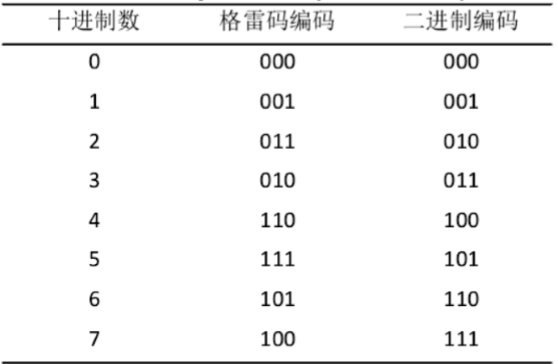
格雷码是一种二进制码,最大的特点是相邻格雷码编码只有一位不同。
所以格雷码解码更稳定,相对不容易出错。
体现在
对于格雷码来说,明暗交接处变换更少,如图所示二进制下部有7次变换,而格雷码只有4次。黑白交接的影响主要是在解码上,解码很重要的环节就是二值化,一般情况下全黑和全亮是不容易出错的,因为在实际应用中投影交界处是渐变的,阈值很难确定(还有物体边缘的影响)。
在相机对焦外,可能投影会糊掉,所以条纹越宽越不容易糊掉。
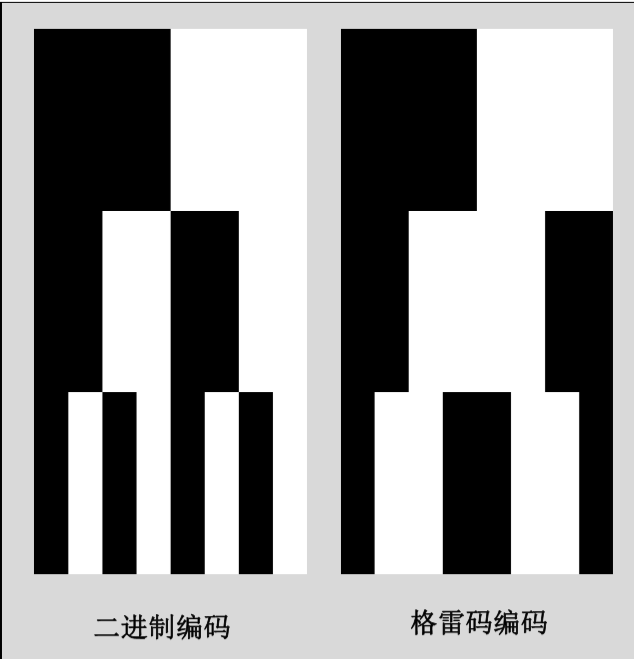
如果单纯的编制一张图片的话很简单,如上一节图所示,最低一行(最后一位)变化为0110周期,第二行为0011100周期,第三行为0000111111110000周期(2的指数级增长)。
二进制码->格雷码
1.对n位二进制的码字,从右到左,以0到 n-1编号
2.如果二进制码字的第i位和i+1位相同,则对应的格雷码的第i位为0,否则为1
格雷码->二进制码
从左边第二位起,将每位与左边一位解码后的值异或,作为该位解码后的值(最左边一位依然不变)。依次异或,直到最低位。依次异或转换后的值就是格雷码转换 后的二进制值。
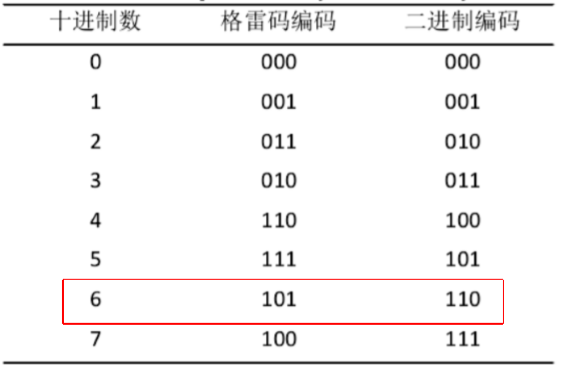
以十进制数6为例,格雷码->二进制码
第一位不变: 1
第二位(0)与第一位解码后的值(1)异或:1
第三位(1)与第二位解码后的值(1)异或:0

前提条件:每个在投影仪照射范围的点都至少需要经历一次明暗变换,即总要能找到一张图该位置为 0,另一张图该位置是1
实现方法:
方法一: 增加两张图, 一张全黑图,一张全亮图
方法二: 去除全0和全1的编码 ,让每个编码至少含有一个0和一个1(不建议,可能会破坏格雷码稳定性)
二值化方法:
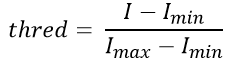
对于每个像素,计算其在整个时间序列(一组)下的最大值和最小值,然后对当前图片像素二值化就 是计算出一个如上式所示的阈值,阈值大于0.5的时候则为1,小于0.5则为0。
在某些场景下,由于物体材质的原因,格雷码效果不好;物体受到全局光照影响特别大;
Global illumination 全局光照:
1 inter-reflection 内反射 -- long range effect
2 diffusion 漫反射 – long range effect
3 sub-surface scatter 下表面散射 – short range effect
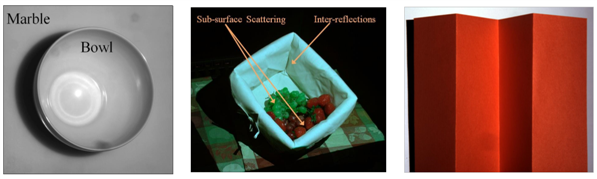
全局光照对解码影响:解码错误
解决思路:
不同的全局光,对不同频率的编码光影响不同。
1 高频光适合 (long range effect): 内反射, 漫反射
有可能第一行右边亮的地方点亮左边暗的地方,所以需要更密集的投射如下:
2 低频光适合 (short range effect): 下表面反射(影响临近的点)
低频光因为影响临近,所以最好是越低频越好,如下:

其实相对来说格雷码最稳定,而上面这种方法会生成过多的图片,会对点云帧率有所影响。

参考论文: Structured Light 3D Scanning in the Presence of Global Illumination
格雷码编解码流程:

特殊应用场景:


标签:否则 反射 异或 大于 对比 att 重要 原理图 struct
原文地址:https://www.cnblogs.com/sabai/p/14626150.html