标签:括号 ima 没有 image 特殊 最简 font form 包含
这节课的目的是找出行列式的公式
推导思路:
首先我们从二阶行列式开始
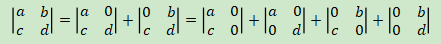
有上一节关于对角矩阵的性质,我们可以得出上面最右边式子的值为0+ad-bc+0=ad-bc;
我们推广到三阶行列式,有27(n!个)个行列式相加| |+| |+| |+...
我们都写出来未必太麻烦了,我们试图从二阶行列式中找出规律,规律应该是每一行取一个元素,且这些元素不在同一列,最后他们的乘积相加(或相减,这里不做讨论,只找出思路)
再推广到n阶
我们得出一个BIG FORMULA(大公式)
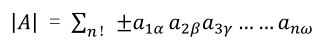
我们还可以以此公式反推出行列式的性质,比如性质一,只有主对角线各元素乘积中没有零,比如性质十,因为是方阵,所以横着取个元素的排列组合,和竖着取是完全一样的。(因为这些元素即不在同一行,也不在同一列)。
接下来引入求解行列式的另一种方法-通过代数余子式
我们把大公式的公因式提取,对应的括号内的因子其实就是代数余子式的绝对值,要想获取符号,得跟踪因子中的某一项的正负,其实代数余子式就是把第一行选的元素所在的行和列去掉,然后
从剩余n-1行和n-1列选取,那么这n-1行和n-1列中的元素构成一个n-1阶行列式,这就是代数余子式,不包含正负符号的代数余子式称为余子式
接着教授给出了代数余子式的正式定义Cij为aij的代数余子式。一个行列式可以分解为第一行中每个元素乘以对应的代数余子式然后加和。
但是以上两种方法求解行列式的值都没有用上一节讲的性质算行列式简单,即最简单的方式是通过性质五化为阶梯形矩阵,然后根据性质七对角线元素相乘得到。
最后,教授讲了一个非常特殊的矩阵,三对角线矩阵,并通过按行展开方式复习一遍按行展开求行列式的方法。
标签:括号 ima 没有 image 特殊 最简 font form 包含
原文地址:https://www.cnblogs.com/cllcharge/p/14639287.html