标签:位置 code efi 下标 直接 应该 pre add 顺序
本篇文章只对奇数阶以及偶数阶中阶数n = 4K的魔方阵进行讨论.下面就让我们进入正题:
1 :魔方阵的相关信息:(百度百科)
https://baike.baidu.com/item/%E9%AD%94%E6%96%B9%E9%98%B5/10973743?fr=aladdin
2 :奇数阶和偶数阶魔方阵的排列规律.(源自百度百科) (可跳至第三部分)
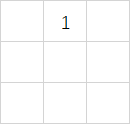 ,
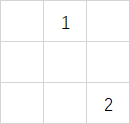
,
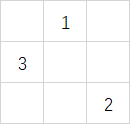 ,
,#include<assert.h> #include<stdio.h> void Magic_Square_1() { #define ROW 3 #define COL ROW // 等价于 #define COL 3 assert(ROW % 2 != 0); if (ROW % 2 == 0)//ROW & ! == 1 判断是否为奇数 &(只有全为1,才为1) { return; } int preRow = 0; //记录上一个数的行坐标 int preCol = 0; //记录上一个数的列坐标 int ar[ROW][COL] = {}; ar[0][COL / 2] = 1; //先放1 preRow = 0; preCol = COL / 2; for (int i = 2; i <= ROW * COL; i++)//1已经放入所以从2开始进行 { if (ar[(preRow - 1 + ROW) % ROW][(preCol + 1) % COL] == 0) //判断上一个数的上一行下一列是否有值若没有则放入当前的i { preRow = (preRow - 1 + ROW) % ROW; preCol = (preCol + 1) % COL; } else { // 若有则i放在上一个数的下一行. preRow = (preRow + 1) % ROW; } ar[preRow][preCol] = i; } for (int i = 0; i < ROW; i++)//打印 { for (int j = 0; j < COL; j++) { printf("%3d", ar[i][j]); } printf("\n"); } #undef ROW //取消定义 #undef COL }
int main()
{
Maagic_Square_1();
return 0;
}
运行结果:

3.2.2) : 将取出来的值按照从大到小的顺序(或从小到大的顺序)排好,从二维数组的[0][0]下标开始(从二维数组[ROW - 1][COL - 1]的位置开始) 依次填入到数组中空白的位置.
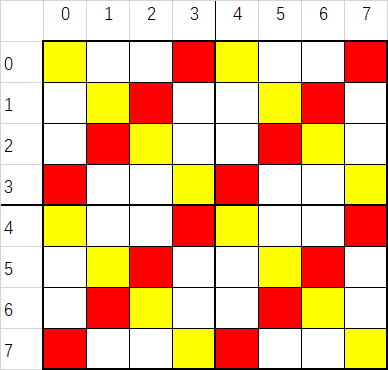
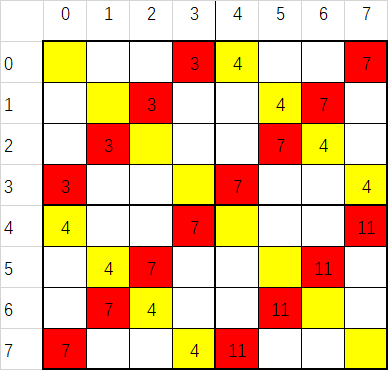
(重点)排列n= 4*k 阶的魔方阵的关键是取出各个四阶魔方阵的对角线的元素.我们可以发现:所有在对角线的元素的行列下标只差都满足一定的规律:
即 |row - col|(绝对值) % 4 == 0 (对应图中黄色部分)或者(row + col)%4 == 3(对应图中红色部分) .同时我们可以定义一个数组br[ROW*ROW/2],
在第一步填入数据时对其行列下标进行判断,若满足对角线元素下标的特点,直接将数值存放到br中,同时对二维数组相应的位置赋零值.
这样br 中的数就是从小到大排列的,只需要在第二步时从二维数组ar 的ar[ROW - 1][COL - 1]的位置开始,
依次将数组br中的值填入到数组中空白的位置.
代码如下:
#include<stdio.h> #include<assert.h> void Magic_Square_4K() { #define ROW 8 #define COL ROW int ar[ROW][COL] = {}; int br[ROW*ROW/2] = {};//用来存储4阶方阵对角线元素. int num = 1;//从1开始填入 int k = 0;//数组br下标. for (int i = 0; i < ROW; i++) { for (int j = 0; j < COL; j++) { if((i-j)%4==3||(i-j)%4==0|| (j - i) % 4 == 3 || (j - i) % 4 == 0) {//先控制对角线元素为零,并将应该填在对角线的这些数记录到br中. br[k] = num; k += 1; ar[i][j] = 0; } else { ar[i][j] = num; } num++; } } int tag = 0; for (int i = ROW - 1; i >= 0; i--)//将br中的数按照顺序,从ar[ROW-1][COl-1]开始对ar中为零的元素赋值. { for (int j = COL - 1; j >= 0; j--) { if (ar[i][j] == 0) { ar[i][j] = br[tag]; tag += 1; } } } for (int i = 0; i < ROW; i++)//打印 { for (int j = 0; j < COL; j++) { printf("%4d", ar[i][j]); } printf("\n"); } #undef ROW #undef COL } int main() { Magic_Square_4K(); return 0; }
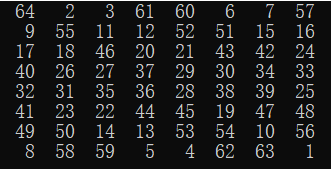
运行结果:
未完待续...
标签:位置 code efi 下标 直接 应该 pre add 顺序
原文地址:https://www.cnblogs.com/1651472192-wz/p/14640903.html